Es geht nach wie vor um zeitlich veränderliche elektrische und magnetische Felder. Dazu gehören auch die „Schwingungen”. Bei der nachfolgenden Betrachtung bewegen sich diese Schwingungen in einem Frequenzbereich, die niedrig genug sind, sodass die typischen Änderungszeiten in den betrachteten Systemen groß sind gegenüber den Ausbreitungszeiten der Felder in diesen Systemen.
Es liegen im Wesentlichen immer simultane Vorgänge vor, und die Schwingungen sind langsam genug, sodass sich die Felder nahezu gleichförmig über das ganze System ausbreiten. Wir bewegen uns zunächst nur im Bereich von 50-60 Hz. Wenn man sich dem Mega- oder Giga-Hz-Bereich annähert, gilt das Ganze nicht mehr, denn dann hat man es mit einer Wellenausbreitung zu tun.
Vorerst geht es um elektrotechnische Anwendungen basierend auf dem Ampere'schen Gesetz, dem Faraday'schen Induktionsgesetz und der Lorentz-Kraft. Das Induktionsgesetz hängt eng mit den Generatoren zusammen. Aber die Lorentzkraft ist dafür verantwortlich, dass sich Elektromotoren auch drehen.
Beim Wechselstrom geht es darum, dass es ein Magnetfeld gibt, hervorgerufen durch einen Permanentmagneten oder durch eine feste stromdurchflossene Spule. Sobald sich in dem Magnetfeld ein Leiterkreis bzw. eine Spule dreht, wird sich der magnetische Fluss durch diese Spule hindurch ändern. Und aufgrund dieser Änderung in der sich drehenden Spule wird schließlich eine Spannung induziert. Wenn nun noch ein Lastwiderstand angeschlossen wird, lassen sich Ströme erzeugen.
Also, durch eine sich drehende Spule entstehen Wechselspannungen und damit der Wechselstrom. Deshalb spricht man in diesem Zusammenhang von „zeitabhängigen” Spannungen.
Am besten lässt sich die „Wechselspannung” mit einer Sinus- oder Cosinus-Funktion beschreiben:

Wenn man an die spannungsführenden Klemmen einen Lastwiderstand anlegt, wird im Allgemeinen ein phasenverschobener Wechselstrom fließen. Wie es zu dieser Phasenverschiebung kommt, werden wir im nächsten Kapitel betrachten.
Generell gilt für den sich daraus ergebenden Strom:

U₀, I₀ sind die Amplituden
φ ist die Phasenverschiebung
ω ist die Kreisfrequenz
Wir erinnern uns aus der Mechanik, dass die Frequenz definiert ist als:
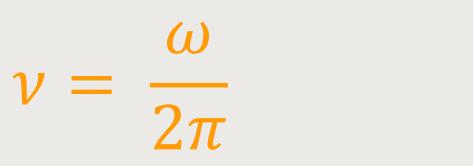
Und diese Frequenz beträgt in Europa 50 Hz und in Amerika 60 Hz. Das entspricht einer Periodenlänge von 20 ms.
Für die Periode gilt:
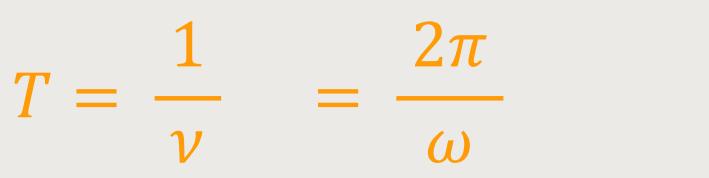
Wichtig ist natürlich in diesem Zusammenhang, was für eine „Stromleistung” sich daraus ergibt.
Generell gilt für die Leistung:

Da diese Leistung aber zeitabhängig ist, bezeichnet man sie auch als die „Momentanleistung”, die sich periodisch ändert.
Wenn man in obige Beziehung entsprechend einsetzt erhält man:

Da eine wechselnde Leistung bei der Berechnung äußerst ungünstig ist, betrachtet man lieber den Mittelwert und ist mehr an der Wirkleistung < P > interessiert. Hierzu wird über eine Periode gemittelt, sodass man erhält:
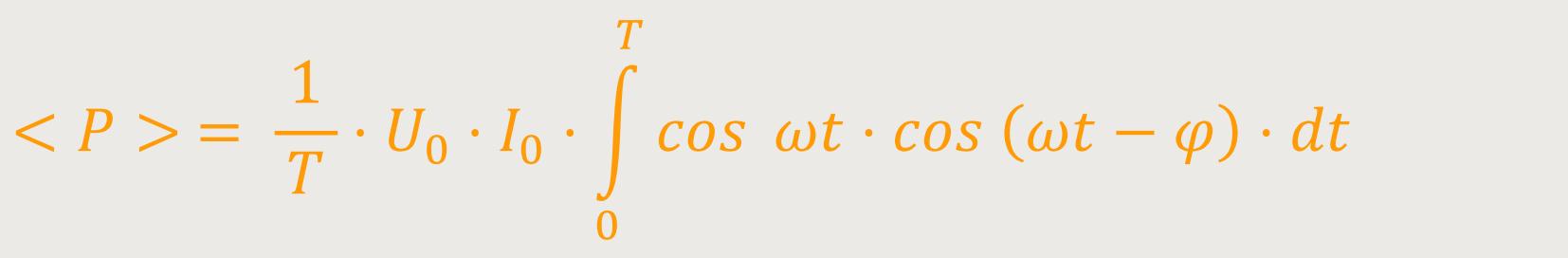
Wenn man dieses Integral ausrechnen möchte, muss man Substituieren. Unter Verwendung von Integraltafeln erhält man schließlich für die Wirkleistung:
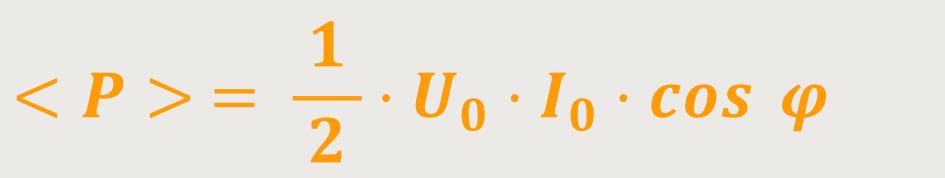
Grafik (wird später eingefügt)
In der Wechselstromtechnik spielen noch zwei weitere Größen eine Rolle.
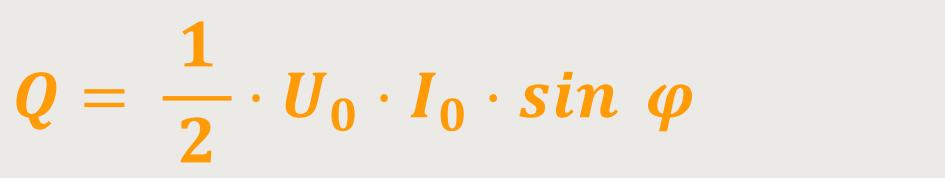
Diese Gleichung ist mit der obigen vergleichbar, nur dass statt des Cosinus jetzt der Sinus eingesetzt wird.
Unter der „Scheinleistung” versteht man, dass es so scheint, als ob in dem System diese Leistung umgesetzt wird. Aber es ist nur dann der Fall, wenn es keine Phasenverschiebung gibt. Hat man dagegen eine Phasenverschiebung, dann ist die wirklich umgesetzte Leistung kleiner als die Scheinleistung. Daraus ergibt sich:
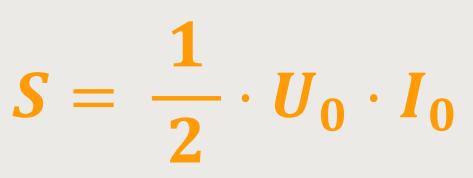
Beispiel: Bei einer Phasenverschiebung von
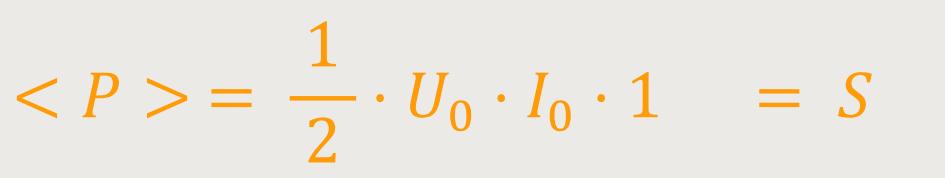
Q = 0
Jetzt möchte man eine Möglichkeit schaffen, bei der Berechnung der Leistung ähnlich vorzugehen, wie man es aus den Gleichstromkreisen her kennt.
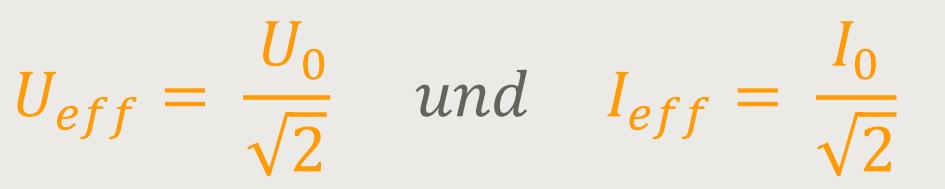
Wenn eine Wechselspannung vorliegt, entspricht U₀ der Amplitude. Dann definiert man sich eine Größe, die diese Spannung beschreibt, und das ist der „Effektivwert”. Das Gleiche wendet man auch beim Wechselstrom an.
Wenn man das entsprechend einsetzt, erhält man einen neuen Ausdruck für die Wirkleistung:

Diese Darstellung ist eine gängige Festlegung. Denn jedes Wechselstrom- und Wechselspannungsmessgerät zeigen immer die Effektivwerte an. Um den Wert der Amplituden zu erhalten, müssen die Effektivwerte mit √2 multipliziert werden. Das gilt aber alles nur für eine Phasenverschiebung von φ = 0°, was bei gängigen Lastwiderständen auch der Fall ist.
Bei einer Phasenverschiebung von φ = 90° bzw. π /2 ergibt sich für die Wirkleistung:
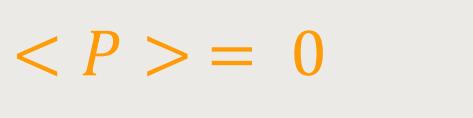
Für die Blindleistung und die Scheinleistung ergibt sich:
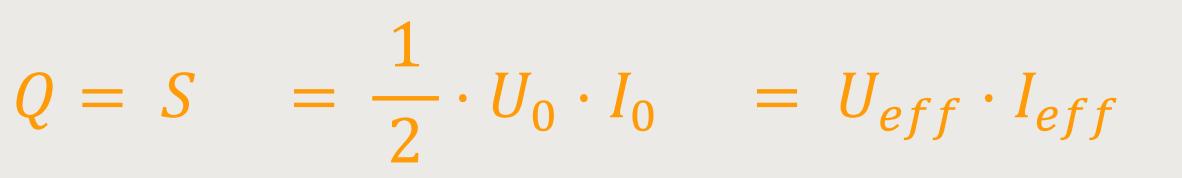
Das bedeutet, dass im Mittel keine Leistung umgesetzt wird, aber dennoch ein Wechselstrom fließt.
In der Praxis zeigt sich, dass es zum Erzeugen von Strömen oft günstiger ist, nicht nur eine Spule in einem Magnetfeld zu drehen und damit einen Wechsel der induzierten Spannung zu erreichen. Sondern man benutzt vielmehr einen Generator, der aus drei Induktionsspulen besteht und deren Achsen jeweils um 120° versetzt angeordnet sind.
Eine solche Anordnung von drei Spulen lässt man sich in einem äußeren homogenen Magnetfeld drehen. Und von jeder dieser Spulen wird dann die entsprechende Induktionsspannung abgegriffen. Daraus resultieren letztlich drei Induktionsspannungen, die aufgrund ihrer Winkellage eine entsprechende Phasenverschiebung von 120° aufweisen. Eine derartige Anordnung ist bei Drehstrommotoren gebräuchlich.
Das bedeutet für die Spannung in diesen drei Spulen:
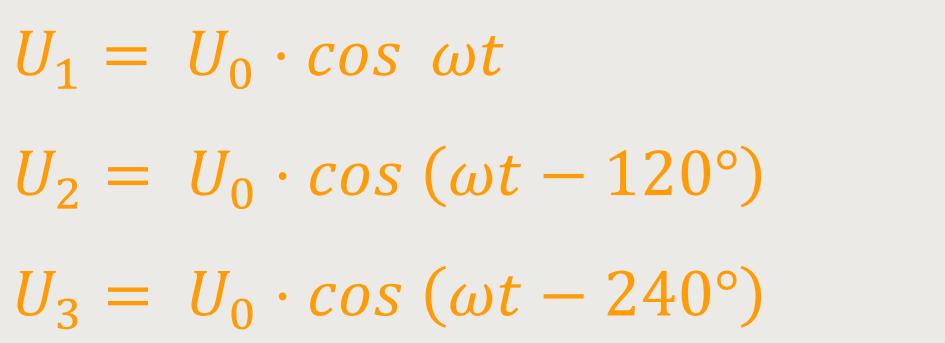
Grafik (wird später eingefügt)
Und für den Strom in den drei Spulen bedeutet das:

Diese Angaben der Phasenverschiebung sind nur dann zutreffend, wenn man im Wesentlichen gleichmäßige Ohm'sche Lastwiderstände hat und keine andersartigen Spulen oder Kondensatoren, die ihrerseits zu zusätzlichen Phasenverschiebungen führen können.
Grafik (Folie) (wird später eingefügt)
Bei einer derartigen Anordnung von 120°, und einer angelegten Spannung mit entsprechender Phasenverschiebung, wird in den Spulen ein Strom fließen, der als Summe des magnetischen Feldes ein sich drehendes magnetisches Feld hervorruft. Durch die Drehung des Magnetfeldes lassen sich letztlich mechanische Drehmomente übertragen.
Grafik (wird später eingefügt)
Sternschaltung ohne Phasenverschiebung ...
Im Null-Leiter fließt bei gleichen Ohm'schen Lastwiderständen kein Strom.
Grafik(wird später eingefügt)
Bei der Dreieckschaltung, muss man bei den Spannungen an den Verbraucherwiderständen Vorsicht walten lassen, weil diese hier nicht am Null-Leiter anliegen.

Ein solches Additionstheorem von Winkelfunktionen lässt sich verkürzt darstellen als:

Die √3 bedeutet, wenn die Einzelspannungen so gewählt werden, dass die Effektiv-Spannung Ueff ≅ 230 V beträgt und sich daraus die Spannung zwischen zwei Phasen ergibt:

Also, zwischen Null-Leiter und einer Phase beträgt die Effektiv-Spannung ca. 230 Volt, und zwischen zwei Phasen bei entsprechender Phasenverschiebung ergeben sich ca. 400 Volt.
Eine weitere wichtige Anwendung ist der „Transformator”.
Grafik (wird später eingefügt)
Beim Transformator hat man einen Eisenkern, an dem auf der einen Seite eine Primärspule und auf der anderen Seite eine Sekundärspule angeordnet ist. Die Primärspule wird an eine Wechselspannung U₁ angeschlossen. An der zunächst offenen Seite der Sekundärspule liegt eine Wechselspannung U₂. Beide Spulen können durchaus unterschiedliche Windungszahlen N₁ und N₂ haben.
In dem Primärkreis liegt kein Ohm'scher Widerstand, also kein Verbraucher. Wenn in der Primärspule ein Wechselfeld entsteht, gibt es einen zeitlich veränderlichen magnetischen Fluss, der dann eine entsprechende Sekundärspannung bewirkt.
Für die Primärspannung gilt:

In einem geschlossenen Primärkreis gilt für die Primärspule:
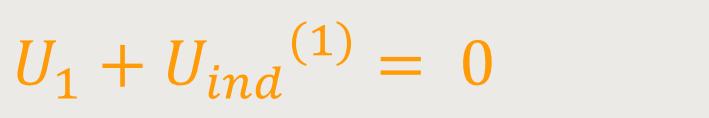
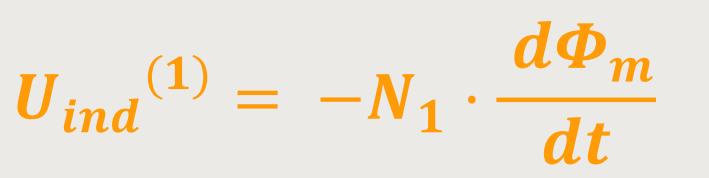
Wenn man entsprechend einsetzt und die Beziehung umstellt, ergibt sich:
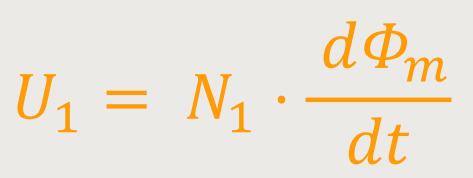
Somit hängt der magnetische Fluss Φm in dem Eisenkern ausschließlich mit der angelegten Primärspannung U₁ zusammen. Und er hängt damit von dem Magnetisierungsstrom Im in der Primärspule ab.
Und wie wirken die beiden Spannungen in den beiden Spulen zusammen?
Laut Induktionsgesetz gilt für die Primärspule (s.o.):
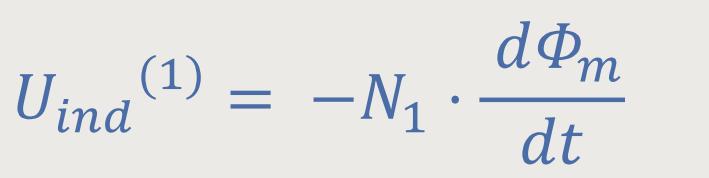
Da der magnetische Fluss durch den geschlossenen Eisenkern rundherum wirkt, gilt entsprechend für die Sekundärspule:
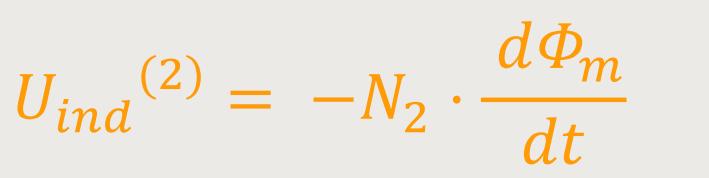
Damit ergibt sich für beide Spulen:
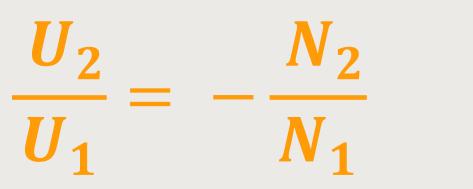
Und das ist die berühmte Transformatorgleichung.
Das Vorzeichen bei den Windungen hat keine besondere Bedeutung, weil es nur den Windungssinn der entsprechenden Spulen widerspiegelt.
Wenn die Sekundärspule zum Beispiel eine viel höhere Windungszahl hat, wird auch eine viel größere Spannung an der Sekundärspule auftreten, und umgekehrt gilt das genauso.
⇦ Kapitel Kapitel ⇨
