Die Elektro­dynamik und die Magneto­statik sind so sehr mit ein­ander verflochten, dass gerecht­fertigt erscheint, von einer elektro­magnetischen Wechsel­wirkung zu sprechen. Natür­lich sind die elek­trischen und die magne­tischen Aspekte nicht identisch. Aber dennoch sind sie durch gegen­seitige Beein­flussung so sehr miteinander verbunden, dass es nicht zweckmäßig wäre, diese als etwas Separates anzu­sehen. Mittler­weile ist es sogar so, dass auch die schwache Wechsel­wirkung zur elektro­magne­tischen mit hinzu­gefügt und zusammen­gefasst wurde zur elektroschwachen Kraft.

Im vorherigen Kapitel hatten wir das Ampere'sche Gesetz erarbeitet. Dem werden wir noch einmal kurz das Gauß'sche Gesetz gegen­über­stellen.

Wir erinnern uns, es lautete:

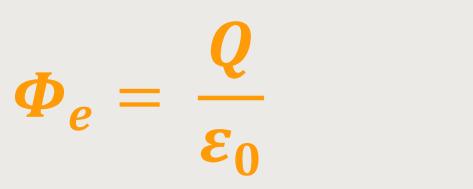
Dieses Gesetz besagt, dass der elek­trische Fluss aus einer geschlossenen Fläche heraus erfolgt, bei der sich inner­halb der Fläche eine Ladung Q befindet.

Grafik (wird später eingefügt)

Dem wurde das Amper'sche Gesetz gegen­über­gestellt:

Hier wird ausgesagt, dass eine magne­tische Spannung ein Linien­integral über ein entspre­chendes Vektor­feld der magne­tischen Fluss­dichte ist.

Grafik (wird später eingefügt)

Es geht also um eine geschlossene Kurve, durch die hindurch ein Strom I fließt. Und diese Kurve umschließt die bewegte Ladung. Im Grunde umgibt sich der Strom­fluss mit einem Feld­wirbel.

Wenn man jetzt beide Beziehungen gegen­über­stellt, erkennt man, dass die jeweilige Geometrie völlig anders ist. Es ist zum Beispiel nicht so, dass ein Strom ein Magnet­feld erzeugt. Das Magnet­feld quillt nicht heraus, sondern dieses Feld entsteht rundherum. Der Strom umgibt sich einfach damit, und das ist ein ganz wichtiger Unter­schied. In dem einen Fall ist in einer geschlossen Fläche etwas enthalten, aus der etwas heraus­tritt. Im anderen Fall tritt durch eine geschlossene Kurve etwas hindurch.

Jetzt möchten wir aber das Ampere'sche Gesetz in eine differen­tielle Form bringen. Und um zu dieser differen­tiellen Darstel­lung zu gelangen, ist es natürlich gut, von dem Strom I auf die Strom­dichte über­gehen zu können. Ähnlich wie man bei dem Gauß'schen Gesetz von der Ladung auf die Ladungs­dichte über­gegangen ist:

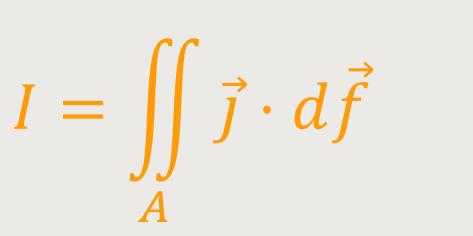
Grafik (wird später eingefügt)

Jetzt geht es darum, einen Zusammen­hang zwischen den Strom­dichte­vektoren und dem Vektor­feld des Magnet­feldes, das durch diesen Strom hervor­gerufen wird, darzu­stellen.

Wenn man obige Beziehung entspre­chend einsetzt, erhält man:

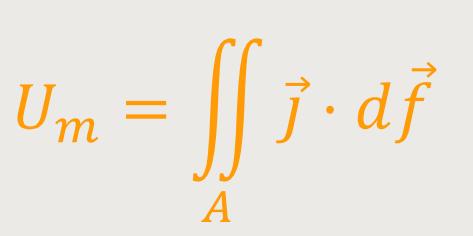
Und die magnetische Spannung war definiert als:

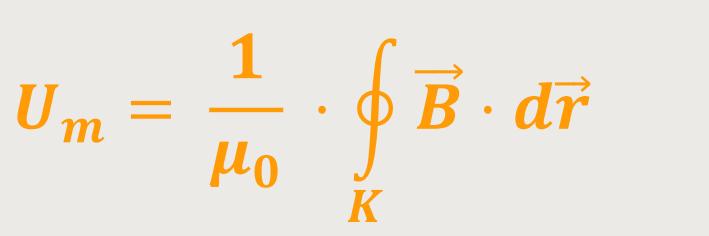
K   ist der Rand der Querschnitts­fläche (Rd (A) )

Doch um bei diesen Über­legungen weiter zu kommen, benötigt man einen Integral­satz. Das ist in diesem Fall der Stokes'sche Integralsatz:

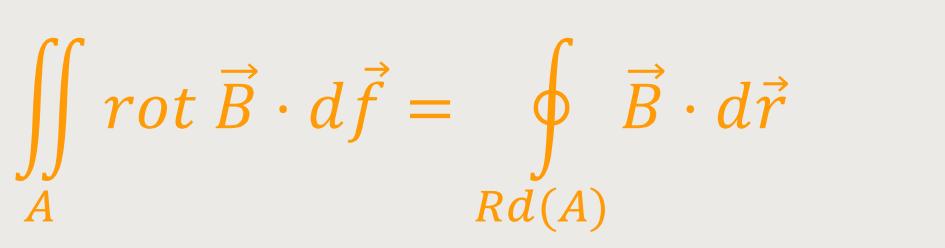
Im Grunde ist das nichts anderes, als der Gauß'sche Satz in einer anderen Dimension.

Durch diese Vorgehens­weise möchte man sich Arbeit ersparen. Denn ein Flächen­integral muss man zweimal integrieren. Ein Linien­integral dagegen nur einmal. Doch hier werden wir genau anders herum vorgehen, weil wir im weiteren Verlauf das Flächen­integral benötigen.

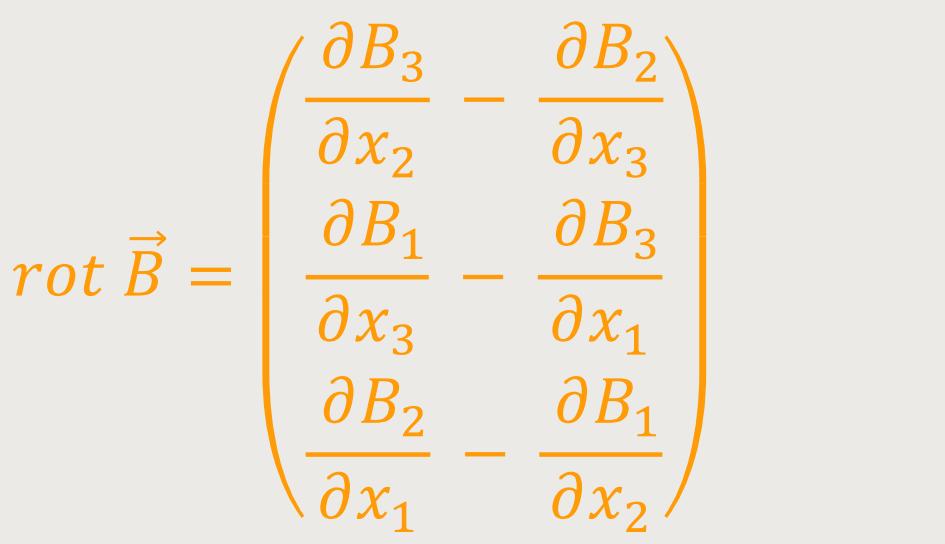
Eine Rotation ist nichts Geheimnis­volles, es ist lediglich ein Vektor. Wenn man ein Vektor­feld betrachtet, zum Beispiel das Vektor­feld der magne­tischen Fluss­dichte, dann wird es durch drei Komponenten B_₁, B_₂, B_₃ beschrieben, die jeweils eine Orts­funktion sind. Und nun erstellt man entspre­chend dieser Vorschrift die partiellen Ablei­tungen, und erhält damit den Vektor mit den obigen drei Kompo­nenten. Als Ergebnis erhält man den Vektor für die Rotation.

Mit dieser geschickten Umfor­mung lässt sich die magne­tische Spannung neu formulieren.

Auf Grundlage des Stokes'schen Satzes ergibt sich:

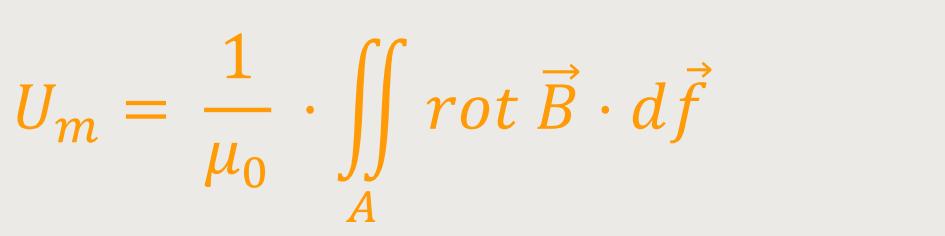
Jetzt haben wir zwei Formu­lierungen für die magnetische Spannung erhalten, die man nun gleichsetzten kann:

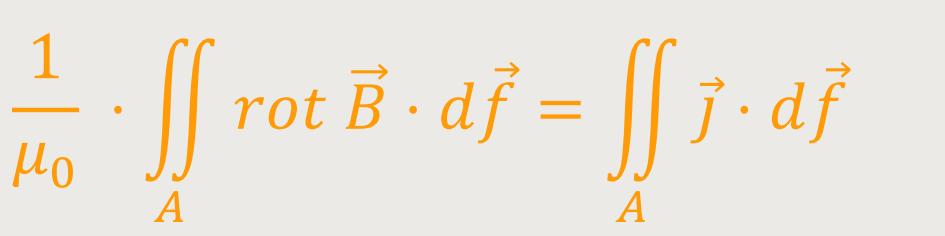
In beiden Fällen betrachtet man ein Flächen­integral über die gleiche Fläche, und das gilt unab­hängig der Gestaltung der Fläche. Wenn das aber für alle belie­bigen Flächen gelten soll, müssen auch die Integranden gleiches aussagen. Da dies hier der Fall ist, kann man diese entspre­chend gleich­setzen:

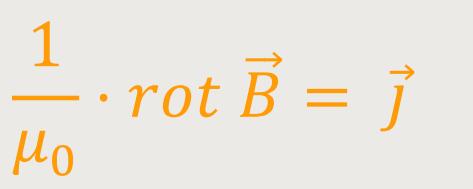
Das bedeutet für das Vektor­feld:

Und das ist die zweite Maxwell-Gleichung.

Diese Gleichung ist das Gegen­stück zur bereits erarbeiteten ersten Maxwell-Gleichung:

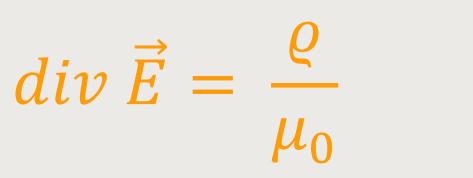
Jetzt haben wir etwas Entspre­chendes für die Magneto­statik erhalten. Dabei handelt es sich um eine weitere inhomogene Maxwell-Gleichung. Inhomogen bedeutet, dass auf der rechten Seite nicht Null steht.

Die zwei noch verblei­benden Maxwell-Gleichungen sind dagegen homogene Gleichungen. Das heißt, die Ladungs­dichten und die Strom­dichten, die in einem System vorherrschen, kommen nur in zwei Maxwell-Gleichungen vor. Und die bestimmen im Wesent­lichen, was mit den Feldern passiert. Denn wenn keine Ladungen und keine Ströme vorhanden sind, und damit alles statisch bzw. Null ist, dann wird sich auch kein Feld ausbilden.

Allerdings, wenn man zeit­lich veränder­liche elektro­magnetische Felder betrachtet, kann sehr wohl der Fall eintreten, dass selbst wenn und ϱ gleich Null sind, sich trotzdem ein Feld aufbaut, welches sich entspre­chend ausbreitet. Also, eine elektro­magnetische Welle kann sich auch in einem Bereich ausbreiten, in welchem es weder elek­trische Ladungen noch elek­trische Ströme gibt. Und das insbe­sondere auch im Vakuum.

Allerdings muss hier noch erwähnt werden, dass obige zweite Maxwell-Gleichung zunächst nur auf statische Systeme zutrifft. Wenn man zeit­liche veränder­liche Felder betrachtet, kommt noch ein weiterer Term hinzu.

Wir möchten den Stokes'schen Satz noch einmal anwenden, aber diesmal für eine kleine Fläche ΔA. Wenn eine Fläche klein genug gewählt wird, sodass sich das Vektor­feld nicht mehr gravierend ändert, dann ist die Funktion relativ konstant. Und dann lässt sich diese Fläche vor das Integral setzen und man erhält damit:

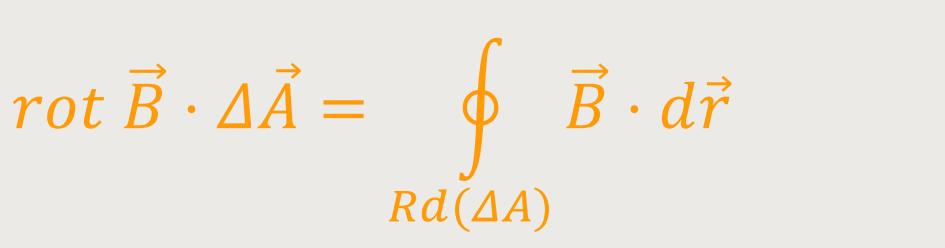
Was auf der rechten Seite steht, ist nichts anderes als die Zirku­lation des Feldes um die Fläche ΔA herum.

Und wenn voraus­gesetzt wird, dass ΔA || rot , dann lässt sich das betrags­mäßig mit der linken Seite gleich­setzen:

Durch Austausch des Terms ergibt sich schließlich:

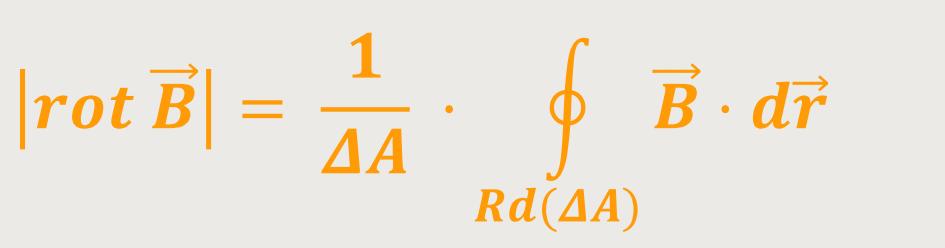
Und damit ist der Betrag von rot gleich­bedeutend mit der Zirku­lation um die Fläche ΔA herum pro Flächen­einheit.

Hierbei betrachtet man eine Fläche maximaler Zirku­lation. Und das nennt man auch die „Wirbel­dichte”. Es muss also die Fläche so gelegt werden, dass sie senkrecht auf rot steht, und das ander­seits der Flächen­vektor parallel zur rot steht.

Wenn man also einen magne­tischen Feld­wirbel betrachtet, mit welchem sich der Strom­fluss umgibt, dann wird der Vektor rot senkrecht auf eine Fläche stehen, um die herum die Zirku­lation maximal ist.

Grafik (wird später eingefügt)

Insofern ist rot ist ein Vektor, der die Achsen­richtung des Wirbels angibt. Je stärker der Strom fließt, desto größer werden die -Vekto­ren betrags­mäßig. Und desto größer wird auch die Zirku­lation pro Flächen­einheit.

Diese Maxwell-Gleichung sagt im Wesent­lichen aus, zumindest wenn man sie skalar inter­pretiert, dass die elek­trische Strom­dichte gleich der Wirbel­dichte des magne­tischen Feldes ist.

Der „magne­tische Fluss” lässt sich analog zum elek­trischen Fluss darstellen:

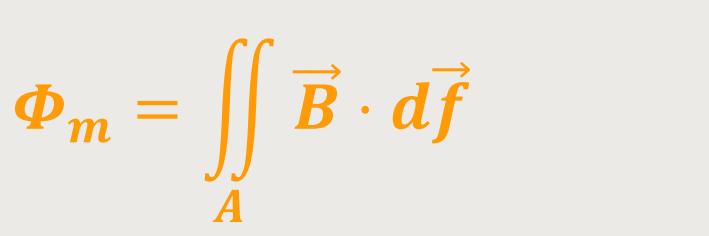
Und man erkennt, dass die magne­tische Fluss­dichte ist.

Die Dimension ist:

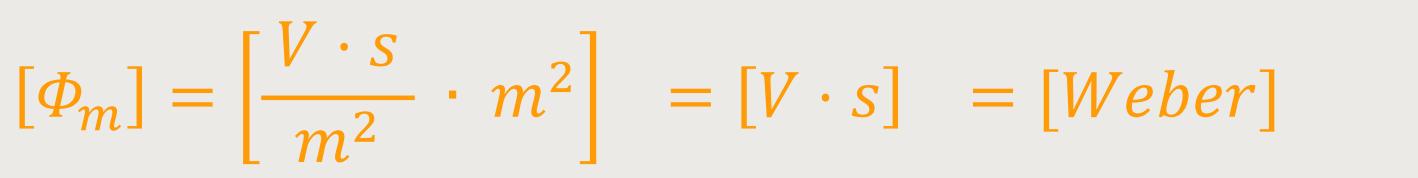
Den magne­tischen Fluss bezeichnet man auch gerne als die „Polstärke”.

Aufgrund dieser Definition kann man eine wesent­liche Schluss­folgerung ziehen. Nämlich, die Feld­wirbel deuten an, dass es sich stets um lauter geschlossene magne­tische Feld­linien handelt. Des Weiteren erkannt man, dass niemals aus irgen­deinem Raum­bereich nach allen Seiten hin ein Magnet­feld austritt. Denn sonst wäre es ja ein Monopol.

Der magne­tische Fluss aus einer geschlossenen Fläche heraus ist somit stets Null, und daraus folgt:

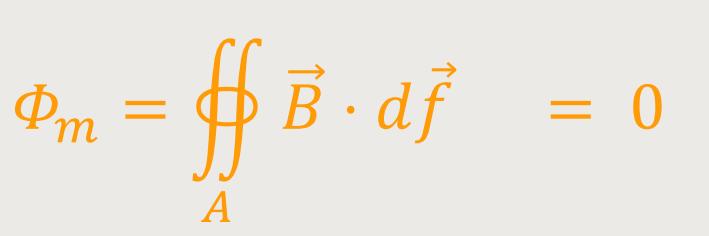
Dieser Fluss lässt sich laut Gauß'schen Satz umformen in ein Volumen­integral:

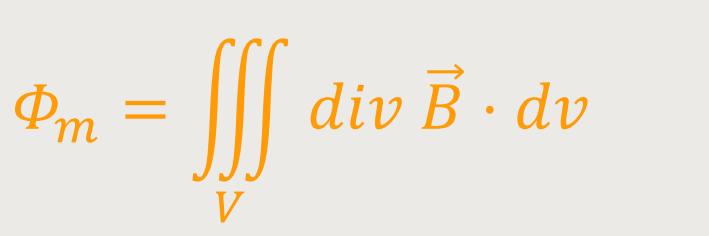
Und wenn der Wert bei jedem beliebigen Volumen gleich Null ist, folgt daraus abschlie­ßend:

Und das ist die dritte Maxwell-Gleichung.

Diese Gleichung ist aller­dings, wie bereits oben erwähnt, homogen. Das -Feld ist stets quell­frei. Das bestätigt noch­mals, dass es keine magne­tischen Monopole gibt.

⇦ Kapitel Kapitel ⇨