Wenn ein magnetischer Fluss durch eine Leiter­schleife zeitlich veränder­lich ist, dann wird in dieser Leiter­schleife eine Spannung induziert.

Daraus ergibt sich das Faraday'sche Induktionsgesetz:

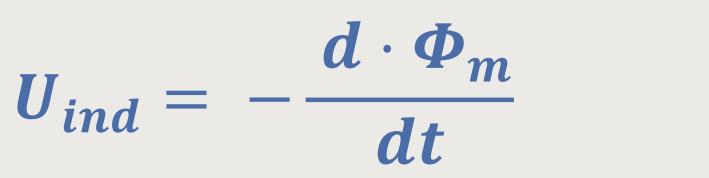
Hierbei steht das Verständnis dieses Gesetzes im Vorder­grund. Das ϕ_m ist der magne­tische Fluss durch die Fläche, die von einer Leiter­schleife umschlossen wird. Die induzierte Spannung entspricht der Spannung längs dieser Leiter­schleife. Wenn also der magne­tische Fluss durch eine Leiter­schleife, oder bei mehreren Schleifen durch eine Spule hindurch, sich zeitlich ändert, wird längs dieser Schleife(n) eine Spannung induziert.

Das negative Vorzeichen hängt mit der Lenz'schen Regel zusammen welche besagt, dass die induzierte Spannung so gerichtet ist, dass sie zu einer Behinderung des induzie­renden Vorgangs führt.

Wenn man obiges Ring­integral längs der geschlossenen Leiter­schleife dem magne­tischen Fluss gegen­über­stellt, lässt sich damit eine differen­tielle Gesetz­mäßig­keit ableiten. Es geht dann einzig und allein nur um die partielle Abhängig­keit mit der Zeit und nicht um die Orts­koordinaten, was sich wie folgt darstellt:

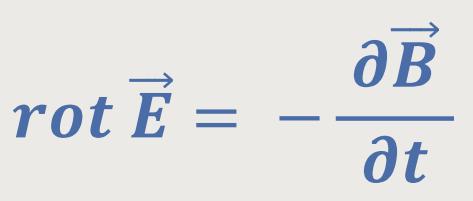
Eine solche zeit­liche Änderung des -Feldes führt zu einem elek­trischen Wirbelfeld.

Jetzt möchten wir noch kurz zwei Aspekte gegen­über­stellen.

In der Elektro­statik ging es nur um ruhende Ladungen, die ein elek­trisches Feld erzeugen. Bei ruhenden Ladungen sprechen wir von konstanten Feldern ohne Zeit­abhängig­keiten. Das heißt, ein elektro­statisches Feld ist wirbelfrei. In diesem Fall gibt es auch keine geschlossenen Feld­linien. Und damit handelt es sich um ein konser­vatives Feld.

Weil keine Zeit­abhängig­keit vorhanden ist, ergibt sich daraus eine wesent­liche Erkenntnis:

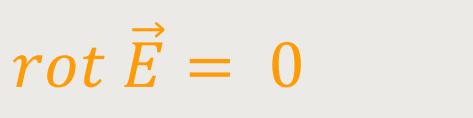
Daher lässt sich das elek­trisches Feld als Gradient darstellen:

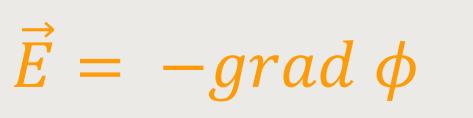
Und wenn man einen solchen Potential­ansatz macht, lässt sich die Spannung, die ja wie nach­folgend definiert ist, auch als Potential­differenz darstellen:

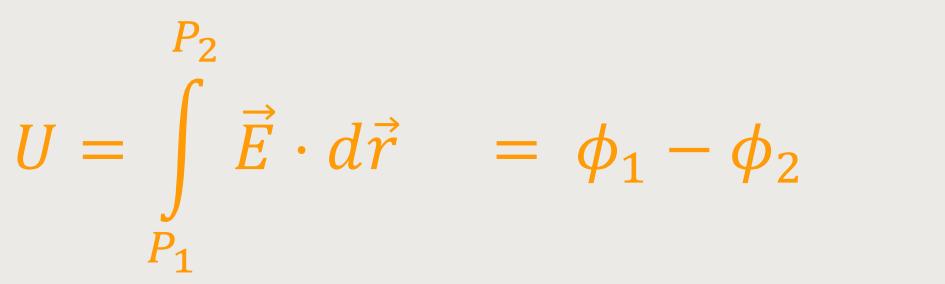
Diese Definition wurde bereits in der Elektro­statik behandelt.

Wenn jetzt aber eine zeitlich veränder­liche Situation vorliegt, nämlich ein zeitlich veränder­liches magne­tisches Feld, dann ist rot ≠ Null. In diesem Fall gibt es geschlossene -Linien. Und damit ist es ein nichtkonservatives elektrisches Feld. Daher ist das Integral ∫ · d wegabhängig. Somit lässt sich das elek­trische Feld nicht mehr darstellen als:

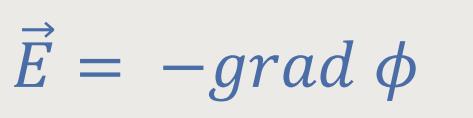
Die Spannung in der Elektro­dynamik lässt sich nicht mehr als Potential­differenz darstellen, sondern es gilt nur noch:

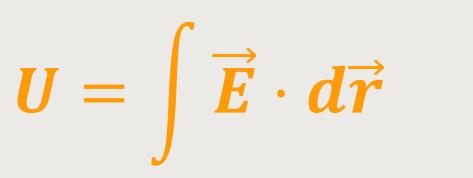
Der Strom, der sich in einer Leiter­schleife aufgrund einer induzierten Spannung ausbildet ist so gerichtet, dass dieses aus dem Strom resul­tierende Magnet­feld die Bewegung eines Permanent­magneten behindern möchte. Diese Behinderung ist auf die Wechsel­wirkungs­kräfte zurückzuführen.

(Inhalt folgt später.)

Als typisches Beispiel kann man sich zwei neben­einander angeordnete Spulen anschauen. Die eine von den beiden nennt man die „Feldspule”. Durch diese Feldspule fließt ein gewisser Strom I ⁽¹⁾, der von einer Wechsel­spannungs­quelle erzeugt wird. Als Folge davon wird durch diese Spule ein magne­tisches Feld erzeugt. Dieses Feld wird zum Teil auch die zweite Spule durch­setzen.

Wird an der zweiten Spule ein Voltmeter ange­schlossen, lässt sich dort die induzierte Spannung U_ind ⁽²⁾ messen. Denn wenn ein zeit­lich veränder­licher Strom durch die Feld­spule fließt, führt dies auch zu einem zeit­lich veränder­lichen Magnet­feld, und zu einem zeit­lich veränderlichen magne­tischen Fluss durch die zweite Spule. Die Folge ist, dass in der zweiten Spule eine Spannung induziert wird. Deshalb nennt man diese Spule auch die „Induktionsspule”.

Bei einer derartigen Spulenanordnung gelten einfache Beziehungen:

Somit ist der Strom durch die Feldspule proportional zum magne­tischen Fluss durch die Induktions­spule. Man spricht hier auch von der gegen­seitigen Induk­tivität. Die Induk­tivität bezeichnet man mit L und ist quasi ein „Propor­tionalitäts­faktor”:

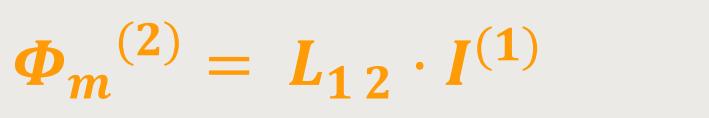
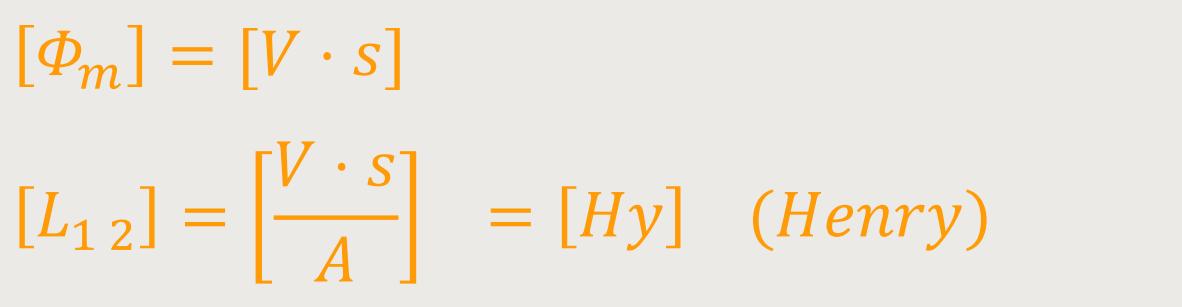
Gemäß dem Faraday'schen Induktions­gesetz lässt sich nun die induzierte Spannung in der zweiten Spule ermitteln:

Wenn der Propor­tionalitäts­faktor zeitunab­hängig bleibt, erhält man bei der Differentiation:

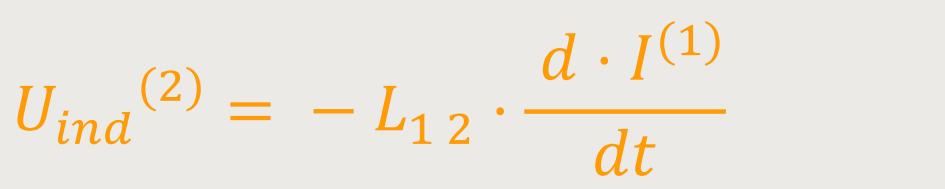
Diese Beziehung beschreibt die zeitliche Veränderung des Stromes durch die Feldspule.

Grafik (wird später eingefügt)

Diese Effekte zeigen sich nicht, solange man nur statische Situationen betrachtet. Sie werden erst sichtbar, wenn eine zeit­liche Abhängig­keit mit einfließt.

Wie lässt sich nun eine derartige gegenseitige Induktivität ausrechnen?

Nehmen wir zum Beispiel zwei ineinander gewickelte zylindrische Spulen. Wir gehen zunächst davon aus, dass beide Spulen die gleiche Länge und auch den gleichen Durch­messer haben. Des Weiteren besitzen beide Spulen den gleichen Kern und sie haben auch die gleiche Querschnitts­fläche:

n⁽¹⁾, n⁽²⁾   ist die Windungsdichte der Spule

Der Betrag der magnetischen Flussdichte im Innern der Feldspule beträgt:

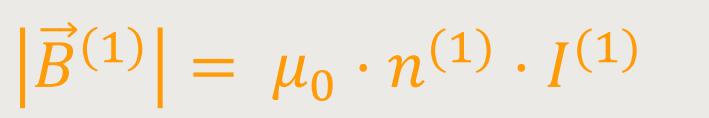
n   ist die Anzahl der Windungen pro Längeneinheit (Feldspule u. Induktionsspule)

Damit ergibt sich der Fluss, der durch eine Windung der zweiten Spule, sprich der Induktions­spule, hindurch­tritt.

Für den magne­tischen Fluss durch eine Windung der Induktions­spule gilt:

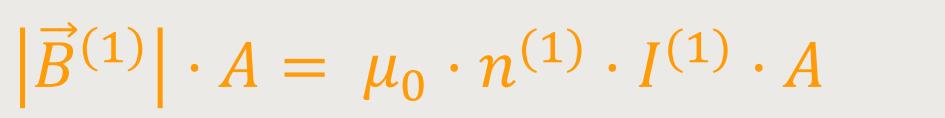
A   ist die gemeinsame Querschnitts­fläche

Für den Fluss durch alle Windungen der Induktions­spule gilt:

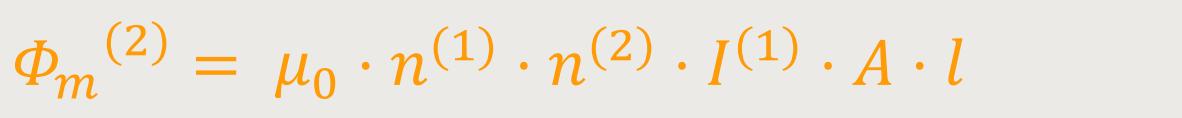
A · l   ist das Spulen­volumen

l   ist die gemeinsame Länge der beiden Spulen

Oder als „Induktivität” ausgedrückt, lässt sich auch schreiben:

Somit lässt sich die „gegen­seitige” Induk­tivität sehr leicht ermitteln, wenn die Spulen­windungs­dichte und das Spulen­volumen bekannt sind. Aufgrund dieses Spezial­falls lässt sich auch schluss­folgern was passiert, wenn man nur eine Leiter­anordnung betrachtet.

Wenn man jetzt nur durch eine Spule einen Wechsel­strom fließen lässt, wird sich bei einer Ände­rung des Stromes auch eine Ände­rung des magne­tischen Flusses ergeben. Aber dieser magne­tische Fluss führt seiner­seits in derselben Spule zu einer Induktions­spannung. In diesem Fall wird die Induktions­spannung der induzie­renden Ursache, also dem ursprüng­lich fließenden Strom entgegen­wirken und diesen quasi bremsen. Diesen Effekt nennt man auch die „Selbst­induk­tivität”.

In diesem Fall gilt, wie bereits oben beschrieben:

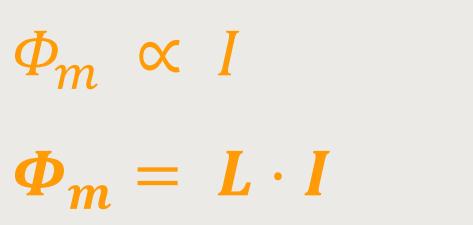
Der Propor­tionalitäts­faktor wird auch hier wieder mit L bezeichnet. Wobei damit jetzt die Selbst­induk­tivität bezeichnet wird. Diese Spule wirkt in der Weise auf sich selbst zurück, dass sich eine Induktions­spannung ergibt.

Nach dem Induktionsgesetz gilt auch hier:

Und wenn auch hier der Propor­tionalitäts­faktor wieder zeitunab­hängig bleibt, erhält man bei der Differentiation:

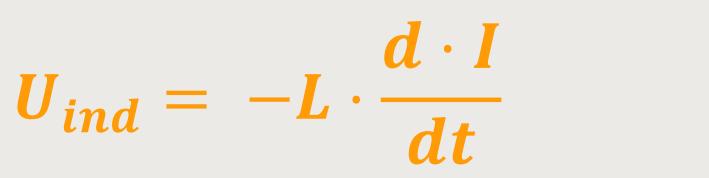
Das negative Vorzeichen sagt wieder aus, dass aufgrund der Induktions­spannung eine Behinderung des induzie­renden Vorgangs, sprich des Stromaufbaus, erfolgt. Denn der Strom­aufbau führt zum Feld­aufbau, also zu einer Änderung des magne­tischen Flusses und damit zu einer Induktions­wirkung. Diese Wirkung führt letzten Endes zu einer Zeit­verzöge­rung des fließenden Stromes.

Wenn sich ein elek­trisches Wirbel­feld aufgrund eines veränder­lichen magne­tischen Flusses ausbildet, hat dieses Wirbel­feld auf die Spule selbst, dort wo dieser Strom fließt, eine entspre­chende Auswirkung. Dadurch ergibt sich eine Rück­wirkung des Systems auf sich selbst.

Die Selbst­induk­tivität lässt sich wie folgt ausdrücken:

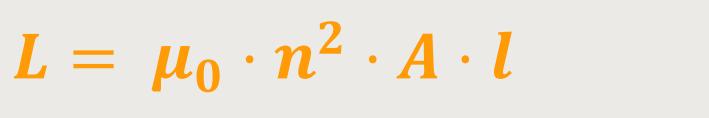
n   ist die Windungs­dichte der Spule
l    ist die Länge der Spule
A   ist die Querschnitts­fläche

Der zeitlich veränder­liche magne­tische Fluss in der Feld­spule führt zu einer Induktions­wirkung in derselben, wodurch diese Feldspule auch als „Induktions­spule” aufzufassen ist. Die Ausprägung der Selbst­induk­tivität wirkt sich somit quadratisch mit der Windungs­zahl aus. Denn sowohl die Wirkung auf den magne­tischen Fluss, als auch die Induktions­wirkung auf die Spule selbst, nimmt zu.

Man sieht also, aufgrund der Lenz'schen Regel kommt es zu einer Behinde­rung der induzie­renden Ursache, sprich zu einem verzögerten Strom­aufbau. Diese Wider­spenstig­keit macht sich insbesondere bei Schalt­vorgängen in den elek­trischen Spulen bemerkbar.

⇦ Kapitel Kapitel ⇨