Hierbei betrachten wir die Massenanziehung zweier Massenpunkte bei großen Systemen (z.B. Erde-Mond bzw. Erde-Sonne).

Bei der Gravitationskraft ist die Kraft immer proportional zur Masse.

Die Wechsel­wirkungs­kraft zwischen zwei Massen­punkten (m_₁ , m_₂ ) kann demnach wie folgt definiert werden:

Wenn zwei Massen­punkte gleich­berechtigt einander gegen­über stehen, dann muss aus Symmetrie­gründen auch gelten, dass die Wechsel­wirkungs­kraft eben­falls propor­tional sein muss.

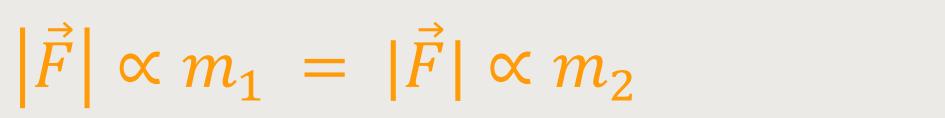
Das hat auch etwas mit Aktio und Reaktio zu tun. Das „Reaktions­prinzip” sagt ja im Wesent­lichen aus:

Der Betrag der Kraft auf die eine Masse ist gleich dem Betrag der Kraft auf die andere Masse.

Die Massen sind im Grunde nur entgegen­gerichtet. Doch wie hängt diese Kraft­wirkung vom Abstand zwischen diesen beiden Punkt­massen ab? Newtons Idee war es, diese beiden Massen von ihrer Distanz abhängig zu machen.

Hierzu hat Newton die Mond­umlauf­bahn beobachtet. Er hat also das System Erde-Mond betrachtet, zwei Massen­punkte, genügend weit vonein­ander entfernt. Dabei konzen­trierte er sich auf einen Mond­umlauf. Die Distanz zwischen Erde und Mond konnte man schon zu Newtons Zeiten durch trigono­metrische Vermessungen ermitteln. Wenn man an ausreichend weit entfernten Punkten auf der Erde gleich­zeitig den Mond anvisiert, wird das nicht parallel sein. Durch die Winkel kann man auf den Radius der Mond­bahn schließen. Außer­dem wusste man damals schon recht gut, wie groß der Radius der Erde ist.

Der Erdradius beträgt: R = 6370 × 10³ m
Radius der Mondbahn: R_M ≅ 60 R = 382.200 km

Die Zeitdauer für einen Mond­umlauf um die Erde (siderischer Monat) entspricht: T_M = 27,32 Tage.

Zum Vergleich beträgt der synodische Monat: 29,5 Tage.

Des Weiteren fragte sich Newton, wie kommt es denn, dass der Mond auf seiner Umlauf­bahn um die Erde bleibt? Er kam zu dem Schluss, dass auch der Mond unter dem Ein­fluss der Schwer­kraft stehen muss.

Wenn man weiß, wie groß die Umlauf­zeit ist, dann kennt man auch seine Winkel­geschwindig­keit ω² r, und damit erhält man den Betrag der „Zentri­petal­beschleuni­gung”. Die Zentri­petal­beschleunigung kommt dadurch zustande, dass Erde und Mond einander anziehen. Also erhält man dadurch auch gleich die dortige Fall­beschleuni­gung. Der Mond fällt faktisch um die Erde herum. Seine Zentri­petal­beschleunigung ist gleich der Fall­beschleuni­gung von der Erde aus bewirkt, aber an der Stelle des Mondes.

Die Fallbeschleunigung bzw. die Zentri­petal­beschleuni­gung an der Stelle Mondes ist definiert als:

Die Winkel­geschwindig­keit des Mondes ist der Winkel, der pro Zeit­einheit über­schritten wird. Hierzu nimmt man den vollen Winkel und dividiert ihn durch die Umlaufzeit.

Jetzt kennen wir ja bereits die Fall­beschleuni­gung an der Erdober­fläche:

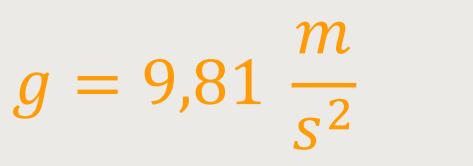
Da man aber nur mit Massen­punkten rechnen möchte, lässt sich die Fall­beschleuni­gung, die eigent­lich nur in der Nähe der Erdober­fläche wirkt und deren Wirkung so beschreiben, als wäre die Masse der Erde im Zentrum vereinigt. Und dann wäre die Distanz, also der Erd­radius, gleich R.

Damit haben wir die Fall­beschleuni­gung im Abstand von R und 60 R.

Das Verhältnis der beiden Radien beträgt 1/3600. Um diesen Wert ändert sich die Fall­beschleuni­gung, genau gesagt um einen quadratischen Wert. Wenn man in den 60-fachen Abstand geht, wird die Fall­beschleuni­gung um 1/60² zurückgehen.

Dadurch ergibt sich allein durch astrono­mische Beobachtungen, dass der Betrag der Kraft definiert ist als:

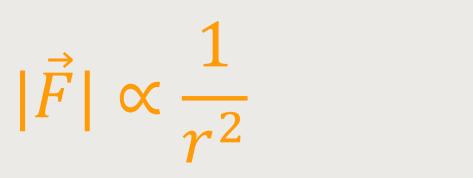
r   ist der Abstand der beiden Punktmassen

Damit erhalten wir das berühmte Newton'sche Gravitations­gesetz:

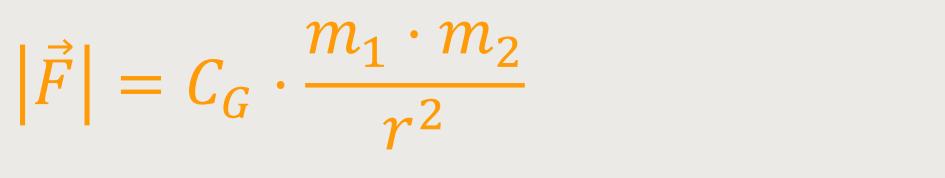
C_G   ist die Gravitations­konstante

Hinweis:
Eine völlig analoge Beziehung gilt auch für die elektro­statische Wechsel­wirkung zweier Punkt­ladungen. Es handelt sich dabei aber nicht um dieselbe Kraft wie oben beschrieben. Das sind grund­sätzlich völlig unter­schiedliche Kräfte. Was sich schon daran zeigt, dass die elektro­statischen und allgemein die elektro­dynamischen Kräfte von elektrischen Ladungen abhängig sind. Und wenn man einen Körper entlädt, gibt es die Kraft nicht mehr. Entladen kann man einen Körper zwar, aber Entmassen kann man einen Körper nicht.

Außerdem gilt das Äquivalenz­prinzip nur für die Gravitations­kraft. Warum das trotzdem so ähnlich ausschaut, hängt einfach mit der Geometrie zusammen. Wenn man zwei punkt­förmige Körper betrachtet, wird ihre Wechsel­wirkung mit 1/r² beschrieben. Das ist ähnlich einfach, wie wenn man eine punkt­förmige Licht­quelle hat. Die Bestrahlungs­intensität geht zurück, und zwar mit zuneh­mendem Abstand proportional zu 1/r². Wenn man auf die doppelte Entfernung geht, dann wird die Bestrahlung von der Punkt­licht­quelle auch auf 1/r² zurückgehen.

Allerdings hat Newton obiges Gesetz nie so aufge­schrieben. Er hat nämlich diese Konstante nicht mit berück­sichtigt. Sie war zu seiner Zeit noch nicht bekannt und selbst bis heute lässt sich diese Konstante nicht ausrechnen. Man hat sie bisher nur messen können (siehe Cavendish-Versuch). Das ist im Grunde die schlechteste bekannte universelle Konstante, die es in der Physik gibt.

Der Bestwert für diese Konstante beträgt:

Dieser Wert der Gravitations­konstante bedeutet:

Wenn man zwei Punkt­massen betrachtet, die sich im Abstand von 1 m befinden, wo jede die Masse von 100 to hat, dann wird die Anziehungs­kraft ca. 1 N sein.

Nach bisherigem Verständnis sind dies die einzig ordnenden Kräfte im Universum.

Jetzt wollen wir das Gravitations­gesetz noch in eine vektorielle Form bringen. Dabei gilt zu berück­sichtigen, dass sich Massen einander immer anziehen. Massen stoßen sich nie ab.

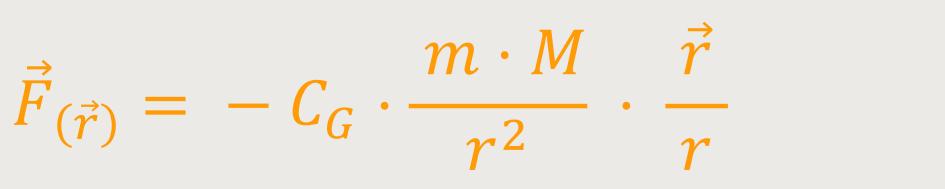
M   steht hier für die Sonne
m   ist hierbei die Erde
  ist der Abstand der Punktmassen
/r   ist der Einheitsvektor, der auch als () bezeichnet wird
C_G   ist die Gravitationskonstante

Auf diese Weise lässt sich das Kraft­feld vektoriell aufschreiben:

Der Ursprung O liegt bei der Masse M. Der Orts­vektor ist der Abstand der beiden Punkt­massen. Dieser Orts­vektor zeigt immer von der feld­erzeugenden Masse hin zur Probe­masse. Aber die Kraft ₍₎, die auf die Probe­masse wirkt zeigt, weil es eine anziehende Kraft ist, wieder in Richtung der feld­erzeugenden Masse. Und weil diese Kraft entgegen­gesetzt gerichtet ist, erhält sie ein negatives Vorzeichen.

⇦ Kapitel Kapitel ⇨