Der „Minkowski-Raum” ist benannt nach Hermann Minkowski (1864-1909), der sich dem Studium der Mathe­matik und Physik gewidmet hat. Bei diesem Raum handelt es sich um einen 4-dimen­sionalen Raum, in welchem sich die Relativitäts­theorie elegant formu­lieren lässt. Um das Jahr 1907 erkannte Minkowski, dass die Arbeiten von Hendrik A. Lorentz (1904) und Albert Einstein (1905) zum Thema „Relativitäts­theorie” in einem nicht-euklidischen Raum verstanden werden können. Minkowski vermutete, dass Raum und Zeit in einem 4-dimen­sionalen Raum-Zeit-Kontinuum mit­einander verbunden sind.

Drei der Koordinaten des Minkowski-Raums sind die klassischen des Eukli­dischen Raums. Hinzu kommt eine vierte Koordinate für die Zeit. Der Minkowski-Raum ist also analog wie ein 4-dimen­sionaler eukli­discher Raum aufgebaut. Doch wegen der unter­schied­lichen Struktur von Raum- und Zeit­koordinaten unter­scheiden sich beide Räume voneinander.

Der Minkowski-Raum kann als 4-dimen­sionaler reeller Vektor­raum aufgefasst werden, in welchem das Skalar­produkt nicht durch den üblichen Ausdruck, sondern durch eine sogenannte nicht­ausgeartete „Bilinear­form” vom Index 1 gegeben ist.

Als Bilinear­form bezeichnet man in der linearen Algebra eine Funktion, die zwei unabhän­gigen Vektoren einen Skalar­wert zuordnet und die linear in ihren beiden Argumenten ist. Insofern ist diese Bilinear­form nicht positiv definiert. Hierbei ordnet man den Minkowski-Vektoren (vier an der Zahl), man spricht auch von Ereig­nissen, 4-kompo­nentige Elemente x bzw. y zu. Folgende Regel ist gebräuchlich:

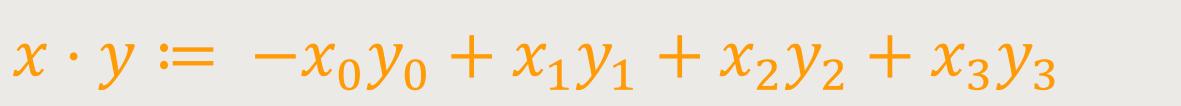
Die Koordinate x₀ = c · t geht mittels der Licht­geschwin­dig­keit c aus der Zeit­komponente t hervor.

In der Allgemeinen Relativitäts­theorie wird all­gemein obige Signatur (−,+,+,+) verwendet. Eine physikalisch äquivalente umgekehrte Signatur (+,−,−,−) ist in der Teil­chen­physik weit verbreitet. Die Zeit wird manch­mal auch als vierte (x₄ y₄) statt als nullte Koordinate geführt.

Alternativ kann man das innere Produkt zweier Elemente des Minkowski-Raums auch als Wirkung des metrischen Tensors η_μν auffassen:

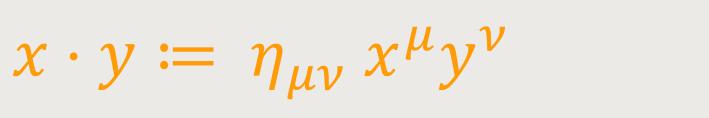
In der oben dargestellten Tensor-Schreib­weise unter­scheidet man zwischen kontra­varianten (Indizes oben) und kovarianten (Indizes unten) Vektor­komponenten.

Ein 4-dimen­sionaler Raum mit Minkowski-Metrik wird definiert als:

(Der Abstand zweier Vierer-Vektoren r₁ und r₂ im Minkowski-Raum ist damit gegeben durch:

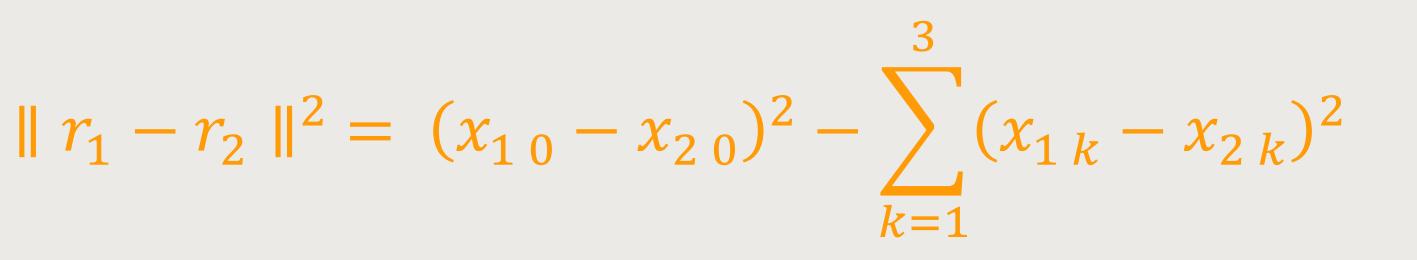
Die inhomogene Lorentz­gruppe lässt den Vierer-Abstand invariant; sie umfasst die räum­lichen und zeit­lichen Trans­lationen und Spiege­lungen sowie die Trans­formationen der homogenen Lorentz­gruppe.

Abb. 1: Der Minkowski-Raum

Aufgrund der Lorentz-Trans­formation lässt sich erkennen, dass die Zeit­koordinate mit einbe­zogen werden muss, weil sich die Zeit beim Trans­formieren auch ändert. Deswegen muss die Zeit in den grafischen Darstel­lungen mit berück­sichtigt werden. Und dem­entspre­chend bewegt man sich in einem 4-dimen­sionalen Raum.

Minkowski hatte basierend auf den Arbeiten von Lorentz und Einstein die Idee, Raum und Zeit nicht mehr als zwei separate physika­lische Einheiten zu sehen, sondern beide in einem Modell zu vereinigen.

Minkowski unter­teilte seine Argumen­tation in 5 Abschnitte, in welchen er schritt­weise ausführte, wie man von der gegen­wärtig ange­nommenen Mechanik allein durch rein mathe­matische Über­legungen zu verän­derten Ideen über Raum und Zeit kommen könnte. Zunächst bezog sich Minkowski auf die Gleichungen der Newton'schen Mechanik und deren zwei­facher Invarianz (Unver­änder­lich­keit). Zum einen bleibt deren Forma­lismus erhalten, selbst wenn man das zugrunde gelegte räum­liche Koordinaten­system einer beliebigen Lage­verän­derung unter­zieht. Selbst wenn man seinen Bewegungs­zustand verändert, indem man ihm irgend­eine gleich­förmige Trans­lation aufprägt. Und selbst der Null­punkt der Zeit spielt hierbei keine Rolle.

Um das graphisch zu veran­schau­lichen, wählte er, wie wir es auch heute noch gewohnt sind, x, y, z als recht­winklige Koordi­naten für einen gedachten Raum. Für die Zeit wird t gewählt. Gemäß unserer Wahr­nehmung sind Ort und Zeit stets mit­einander ver­bunden. Niemand betrachtet einen Ort los­gelöst von der Zeit oder anders herum, wenn­gleich beide Begriffe eine unter­schied­liche Bedeutung haben.

In unserem Beispiel soll ein Raum­punkt, der einem Werte­system, bestehend aus x, y, z, t ent­spricht, im weiteren Verlauf „Weltpunkt” genannt werden. Die Gesamt­heit aller denkbaren Werte­systeme x, y, z, t soll dementspre­chend „Welt” heißen.

Der Raum unserer Anschauung soll zudem kein Vakuum aufweisen, sodass an allen Orten und zu jeder Zeit etwas wahr­genommen werden kann. Minkowski wählte dafür nicht den Begriff „Materie” oder „Elektrizität”, sondern wählte bewusst den Begriff „Substanz”.

Einem Zeitpunkt dt sollen die Ände­rungen dx, dy, dz der Raum­koordi­naten dieses substan­ziellen Punktes ent­sprechen. Als Abbild beschreibt dieser substan­zielle Punkt einen Kurven­verlauf bzw. eine Welt­linie, deren Punkte sich ein­deutig auf den Parameter t von −∞ bis +∞ beziehen lassen. Die ganze gedachte „Welt” lässt sich in der­artige Welt­linien auf­lösen, wobei zwischen den einzelnen Welt­linien die Gesetze der Physik und deren Wechsel­wirkungen zu beobachten sind.

Durch die Begriffe „Raum” und „Zeit” fallen die x, y, z-Mög­lich­keiten bezogen auf t = 0 und ihre zwei Gegen­sätze t > 0 und t < 0 auseinander. Bestimmt man den Null­punkt von Raum und Zeit, so bedeutet das für die Trans­forma­tionen der Mechanik, dass die x, y, z-Achsen zum Zeit­punkt t = 0 beliebig um den Null­punkt gedreht werden dürfen.

Daraus ergeben sich zwei durch den Punkt t = 0 getrennte Schalen, in Anlehnung eines zweischaligen Hyper­boloids. Zunächst betrach­ten wir die in positive Richtung zeigende Schale im Bereich t > 0. Außer­dem werden jetzt die homogenen linearen Trans­forma­tionen von x, y, z, t in vier neue Variable mit der Bezeich­nung x', y', z', t' über­tragen, wobei der Ausdruck dieser Schale in den neuen Variablen entspre­chend wird. Zu diesen Trans­forma­tionen gehören offenbar die Drehungen des Raums um den Null­punkt.

Zu den vorge­nannten Trans­forma­tionen sollen nun noch beliebige Verschie­bungen des Raum-Zeit-Null­punktes hinzu­gefügt werden. Dadurch erhalten wir graphisch eine von dem Parameter c abhängige Gruppe von Trans­forma­tionen, die Minkowski mit G_c bezeichnete.

Um Missverständ­nisse auszuräumen, legte Minkowski fest, um welchen Wert es sich bei dem Para­meter c handelt. Für c soll die Licht­geschwin­dig­keit im Vakuum voraus­gesetzt werden, in welchem ledig­lich die elektro­magne­tischen Wechsel­wirkungen zum Tragen kommen. Die Unveränder­lich­keit der Natur­gesetze soll daher für die Gruppe G_c gelten.

Auf Grund­lage aller Natur­erschei­nungen kann durch konse­quente Annähe­rung ein Bezugs­system x, y, z, t als Raum-Zeit-Kontinuum abgeleitet werden, welches den Gesetzen der Natur folgt. Hierbei ist das Bezugs­system jedoch nicht durch die Erschei­nungen ein­deutig fest­gelegt. Dement­spre­chend hielt Minkowski folgendes fest:
Das Bezugs­system lässt sich je nach Trans­forma­tion der Gruppe G_c beliebig verändern, ohne Einfluss auf die Natur­gesetze zu nehmen.

Minkowski schloss den ersten Teil mit den Worten ab, dass auf diese Weise die 3-dimen­sionale Geometrie ein Kapitel der 4-dimen­sionalen Physik wird.

Nun erhebt sich die Frage, welche Umstände uns eine veränderte Sicht von Raum und Zeit aufzwingen? Denn wenn die neue Sicht­weise den Natur­erschei­nungen nicht wider­spricht, eröffnet sich die Möglich­keit, Beziehungen ein­deutig zu definieren. Bevor Minkowski darauf einging, stellte er eine wichtige Bemerkung voran.

Wenn Raum und Zeit eine Erwei­terung erfahren haben, so ent­spricht einem ruhenden substan­ziellen Punkt als Welt­linie eine zur t-Achse parallele Gerade. Handelt es sich dagegen um einen gleich­förmig bewegten substan­ziellen Punkt, so ist es eine gegen die t-Achse geneigte Gerade. Und wenn es schließ­lich um einen ungleich­förmig bewegten substan­ziellen Punkt geht, ist die Welt­linie irgendwie gekrümmt.

Hierzu führte Minkowski folgendes Axiom ein:
Die in einem beliebigen Welt­punkt vorhandene Substanz kann stets bei geeigneter Fest­setzung von Raum und Zeit als ruhend auf­gefasst werden.

Das Axiom besagt, dass in jedem Welt­punkt stets der Ausdruck

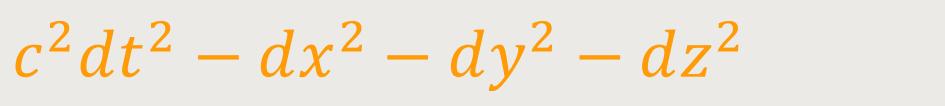
... Gültig­keit hat. Oder mit anderen Worten, jede Geschwin­dig­keit v ist stets kleiner als die Licht­geschwin­dig­keit c. Bezogen auf alle substan­ziellen Geschwin­dig­keiten würde c als obere Grenze bestehen und hierin die tiefe Bedeutung der Größe c liegen.

Minkowski schluss­folgerte, dass wenn man beispiels­weise die Gruppe G_c betrachtet und es gäbe es starre Körper, man erkennen könnte, dass durch die zwei zu den beiden Gruppen G_c und G_∞ gehörenden hyper­boloidischen Schalen nur „eine” t-Richtung verläuft. Und das würde als Konsequenz bedeuten, dass man an geeig­neten starren optischen Instrumenten eine Verän­derung der Erscheinungen bei unter­schied­licher Ausrichtung gegen die Rotations­richtung der Erde wahr­nehmen müsste.

Nach Lorentz soll jeder Körper, der in Bewegung ist, in Richtung der Bewegung eine Verkür­zung erfahren, und zwar bei einer Geschwin­dig­keit v im Verhältnis

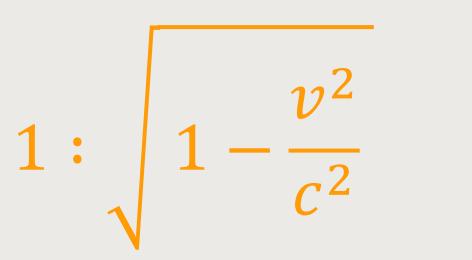
Diese Hypothese klang für Minkowski äußerst phantastisch. Denn die Kontraktion sei nicht eine Folge von Wider­ständen im Äther, so wie man sich das All ursprünglich vorstellte, sondern ein Glücks­fall, quasi als Begleit­umstand der Bewegung zu sehen.

Minkowski wollte nun an einer Grafik veranschau­lichen, dass die Hypothese von Lorentz völlig äquivalent mit Einsteins Aufsatz über die Auffassung von Raum und Zeit ist, wodurch sie viel verständ­licher wird.

Der Einfach­heit halber trennen wir die Dimen­sionen y und z gedank­lich ab, und denken uns nur mehr eine räum­lich 1-dimensionale Welt. Daraus ergibt sich ein entsprechend der t-Achse aufrechter und ein gegen die t-Achse geneigter Parallel­streifen (siehe Abb. 2). Die Dar­stellung spiegelt den Verlauf eines ruhenden, bezüg­lich eines gleich­förmig bewegten Körpers wider, der jedes Mal eine konstante räum­liche Ausdehnung behält.

Lorentz bezeichnete in seiner Abhand­lung die Verbindung t' von x und t als Orts­zeit des gleich­förmig bewegten Elektrons und benutze eine physika­lische Konstruktion dieses Begriffs zum besseren Verständnis der Kontraktions­hypothese. Jedoch zu erkennen, dass die Zeit des einen betrachteten Elektrons dem des anderen gleicht, also t und t' gleich­zusetzen ist, sei erst ein Verdienst von A. Einstein gewesen.

Damit war der Begriff „Zeit” durch die Darstellungen als eine ein­deutige Größe fest­gelegt worden. An dem Begriff des „Raums” rüttelten weder Einstein noch Lorentz viel­leicht auch deshalb nicht, weil bei der oben ange­führten Trans­forma­tion, bei der die x', t'-Ebene sich mit der x, t-Ebene deckt. Was die Schluss­folgerung zulässt, als sei die x-Achse des Raums in ihrer Lage erhalten geblieben. Über den Begriff des „Raums” in entspre­chender Weise hinweg­zuschreiten, sei wohl nur als Verwegen­heit der mathe­matischen Kultur einzu­ordnen.

Nach dem nun zwingend not­wendigen erlangten Verständnis der Gruppe G_c erschien Minkowski das Wort „Relativitäts­postulat” für die Forderung einer Unveränder­lich­keit der Gruppe G_c nicht aus­reichend. Das würde dem Sinn nach bedeuten, dass durch die Erschei­nungen in Raum und Zeit nur eine 4-dimen­sionale Welt abge­bildet wird, aber die Projek­tion in Raum und in Zeit für sich noch mit einer gewissen Freiheit vor­genommen werden kann. Aus diesem Grund verwendete Minkowski lieber den Namen „Postulat der absoluten Welt” (oder kurz Weltpostulat).

Durch das neu definierte Welt­postulat wird es nach Minkowskis Ansicht möglich, die vier Bestimmungs­stücke x, y, z, t gleich zu behandeln.

Vor allem wird deutlich, was es mit dem Begriff Beschleu­nigung auf sich hat.

Minkowski bediente sich hierzu einer geome­trischen Ausdrucks­weise, die sich nach seinen Worten anbietet, wenn man im Tripel, also dort, wo die Koordinaten­punkte x, y, z zusammen­treffen, still­schweigend nur noch von dem Punkt z spricht. In diesen Punkt wird nun der Raum-Zeit-Null­punkt O gelegt.

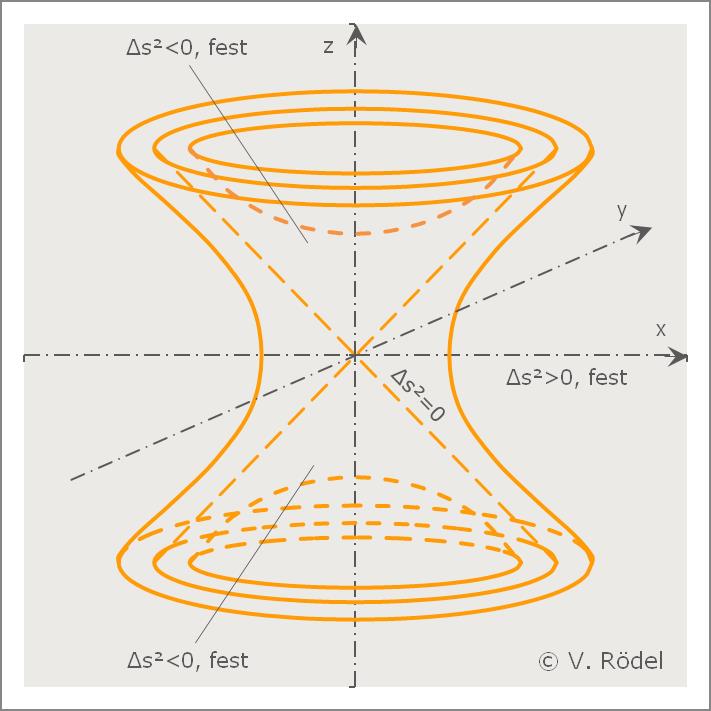
Der Kegel, definiert als

... und mit dem Punkt O als dessen Spitze (siehe Abb. 2), besteht aus zwei Teil­bereichen. Der eine Bereich mit den Werten Null­punkt t < 0, und der andere Bereich mit den Werten t > 0.

Abb. 3: Zeigt die von Minkowski skizzierten zwei Bereiche

Den ersten, uns zuge­wandten Bereich, hatte Minkowski als „Vor­kegel” bezeichnet, der aus allen Welt­punkten bestehen soll, die Licht „in Richtung O senden”. Der zweite, von uns weg­gewandte Bereich, bezeich­nete er als „Nach­kegel”, der seiner­seits aus allen Welt­punkten besteht, die Licht „von O aus­gehend” empfangen. Die vom Vor­kegel einge­grenzte Fläche bezeich­nete Minkowski als „dies­seits von O” und die Fläche des Nach­kegels als „jenseits von O”. Jenseits von O entspräche dann der weiter oben betrach­teten hyper­boloidischen Schale:

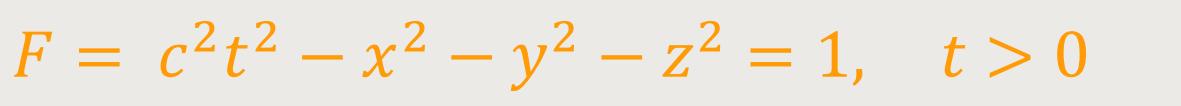
Der Bereich zwischen den Kegeln wird ein­gegrenzt von den ein­schaligen hyper­boloidischen Verläufen

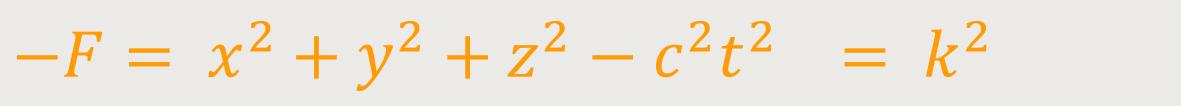
... und beinhaltet alle konstanten positiven Werte k².

Die einzelnen Äste dieser Hyperbeln werden zunächst als „Zwischen­hyperbeln zum Zentrum” O bezeichnet. Ein derartiger Hyperbelast würde, wenn er einer Welt­linie eines substan­ziellen Punktes entspräche, eine Bewegung wider­spiegeln, die für t = −∞ und t = +∞ sich asymptotisch der Licht­geschwin­dig­keit c annähert.

In Anlehnung an den klassischen Vektor­begriff in einem Raum soll jetzt eine definierte Strecke stell­vertretend für alle Möglich­keiten x, y, z, t als Vektor bezeichnet werden. Dabei wird aller­dings unter­schieden zwischen den zeit­artigen Vektoren, die vom Punkt O wegzeigen. Diese Vektoren zeigen in Richtung der Schale +F = 1, t > 0, und stehen für die Zeit. Die raum­artigen Vektoren zeigen in Richtung des Bereichs mit −F = 1, und stehen für den Raum. Die Zeit­achse an sich kann mit jedem Zeit­vektor parallel verlaufen. Jeder Welt­punkt, der zwischen dem Vor­kegel und dem Nach­kegel liegt, kann auf Grund­lage des Bezugs­systems ent­weder mit dem O-Punkt zusammen­fallen, oder früher als O bzw. später als O posi­tioniert werden. Damit ist dann ein­deutig definiert, ob sich ein Welt­punkt zeitlich vor oder nach dem O-Punkt befindet. Beim Grenz­über­gang c = ∞ würde es in diesem Fall zu einem voll­ständigen Zusammen­klappen des keil­förmigen Ein­schnitts zwischen den Kegeln kommen, was der „ebenen” Mannig­faltig­keit t = 0 ent­spricht.

Versetzten wir uns nun gedank­lich in einen solchen Welt­punkt P der durch seine Kompo­nenten x, y, z, t bestimmt ist, und die durch einen substan­ziellen Punkt verlaufende Welt­linie. Verfolgt man diesen Punkt auf seinem Weg, ergibt sich für den Betrag des zeit­artigen Vektor­elements dx, dy, dz, dt im weiteren Verlauf der Linie der Betrag:

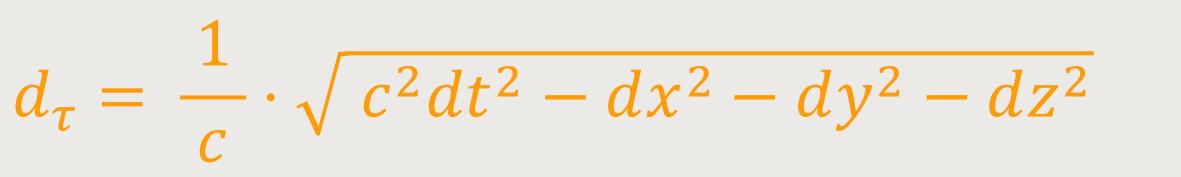
Minkowski wies auf die nachweis­baren Fort­schritte zum Thema „pondero­motorische Kraft” im elektro­magne­tischen Feld hin, welche sich auf die betrachtete Gruppe G_c über­tragen lassen. Unter der ponderomotorischen Kraft versteht man heute den nieder­frequenten Anteil der Kraft eines räum­lich inhomogenen, hoch­frequenten elektro­magne­tischen Feldes auf ein System von (sich in diesem Feld bewegenden) elek­trischen Ladungen.

Die damaligen Ansätze veranlassten Minkowski zu einer einfachen Regel:
Bei der Änderung des Bezugs­systems ist die voraus­gesetzte Kraft in der Weise als eine Kraft in den neuen Raum­koordinaten anzusetzen, dass dabei der zuge­hörige Vektor mit den Komponenten

... bei denen

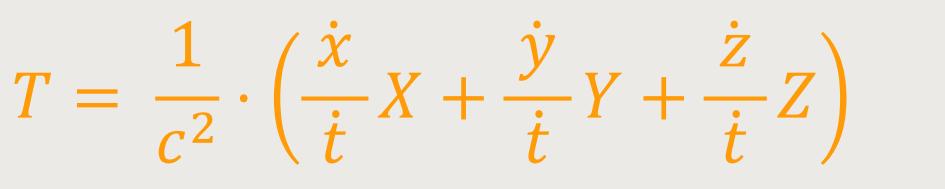
... die durch c² dividierte Arbeits­leistung der Kraft im Welt­punkt ist, unver­ändert bleibt.

Dieser Vektor ist stets normal zum Bewegungs­vektor im Punkt P. Ein solcher, zu einer Kraft im Punkt P gehörende Kraft­vektor, bezeichnete Minkowski als ein sich „bewegender Kraft­vektor im Punkt P”.

Im weiteren Verlauf soll die durch diesen Punkt P ver­laufende Welt­linie, die ja den substan­ziellen Punkt wider­spiegelt, mit konstanter mecha­nischer Masse m beschrieben werden. Das m-fache, des Bewegungs­vektors im Punkt P soll als der „Impuls­vektor in P” bezeichnet werden. Wogegen das m-fache, des Beschleu­nigungs­vektors im Punkt P als der „Kraft­vektor der Bewegung in P” bezeichnet werden soll.

Diese Definitionen beschreiben das Gesetz dafür, wie die Bewegung eines Massen­punktes bei gegebenem sich bewegenden Kraft­vektor statt­findet. Damit soll gelten:
Der Kraft­vektor der Bewegung ist gleich dem bewegenden Kraft­vektor.

Nach Minkowskis Ansicht, fasst diese Aussage die vier Gleichungen für die Komponenten nach den vier Achsen zusammen. Wobei die vierte Gleichung, weil von vorn­herein beide genannten Vektoren normal zum Bewegungs­vektor angeordnet sind, sich als eine Folge der drei ersten Gleichungen ansehen lässt. Nach der obigen Bedeutung von T stellt die vierte Gleichung zweifellos den Energie­satz dar. Als kinetische Energie des Massen­punktes ist daher der c²-fache der Kompo­nente des Impuls­vektors nach der t-Achse zu definieren.

Daraus ergibt sich die Beziehung:

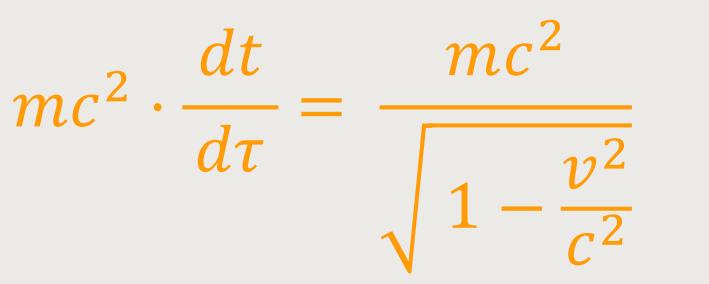
Das entspricht nach Abzug der additiven Konstante mc² dem Ausdruck ½ mv² der Newton'schen Mechanik bis auf die Größen von der Ordnung 1/c². Sehr anschau­lich erscheint hierbei die Abhängig­keit der Energie vom Bezugs­system. Da nun aber die t-Achse in die Richtung jedes zeit­artigen Vektors gelegt werden kann, enthält ander­seits der Energie­satz, für jedes mögliche Bezugs­system, bereits das ganze System der Bewegungs­gleichungen.

Diese Tatsache behält bei dem angespro­chenen Grenz­wert bei c = ∞ ihre Bedeutung auch für den Aufbau der Axiome der Newton'schen Mechanik, was bereits in solchem Sinn von J.R. Schütz (1897) fest­gestellt worden sei.

Nach Aussage von Minkowski lässt sich von vorn­herein das Verhältnis von Längen­einheit zu Zeit­einheit so wählen, dass dies der natür­lichen Geschwindig­keits­schranke c = 1 ent­spricht. Führt man dann die Beziehung (√-1) · t = s an Stelle von t ein, so erhält man folgenden quadra­tischen Differential­ausdruck:

Dadurch zeigt sich eine völlige Symmetrie in x, y, z, s, und diese Symmetrie ist auf jedes Gesetz über­tragbar, welches dem Welt­postulat nicht wider­spricht.

Die Vorteile, die sich aus dem Welt­postulat ergeben, werden durch nichts so treffend belegt, wie durch die Beschreibung des Verhaltens einer beliebig bewegten punkt­förmigen Ladung nach den in der Maxwell-Lorentzschen Theorie beschrie­benen Wechsel­wirkungen.

Laut Aussage von Minkowski fallen in einer Mechanik, die aufgrund obigen Welt­postulats über­arbeitet werden müsste, die Diskrepanzen zwischen der Newton'schen Mechanik und der modernen Elektro­dynamik von selbst weg.

Minkowski bewertete abschließend noch die Stellung des Newton'schen Attraktions­gesetzes, heute als „Gesetz der Gravitation” bekannt, in Bezug auf obiges Postulat. Er nahm an, wenn zwei Massen­punkte m, m₁ jeweils ihre Welt­linie beschreiben, würde von m auf m₁ ein in Bewegung befindlicher Kraft­vektor ausgeübt. Und zwar so, wie er zuvor in Verbindung mit den Elektronen beschrieben wurde, nur dass für −ee₁ jetzt +mm₁ eingesetzt wird.

Wir betrachten nun den speziellen Fall, dass der Beschleu­nigungs­vektor von m konstant Null ist, wobei wir anschlie­ßend t so einsetzen, dass m als ruhend auf­gefasst werden kann. Zusätz­lich erfolgt die Bewegung von m₁ allein durch den von m bewirkten Kraft­vektor. Nun wird dieser definierte Kraft­vektor zunächst durch Hinzufügen folgenden Faktors erweitert:

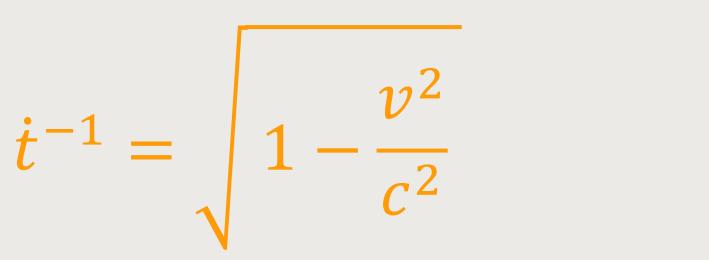
Bei Größen von der Ordnung von 1/c² auf 1 zeigt sich, dass für die Koordinaten x₁, y₁, z₁ von der Masse m₁ und deren zeit­lichen Verlauf genau wieder die Keplerschen Gesetze Anwendung finden. Aller­dings würden dabei an die Stelle der Zeiten t₁ die Eigen­zeiten τ₁ von m₁ treten. Auf­grund dieser ein­fachen Anmerkung kann man schnell erkennen, dass das vorge­schlagene Gravita­tions­gesetz verknüpft mit der über­arbeiteten Mechanik, nicht weniger gut geeignet ist, die astro­nomischen Beobachtungen zu erklären, genauso wie das Newton'sche Gravita­tions­gesetz verknüpft ist mit der Newton'schen Mechanik.

Die Gültig­keit obigen Welt­postulats ohne Einschrän­kungen ist, so war Minkowski davon über­zeugt, der wahre Kern eines elektro­magne­tischen Welt­bildes, der von Lorentz ersonnen, und von Einstein weiter ausgeführt wurde.

⇦ Kapitel Kapitel ⇨