Unter dem Begriff „Gravi­tation” versteht man auch gerne die „Massen­anziehung” oder all­gemein die „Gravitations­kraft”. Gegen­wärtig zählt man sie noch zu den vier Grund­kräften der Physik, wenng­leich sie eine Sonder­stellung ein­nimmt. Sie äußert sich nach dem weit­läufigen Verständnis in der gegen­seitigen Anziehung von Massen.

Die Gravita­tion nimmt mit zuneh­mender Entfernung der Massen vonein­ander ab. Sie soll aber unbe­grenzte Reich­weite haben, weil man sich sonst die Beobach­tungen im Universum nicht erklären kann. Im Gegen­satz zu den elektro­magne­tischen Kräften lässt sie sich nicht abschirmen.

Hier auf der Erde bewirkt die Gravitation, dass alle Körper nach „unten” fallen, sprich in Richtung Erdmittel­punkt, sofern sie nicht durch andere Kräfte daran gehindert werden. Nach bis­herigem Verständnis bestimmt die Gravi­tation in unserem Sonnen­system die Bahnen der Planeten, Monde, Satelliten und Kometen. Sie sei auch im Kosmos für die Entstehung von Galaxien und Sternen verant­wortlich.

Die Gravita­tion wird oft mit der Schwer­kraft gleich­gesetzt. Das Gewicht eines Körpers wird aller­dings vom lokal herrschenden Schwere­feld bestimmt, welches nicht nur die Gravitations­kraft beinhaltet, sondern auch die auf den Körper wirkenden Trägheits­kräfte. Letzteres ist dann der Fall, wenn das Bezugs­system rotiert.

Im Rahmen der klassischen Physik wird die Gravi­tation mit dem Newton'schen Gravitations­gesetz beschrieben. Es soll sich dabei um eine instantan durch den leeren Raum wirkende Fern­wirkungs­kraft handeln, also eine Kraft die ohne Verzögerung sofort ihre Wirkung zeigt.

Ein grundlegend anderes Verständnis der Gravita­tion ergibt sich aus der Allgemeinen Relativitäts­theorie (ART) nach Albert Einstein. Hierbei wirkt die Gravitation nicht in Form einer Kraft auf die Körper, sondern wird durch eine Krümmung der 4-dimensionalen Raum­zeit verursacht. Die Bahnen der Körper, auf die keine weiteren Kräfte wirken, beschreiben dann die lokal kürzeste Verbindungs­kurve zweier Punkte.

Interes­sant ist, wie sich das Verständnis der Gravita­tion über die Jahrhun­derte hinweg stetig verbessert hat. Und es spricht viel dafür, dass das gegen­wärtige Verständnis noch nicht der Weisheit letzter Schluss ist. Es folgt ein kurzer geschicht­licher Über­blick.

Der griechische Philosoph Aristoteles beschrieb in der Antike im Rahmen seiner Kosmo­logie die „Schwere” als eine Eigen­schaft der sublu­naren Elemente. Dazu zählten die Elemente Erde, Feuer, Wasser und Luft. Alle Körper, die aus diesen Elementen bestehen, würden dann zum Mittel­punkt der Erde streben. Diese Vorstel­lung war lange das physika­lische Haupt­argument für das geozen­trische Weltbild.

Altindische Autoren führten den freien Fall auf eine Kraft zurück, die propor­tional zur Masse eines Objektes ist und in Richtung des Erdmittel­punkts wirkt. Der persische Astronom Muhammad ibn Musa z. B. versuchte im 9. Jahr­hundert, die Bewe­gungen der Himmels­körper durch eine Art Anziehungs­kraft zu erklären.

Al-Biruni über­setzte im 11. Jahr­hundert verschie­dene Werke indischer Autoren ins Arabische und ins Persische. Sein Zeit­genosse Alhazen formu­lierte darauf­hin eine Theorie der Massen­anziehung.

Der Perser Al-Khazini stellte seiner­seits im 12. Jahr­hundert die Vermu­tung auf, dass die Stärke der Erdan­ziehung abhängig ist vom Abstand zum Erdmittel­punkt. Interessant ist, dass er bereits zwischen der Masse, dem Gewicht und der Kraft unter­schied, so wie es heute auch noch in der Physik üblich ist.

Ein bedeu­tender Kritiker der Physik des Aristoteles und Weg­bereiter des koperni­kanischen Welt­bildes ist der „Spätscholastiker” Nikolaus von Oresme. Er hielt im 14. Jahr­hundert die Erd­rotation für wahr­schein­lich und beschrieb die Möglich­keit vieler Welten sowie vieler gravita­tiver Zentren.^[1]
Das stand völlig im Wider­spruch zu einer ruhenden, im Mittel­punkt des Universums liegenden und alles Schwere anziehenden Erde. Diese Vorstellung vertrat nämlich die Kirche über viele Jahr­hunderte hinweg. Und wer eine andere Anschauung vertrat, musste um sein Leben fürchten.

Nikolaus Kopernikus ging 1543 in seinem Manus­kript (De revolu­tionibus orbium coelestium) davon aus, dass außer der Erde auch alle anderen Himmels­körper Gravita­tion ausüben. Er drückte es wie folgt aus:

„ ... Ich bin wenigs­tens der Ansicht, dass die Schwere nichts Anderes ist, als ein von der gött­lichen Vorsehung des Welten­meisters den Theilen einge­pflanztes, natürliches Streben, vermöge dessen sie dadurch, dass sie sich zur Form einer Kugel zusammen­schließen, ihre Ein­heit und Ganz­heit bilden. Und es ist anzu­nehmen, dass diese Neigung auch der Sonne, dem Monde und den übrigen Planeten innewohnt ...” ^[2]

Johannes Kepler veröffent­lichte 1609 in seiner Abhand­lung (Astronomia nova) folgende Axiome:^[3]

• Jede körper­liche Substanz ist, insofern sie körper­lich ist, von Natur aus dazu geneigt, an jedem Ort zu ruhen, an dem sie sich allein befindet, außer­halb des Kraft­bereichs eines verwandten Körpers.

• Die Schwere besteht in dem gegen­seitigen körper­lichen Bestreben zwischen verwandten Körpern nach Vereini­gung oder Verbindung (von dieser Ordnung ist auch die magne­tische Kraft), so dass die Erde viel mehr den Stein anzieht; als der Stein nach der Erde strebt.

• Das Schwere wird [...] nicht zum Welt­mittel­punkt als solchen hinge­trieben, sondern als den Mittel­punkt eines verwandten runden Körpers ...

• Wäre die Erde nicht rund, so würde das Schwere nicht über­all gerad­linig auf den Mittel­punkt der Erde zu, sondern von verschie­denen Seiten aus nach verschie­denen Punkten hinge­trieben.

• Wenn man zwei Steine an einen belie­bigen Ort der Welt versetzen würde, nahe beiein­ander außer­halb des Kraft­bereichs eines dritten verwandten Körpers, dann würden sich jene Steine ähn­lich wie zwei magne­tische Körper an einem zwischen­liegenden Ort vereinigen, wobei sich der eine dem andern um eine Strecke nähert, die der Masse des andern propor­tional ist.

• Der Bereich der Anziehungs­kraft des Mondes erstreckt sich bis zur Erde.

Ebenfalls Anfang des 17. Jahrhunderts beschrieb Galileo Galilei (1564-1642) den freien Fall eines Körpers als gleich­mäßig beschleunigte Bewegung. Diese Bewegung sei unab­hängig von seiner Masse oder sonstigen Beschaffen­heit.

René Descartes erklärte die Schwer­kraft als Folge seiner „Wirbel­theorie”. 1644 veröffent­lichte er die Principia Philosophiae, die zunächst großen Einfluss hatten. Aller­dings übte Isaac Newton Kritik an dessen Theorie, weil die Kometen nicht mit Descartes Modell erklärt werden könnten. Dass Kometen die Sphären bzw. die Bahnen der Planeten durch­dringen bzw. kreuzen, war seit Tycho Brahe und dem Kometen von 1577 die vorherr­schende Meinung.^[4]

Die „Wirbel­theorie” wurde von Christiaan Huygens zwischen 1669 und 1690 weiter­entwickelt, aber sie trat im Laufe der Zeit immer mehr in den Hinter­grund.

Der englische Gelehrte Robert Hooke erklärte um 1670 die Wirkung der Gravita­tion mithilfe von „Gravitations­trichtern”. Er vertrat die Auffassung, dass die Gravita­tion eine Eigen­schaft aller masse­behafteten Körper sei. Nach seiner Über­legung sei die Gravita­tion umso größer, je näher sich zwei Körper zuein­ander befänden. Die Theorie, dass die Schwer­kraft umgekehrt propor­tional zum Quadrat des Abstands vom Masse­zentrum ist, taucht erstmals 1680 in einem Brief Hookes an seinen Landsmann Newton auf.

Isaac Newton beschrieb in seiner Principia als erster die Gravita­tion mithilfe einer mathe­matischen Formel. Dieses von ihm formu­lierte Gravitations­gesetz ist eine der Grund­gleichungen der klassischen Mechanik. Es war die erste physika­lische Theorie, die man auch in der Astro­nomie anwandte. Newton bezeichnete die Gravita­tion als eine Kraft, die zwischen zwei Körpern wirkt und diese zu ihrem gemein­samen Schwer­punkt hin beschleu­nigt. Wobei die Stärke der Gravita­tion propor­tional zum Quadrat des Abstandes der Körper abnimmt.

Die Newton'sche Theorie, wurde um 1800 von Pierre-Simon Laplace vollendet. Sie lieferte bisher ein grund­legendes Verständnis der Dynamik des Sonnen­systems mit der Möglich­keit präziser Vorher­sagen der Bewegung von Planeten, Monden und Kometen. Des Weiteren scheint sie die Kepler'schen Gesetze der Planeten­bewegung für einzelne Planeten zu bestätigen.

Die danach berechneten Werte stimmten lange Zeit mit den entspre­chenden astro­nomischen und irdischen Beobach­tungen und Experi­menten voll­kommen über­ein. Dennoch gab es Mitte des 19. Jahrhunderts eine erste mit dieser Theorie nicht erklär­bare Diskrepanz. Denn die Perihel­drehung der Bahn des Merkur wider­spricht der Newton'schen Theorie. Doch dazu später mehr.

Abb.: Das Newtonsche Gravitationsgesetz

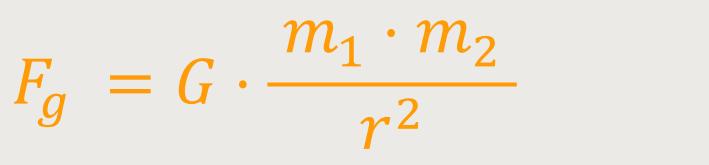
Zur Erklärung der Gravita­tion im Sinne eines Prozess­geschehens wurden im weiteren Verlauf eine Reihe mecha­nischer bzw. kinetischer Erklärungen vorge­schlagen. Eine der bekann­testen ist die von Fatio und Le Sage entwickelte Theorie der Le-Sage-Gravitation. Dieser Theorie zufolge beruht die Gravitations­anziehung zweier Körper auf der Abschirmung des aus Richtung des jeweils anderen wirkenden Drucks.

Im Zusammen­hang hiermit stehen die Theorien eines Äthers als Vermittler von Wechsel­wirkungen, anstelle einer Fern­wirkung. Eine der letzten dieser Theorien war die um 1900 entstandene Lorentz'sche Äthertheorie, die schließlich von dem neuartigen Ansatz der Einstein'schen Relativitätstheorie verdrängt wurde.

In der 1916 von Albert Einstein aufge­stellten Allgemeinen Relativitätstheorie (ART) wird die Gravita­tion auf eine geome­trische Eigen­schaft der Raum­zeit zurück­geführt. Nach seiner Auffassung wird die Raum­zeit durch die Anwesen­heit von Masse und jeglicher Form von Energie gekrümmt. Durch diese Sicht­weise ist es möglich, die Gravitation grundsätz­lich anders zu inter­pretieren als die anderen Kräfte. Die Gravitation lässt sich dann als Trägheits­kraft ansehen.

Nach dem Äquivalenz­prinzip kann die Wirkung der Gravita­tion nicht von der Auswirkung einer Beschleunigung des Bezugs­systems unter­schieden werden. Denn in einem frei fallenden Bezugs­system heben sich die Wirkungen von Gravita­tion und Beschleu­nigung exakt auf. Man sagt, die Gravita­tion sei durch den Über­gang zu den neuen Koordinaten „wegtrans­formiert”. Aller­dings gilt dies jeweils nur für einen Ort. Denn jedes reale Gravitations­feld bewirkt für benach­barte Orte abweichende Beschleu­nigungen.

In der Allge­meinen Relativitäts­theorie wird zu jedem Punkt im Raum das entspre­chende Lokale Inertial­system ermittelt. In einem solchen System gibt es keine Gravita­tion und es hat dort jeweils die Spezielle Relativitäts­theorie Gültig­keit. Die Wirkung der Gravita­tion tritt erst wieder bei der Rück­trans­formation in das Bezugs­system des Beobachters zutage.

Analog dazu bewegen sich in der Allge­meinen Relativitäts­theorie Körper ohne gravitative Kräfte auf Geodäten in einem „gekrümmten” Raum mit Riemannscher Geometrie. Dies entspricht auch Galileis Aussage, dass kräfte­freie Bewegungen gerad­linig und gleich­förmig verlaufen.

Um die an einem Punkt herrschende Krümmung der Raum­zeit bestimmen zu können, bedient man sich der Einstein'schen Feld­gleichungen. Sie wurden so formuliert, dass im Grenz­fall bei schwach wirkender Gravita­tion die nach ihnen berech­neten Ergeb­nisse mit denen der Newton'schen Gleichung überein­stimmen. Die Allge­meine Relativitäts­theorie behandelt die Gravita­tion also als „Trägheits­kraft”. Damit wird sie mit der Zentrifugal­kraft, der Coriolis­kraft oder der Beschleu­nigungs- bzw. Verzögerungs­kraft auf eine Stufe gestellt.

Inner­halb eines Sonnen­systems, wo es sich um schwache Felder bzw. eine geringe Krümmung der Raum­zeit handelt, ergeben sich nur geringe Abweichungen von den Vorher­sagen des Newton'schen Gravitations­gesetzes. Das erste erfolg­reiche Anwendungs­beispiel der Allge­meinen Relativitäts­theorie war die Erklärung der Diskrepanz um den Planeten Merkur. Die ART konnte die kleinen Abweichungen zwischen der beobachteten Perihel­drehung der Bahn des Merkur und dem Wert, der nach der Newton'schen Theorie aufgrund der Bahnstörungen durch die anderen Planeten vorhergesagt wurde, erklären.

Bei starker Krümmung, wie sie durch starke Konzen­tration großer Massen auf kleinem Raum hervor­gerufen wird, werden völlig neue Phänomene wie beispiels­weise Schwarze Löcher vorher­gesagt.

Bei der Newton'schen Mechanik wird allein die Masse als Ursache für die Gravita­tion zugrunde gelegt. In der Allge­meinen Relativitäts­theorie ist die Gravita­tion dagegen Ausdruck der Krümmung der Raum­zeit. Bei der ART spielt nicht nur die Anwesen­heit von Materie eine Rolle, sondern auch jegliche Form von Energie. Man spricht in diesem Zusammen­hang auch von der Gravitations­energie und von Massen- und Energie­strömen. Ein unschlag­bares Argument ist, dass alle Vorher­sagen der ART, die sich beobachten lassen, auch durch entspre­chende Messungen bestätigt wurden.

In der Newton'schen Gravitation geht man noch von einer instan­tanen Ausbreitung der Gravitations­wirkung aus, das heißt, dass die Wirkung auch über große Entfer­nungen sofort erfolgt. Inner­halb der Einstein'schen Sicht­weise gilt jedoch, dass sich keine Wirkung, also auch nicht die Gravitations­wirkung, schneller als mit Licht­geschwin­digkeit ausbreitet.

Gibt es noch eine andere Sicht­weise der Gravita­tion? Ja, es gibt eine Möglich­keit, die 4-dimensionale Krümmung der Raum-Zeit mit der bereits 1644 in Betracht gezogenen „Wirbeltheorie” zu verbinden. Allerdings laufen die Mechanismen etwas anders ab, als es René Descartes seiner­zeit in Erwägung gezogen hat. Wir werden diese Theorie im letzten Bereich neu aufbereiten.

Ein Theoretischer Physiker ist in der Natur auf Gesetz­mäßig­keiten gestoßen, die neue Einsichten in die detallierten Abläufe gibt, die letztlich zu einem Konsens führen. Insofern wird eine frühere Theorie, die als begraben schien, wieder zutage gefördert und ihr auf wundersame Weise neues Leben einge­haucht. Wir hoffen, dass der Leser genauso begeistert ist, wie es bei uns der Fall ist.

Quellen

[1] Edward Grant: The Nature of Natural Philosophy in the Late Middle Ages. Washington 2010, S. 63; Planets, Stars, and Orbs: The Medieval Cosmos, 1200-1687. 1994/96, S. 165; A Source Book in Medieval Science, Band 1. Zusammengestellt von Edward Grant, 1974, S. 551; Paul S. Agutter, Denys N. Wheatley: Thinking about Life: The history and philosophy of biology and other sciences. 2008, S. 59
[2] zitiert nach: Nicolaus Coppernicus aus Thorn über die Kreisbewegungen der Weltkörper. (Deutsche übersetzung von C. L. Menzzer, 1879.), S. 23
[3] Astronomia nova. Neue ursächlich begründete Astronomie (übersetzung von Max Caspar, 1929 und Fritz Krafft, Wiesbaden 2005.), S. 28-29
[4] Harry Nussbaumer: Revolution am Himmel: wie die kopernikanische Wende die Astronomie veränderte. Zürich 2011, S. 237; Eberhard Knobloch: Das Weltbild in den Wissenschaften - Geschichte einer Konzeption. in: Christoph Markschies, Johannes Zachhuber (Hrsg.): Die Welt als Bild: Interdisziplinäre Beiträge zur Visualität von Weltbildern. Berlin 2008, S. 227-246, S. 242

⇦ Kapitel Kapitel ⇨