Die meisten von uns haben den Begriff „Spirale” schon einmal gehört. Aller­dings verbindet jeder etwas anderes mit diesem doch nicht alltäg­lichen Begriff. Würde man uns dazu befragen, denken viele vielleicht zuerst an die Familien­planung. Einem anderen kommt aus beruf­licher Sicht ein „Spiral­bohrer” oder eine „Spiral­feder” in den Sinn. Hobby­astronomen denken womög­lich eher an eine „Spiral­galaxie”. Wer gerne in der Natur unter­wegs ist, stößt oftmals unbewusst bei Schnecken­häusern, Sonnen­blumen oder Tannen­zapfen auf „Spiralkurven”.

Aus technischer Sicht ist eine Spirale, auch Schnecken­linie genannt, eine Kurve, die um einen Punkt oder eine Achse verläuft und sich je nach Perspek­tive des Betrach­ters von diesem Zentrum entfernt oder sich ihm annähert. Spiralen werden oft auch zur Konstruktion von krümmungs­stetigen Übergangs­kurven verwendet. Die Spirale wird manchmal mit der Schraube verwechselt.

Abb. 1: Die Kalkschale der Ammoniten gleicht einer logarithmischen Spirale (CC BY-SA 3.0)

Während die proto­typische Spirale ein Gebilde in der Ebene ist, wie zum Beispiel die Rille einer Schall­platte, ist sowohl die Schraube als auch der Spiral­bohrer ein räum­liches Gebilde entlang des Hofes eines Zylinders. Die Schrauben­linie oder zylin­drische Spirale bzw. Wendel wird auch als Helix bezeichnet. Bei ihr handelt es sich um eine Kurve, die sich mit konstanter Steigung um den Mantel eines Zylinders windet. Bei unserer Betrachtung geht es aber weniger um Schrauben, wenn­gleich sie sich sehr gut eignen, Bauteile mit einander zu verbinden.

Aus mathe­matischer Sicht, hat sich der eine oder andere viel­leicht während der Schul­zeit mit mehr oder weniger Begei­sterung schon einmal dem Kurven­verlauf einer Spirale gewidmet. Man ist viel­leicht über­rascht zu hören, wie viele verschiedene Spiral­typen es gibt. Die geläu­figsten sind zum Beispiel die Archime­dische Spirale, die Galile­ische Spirale und die Logarith­mische Spirale. Darüber hinaus gibt es die Hyper­bolische Spirale, die Fermatsche Spirale und die Lituus-Spirale. Andere Varianten sind die Spirale 3. Grades in r oder die Spirale 3. Grades in φ.

Die Mathematik definiert alle diese verschie­denen Spiral­typen, die sich aller­dings in ihren Eigen­schaften und ihrem Aussehen mitunter stark vonein­ander unter­scheiden. Spirale ist tatsäch­lich nicht gleich Spirale.

Wenn wir uns in den nach­folgenden Kapiteln einge­hender mit den zuvor genannten Spiralen beschäf­tigen, geht es um die Frage, warum die Natur bestimmte Spiralen zu bevorzugen scheint. Welche dieser Spiralen eignet sich womög­lich, um den Wachstums­mechanismus in der Natur wieder­zugeben? Gerade Schnecken­häuser und Sonnen­blumen weisen ein­deutig festge­legte Spiral­muster auf. Zudem treten bei Wachstums­spiralen sowohl links- als auch rechts­läufige Spiralen in Erscheinung.

Wie wir bereits in den vor­herigen Kapiteln gesehen haben, schließt jede neue Anlage (Blatt oder Samen) einen ähn­lichen Divergenz­winkel ein. Jede Pflanze hat zudem einen für sich charakte­ristischen Divergenz­winkel. Dieser Winkel orientiert sich an dem bereits betrachteten Goldenen Winkel. Während Pflanzen ein dynamisches Wachstum wider­spiegeln, bilden Schnecken­häuser eher statische Objekte. Sie „wachsen” zwar auch mit dem Alter der Schnecken, aller­dings wird nur an der Öffnung des Gehäuses eine weitere Kalk­schicht an die bereits vorhandene Kalk­schicht gefügt, und zwar nach einem logarith­mischen Prinzip. Daher gleichen sich alle Schnecken­häuser auf verblüffende Weise.

Man spricht in diesem Zusammen­hang auch gerne von rotations­symme­trischen Strukturen, wenn das betrachtete Objekt einen zentralen Punkt besitzt, und die Kontur auf sich selbst abgebildet werden kann. Bei den meisten Betrachtungen handelt es sich um in die Ebene projizierte 2-dimensionale Spiralen. Doch fairer­weise müsste man auch die dritte Dimension mit einfließen lassen.

Sämtliche Gebilde in der Natur haben eine endliche Anzahl von Windungen, die um einen Pol verlaufen. Der Abstand zwischen den Spiral­punkten nimmt streng monoton zu oder ab. In den meisten Fällen ist der Pol ein asympto­tischer Punkt, den die immer enger werdenden Windungen nie erreichen.

Man kann Spiralen mathe­matisch am besten als Koordinaten­gleichungen im ebenen Polar­koordinaten­system beschreiben. Wie wir anschließend noch sehen werden, wird jeder Spiraltyp durch eine spezi­fische Gleichung beschrieben, die jeweils den Radius in Abhängig­keit des Winkels definiert.

Es gibt eine dynamische Mathe­matik­software, die sich „GeoGebra” nennt, mit deren Hilfe sich Geometrie, Algebra und Analysis ver­binden lassen. Jeder Punkt auf der Spirale lässt sich so durch die entsprechende Gleichung der jeweiligen Spirale beschreiben. Um alle Punkte der ersten Windung der betreffenden Spirale zu erhal­ten, muss der Winkel φ alle Werte von Null bis 2π durch­laufen. Mit GeoGebra ist es möglich, einen Punkt A auf der x-Achse beliebig weit nach rechts laufen zu lassen, so dass seine x-Koordinate wie gewünscht alle Werte von Null bis 2π durchläuft.

Durch Drehen oder Verschieben des Pols lassen sich die mathe­matischen Spiralen mög­lichst gut an die natür­lichen Spiralen anpassen. In GeoGebra können mithilfe von Schiebe­reglern weitere Parameter hinzuge­fügt werden, wodurch gewisse Feinab­stimmungen möglich sind. Das ganze lässt sich natürlich auch für versierte Anwender mit einer Excel-Tabelle in Kombination mit einer Grafik realisieren.

Wir müssen jedoch grund­sätzlich zwischen zwei Prinzipien unter­scheiden. Schnecken­gehäuse weisen nur eine Spirale auf, wogegen die Frucht­stände aller Pflanzen zwei gegen­läufige Spiralen besitzen. Jede Pflanze weist verschieden steile rechts- und links-drehende Spiralen­scharen auf, sprich Spiralen, die denselben Drehsinn haben und die gleiche Steigung besitzen.

Bei den Gehäusen verschiebt man zunächst den mathe­matischen Pol solange, bis er möglichst deckungs­gleich mit dem der natür­lichen Spirale über­einstimmt. Anschlie­ßend wird der Parameter a solange gestreckt oder gestaucht, bis eine Ähnlichkeit der Spirale vorhanden ist. Dennoch nimmt dieser Parameter eher eine unter­geordnete Rolle ein. Viel wichtiger ist, wie sich zum Beispiel bei der Loga­rith­mischen Spirale, der Parameter k verhält, der den konstanten Tangenten­winkel der Spirale festlegt. Dieser Parameter bestimmt die Steigung und kann durch „Fein­tuning” angepasst werden.

Wer sich die Mühe macht, das selbst einmal auszu­probieren, wird fest­stellen, dass die Überein­stimmung der mathe­matischen Spiral­typen mit der natür­lichen Spirale sehr stark von den Radien­differenzen abhängt. Mit anderen Worten, die Spirale läuft zwar mit der entspre­chenden Gleichung um den Pol, aber es gibt dennoch geringe Abwei­chungen pro Windung.

Dies resultiert sowohl bei den Schnecken­häusern als auch bei den Frucht­ständen aus der Nährstoff­zufuhr, die das Wachstum maßgeb­lich beein­flusst. Ein klassisches Beispiel sind die Jahres­ringe eines Baums, die nicht alle gleich dick ausfallen. Der Baum wächst zwar grund­sätzlich nach einem genetisch festge­legten Muster, aber pro Lebens­abschnitt doch unter­schiedlich schnell. Diese Diskrepanz lässt sich auch auf die Spiral­kurven übertragen.

Man kann sich noch so viel Mühe geben, die Radien­differenzen statistisch zu bewerten. Selbst die Summe aller Radien­differenzen zu bilden hilft nicht wirklich weiter. In diesem Fall würden jene Spiral­typen benach­teiligt, welche bei den inneren Windungen eines Gehäuses gut passen, bei den äußeren jedoch schlechter. Das hat damit zu tun, dass die Radien der äußeren Windungen grund­sätzlich länger sind, und entsprechend zu größeren Radien­differenzen führen.

Einige Spiral­typen scheiden bereits aufgrund ihrer Eigen­schaften aus, da sie sich nicht auf die natür­lichen Spiralen abbilden lassen. Dazu gehören die Lituus Spirale und die Hyperbolische Spirale, die z.B. deren Pol nie erreichen.

Die Windungs­abstände der fermatschen Spirale und der Spirale 3. Grades in r werden mit zuneh­mendem Polar­winkel φ sogar immer enger. Des Weiteren verläuft die Spirale bei Annähe­rung an den Pol flacher. Somit scheidet auch sie aus, weil der Windungs­abstand bei Schnecken­häusern mit zunehmender Entfernung vom Pol vielmehr zunimmt.

Die Archimedische Spirale stimmt zwar oft bei den ersten zwei Windungen mit der natür­lichen Spirale überein. Sie hat auch im Vergleich mit den anderen Spiral­typen die wenigsten Radien­diffe­renzen. Doch ab der zweiten Windung nimmt der Windungs­abstand bei den natür­lichen Spiralen schneller zu, zumal die Archimedische Spirale grund­sätzlich einen konstanten Windungs­abstand aufweist.

Alles in allem bleiben nur drei Spiral­typen übrig, die einer näheren Betrachtung würdig sind: Die Galileische Spirale, die Logarithmische Spirale und die Spirale 3. Grades in φ. Statistisch gesehen gibt es bei allen drei Spiral­typen die gleichen Überein­stimmungen zu der natür­lichen Spiralen bei Schnecken­häusern.

Dennoch sticht die Logarith­mische Spirale heraus, weil sie am besten auf einzelne Windungen der natür­lichen Spirale angepasst werden kann. Die Anpassungen bewegen sich ähnlich wie bei den Frucht­körben nur im 1/100 bis 1/1000 Bereich.

Die nach­folgende Grafik zeigt, wie die Logarith­mische Spirale beim Schnecken­gehäuse verläuft, wenn die Steigung der Kurve konstant bleibt. Wie bereits erwähnt resultieren die Abwei­chungen aus der schwankenden Nährstoffzufuhr.

Abb. 2: Logarithmische Spirale mit konstanter Steigung

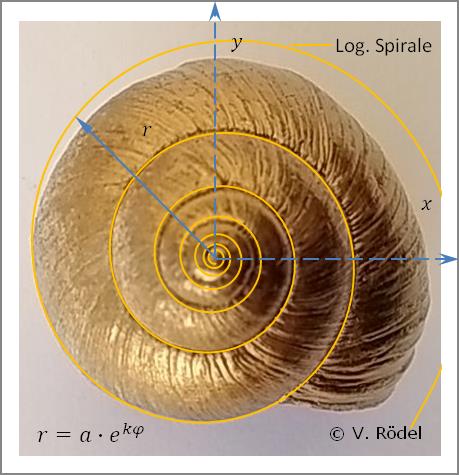
Berücksichtigt man aller­dings die Nähr­stoff­zufuhr beim Wachstum des Schnecken­gehäuses, zeigt sich eine erstaun­liche Deckungs­gleich­heit. In der nächsten Grafik wurde die Steigung der Windungen im gesamten Verlauf pro 90°-Winkel um weniger als 1/1000 ange­passt.

Das sind nur marginale Anpassungen, die aber letztlich einen nahezu perfekten Spiralverlauf abbilden.

Abb. 3: Logarithmische Spirale mit leicht angepasster Steigung im 1/1000 Bereich

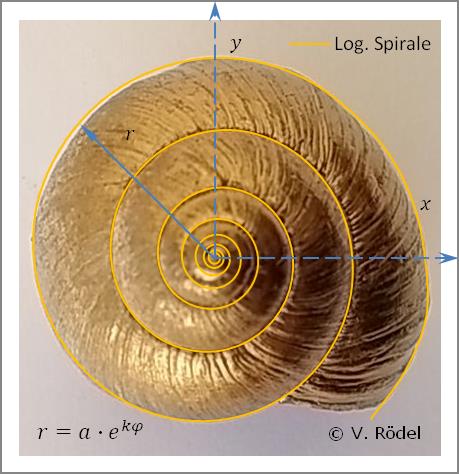
Diese geringen Abweichungen lassen sich bei allen Schnecken­häusern beobachten. Oberfläch­lich betrachtet scheint es zunächst so, als wenn verschiedene Spiral­typen zum Tragen kommen, um alle Windungen abbilden zu können. Tatsäch­lich aber bildet nur die Logarith­mische Spirale die einzig wahr­haftige Grundlage.

Auch bei den Ammoniten kommen eben­falls nur die drei zuvor favorisierten Spiral­typen zur Auswahl. Doch letzt­lich nimmt auch hier nur der Radius der Logarith­mischen Spirale exponentiell zu, eine Grund­voraus­setzung für die natür­lichen Spiralen. Noch präziser fällt das Ergebnis bei der Schale des Nautilus aus. Die Überein­stimmung mit der Logarith­mischen Spirale ist nahezu perfekt.

Abb. 4: Nautilus Muschel (CC BY-SA 4.0)

Bei den Frucht­ständen jedoch scheint die Logarith­mische Spirale auf den ersten Blick nicht mit den natür­lichen Spiralen überein­zustimmen. Hier passt augen­scheinlich die Steigung der Spirale nicht mit den Frucht­ständen überein. Bei genauer Betrachtung stellt sich sogar heraus, dass die links- und rechtsläufigen Spiralen nicht die gleiche Steigung aufweisen.

Doch genau diese Steigung ist letztlich der Schlüssel zum Erfolg. Denn verwendet man unein­geschränkt die Logarith­mische Spirale als Grund­lage, jedoch mit einer wesen­tlich flacheren Steigung, erhält man das gewünschte Ergebnis. Und wie gesagt, es muss auch hier die Steigung je nach Nähr­stoff­zufuhr pro Windungs­abschnitt im 1/100 Bereich angepasst werden.

Abb. 5: Spiralmuster bei der Sonnenblume (lizenzfrei)

Außerdem dürfen wir eines nicht außer Acht lassen: Wir betrachten ein in der Natur 3-dimensionales Erscheinungs­bild auf einem Foto nur 2-dimensional. Durch die Fotografie wird der 3-dimensionale Spiral­verlauf auf eine Ebene projiziert. Das Verhältnis zwischen den Windungs­abständen bleibt dabei zwar erhalten. Doch nur ein kleiner Winkel­versatz beim Foto­grafieren, entweder weil die Achse des Objekts nicht lotrecht zur Ebene oder die Kamera nicht lotrecht zum Objekt ausge­richtet ist, verfälscht das Ergebnis.

Je nachdem von welchen Über­legungen man sich leiten lässt, und wie statisch man an die Betrachtungs­weise heran­geht, desto einge­schränkter wird das Ergebnis und dessen Schluss­folgerungen ausfallen.

Egal, um welches Objekt es sich handelt, grund­sätzlich kommen bei natür­lichen Spiralen nur drei in die engere Wahl: Die Galileische Spirale, die Logarithmische Spirale und die Spirale 3. Grades in φ. Des Weiteren muss der gesuchte Spiraltyp einen asympto­tischen Punkt aufweisen, denn nichts in der Natur wächst von Null aus. Die Basis bildet bevorzugt eine ring­förmige Molekular­struktur, auch wenn sie mikros­kopisch klein ist.

Man kann natür­lich auch jede Windung für sich betrachten. So besteht viel­leicht bei der ersten Windung eine Ähnlich­keit mit der Galileischen Spirale, bei der zweiten Windung eine Ähnlichkeit mit der Logarithmischen Spirale und bei weiteren Windungen womöglich eine Ähnlichkeit mit der Spirale 3. Grades in φ. Das liegt einfach daran, dass die mathe­matischen Gleichungen dieser drei Typen eine gewisse Ähnlichkeit aufweisen.

Tatsächlich aber ist und bleibt nur die „Logarithmische Spirale” die einzig wahre Umsetzung, wie wir in den späteren Kapiteln noch sehen werden.

Im Nach­folgenden werden wir einige der wichtigsten „Ebenen Spiralen” betrachten und diese im Anschluss auf eine Räumliche Geometrie übertragen.

⇦ Kapitel Kapitel ⇨