Im Nach­folgenden werden wir einige der wichtigsten Räum­lichen Spiral­kurven abbilden. Wir haben sie bereits schon als Ebene Spiralen kennen­gelernt.

Auch die „Räum­lichen Spiral­kurven” lassen sich mathe­matisch am besten als Koordinaten­gleichungen mittels ebenem Polar­koordinaten­systems beschreiben. Der Radius r wird dabei als Funktion r(φ) von φ dargestellt. Der Winkel φ läuft im Allge­meinen gegen unend­lich, anstatt nur einen Umlauf bis 2π. Auch negative Winkel sind möglich.

Unter einer konischen Spirale versteht man eine Kurve, die auf einem senk­rechten Kreis­kegel abgebildet wird. Die Projektion bzw. deren Grund­riss ist eine ebene Spirale. Handelt es sich bei dem Grund­riss um eine Logarith­mische Spirale, so spricht man auch von einer „Concho-Spirale”, abgeleitet von Conch (Wasserschnecke).

Wie die Logarith­mische Spirale selbst, so spielt auch die mit ihr konstruierte Concho-Spirale in der Biologie bei der Gestaltung von Schnecken­häusern eine wesent­liche Rolle.

Wie wir uns erinnern, ist bei Ebenen Spiralen die Polardarstellung definiert als:

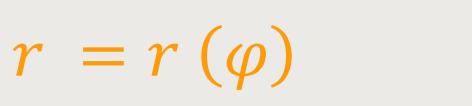
In x-y-Koordinaten werden dadurch Punkte mit folgender Parameter­darstellung beschrieben:

Um eine ebene Spirale „räumlich” abzubilden, wird eine dritte Koordinate hinzugefügt:

Die dadurch auf einem senk­rechten Kreis­kegel entstehende räum­liche Kurve beschreibt die Gleichung:

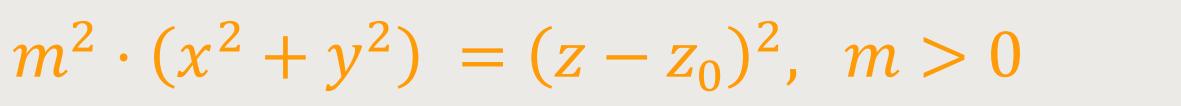
In x-y-z-Koordinaten werden dadurch Punkte mit folgender Parameter­darstellung beschrieben:

Der Parameter m ist die Steigung der Kegel­geraden gegen­über der x-y-Ebene.

Zur Konstruktion einer konischen Kurve dient der Grund­riss der entspre­chenden ebenen Spirale. Insofern kann man die konische Spirale auch als ortho­gonale Projektion der Grundriss-Spirale auf den Kegel­mantel ansehen.

Eine konische Spirale auf Basis der „Archimedischen Spirale” lässt sich beschreiben als:

Abb. 1: Archimedische Spirale (rechts­drehend; in positiver Richtung zunehmend)

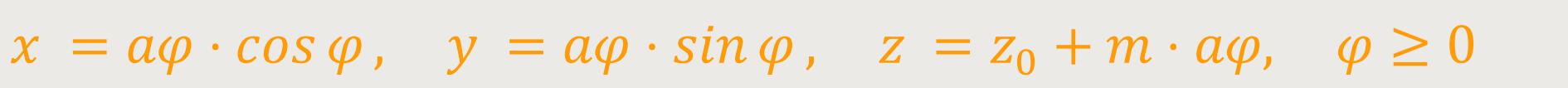
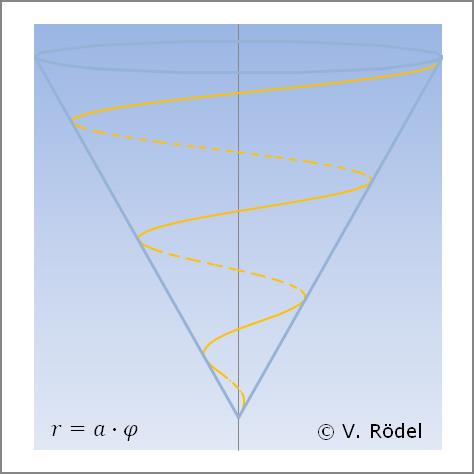
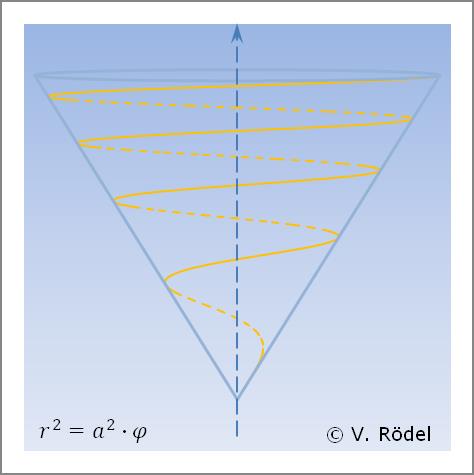
Eine konische Spirale auf Basis der „Fermatschen Spirale” lässt sich beschreiben als:

Abb. 2: Fermatsche Spirale (rechts­drehend; in positiver Richtung zunehmend)

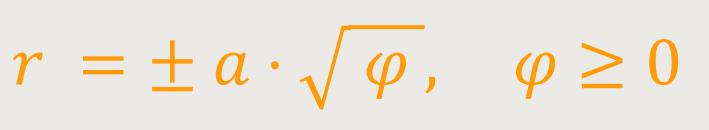
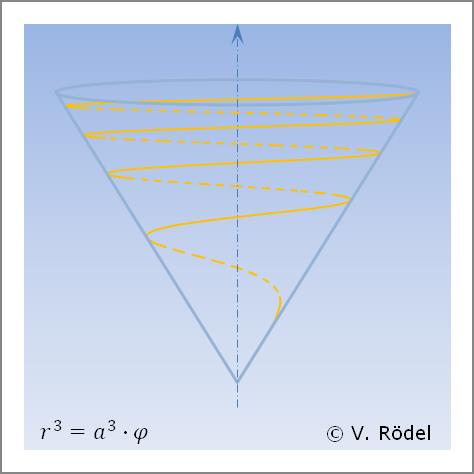
Eine konische Spirale auf Basis des „3. Grades in r” lässt sich beschreiben als:

Abb. 3: Spirale 3. Grades in „r” (rechts­drehend; in positiver Richtung zunehmend)

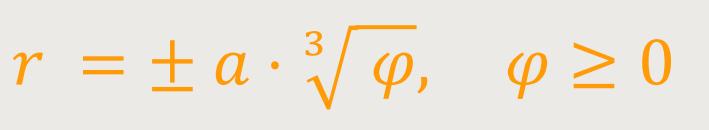
Eine konische Spirale auf Basis der „Galileischen Spirale” lässt sich beschreiben als:

Abb. 4: Galileische Spirale (rechts­drehend; in positiver Richtung zunehmend)

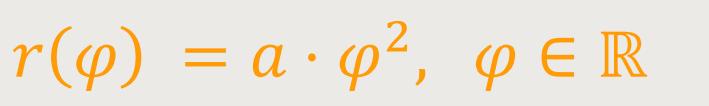
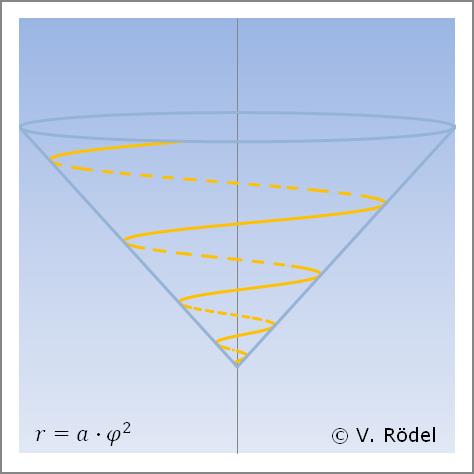
Die Galileische Spirale gleicht der nach­folgenden Spirale auffallend. Sie verläuft gegen­über der Logarith­mischen Spirale aller­dings etwas flacher.

Eine konische Spirale auf Basis der „Logarith­mischen Spirale” lässt sich beschreiben als:

Abb. 5: Logarithmische Spirale (rechts­drehend; in positiver Richtung zunehmend)

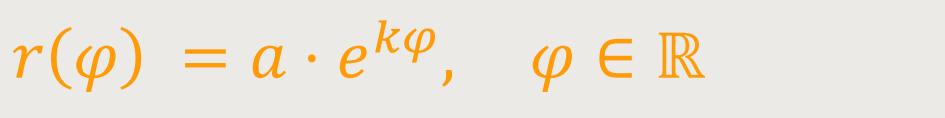
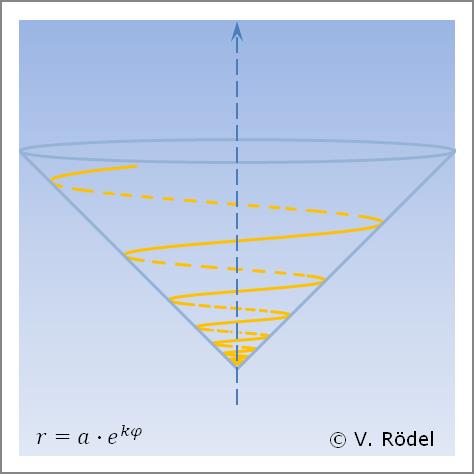
Im Nach­folgenden werden die Eigen­schaften konischer Spiralen mit Grund­rissen nach folgender Form beschrieben:

Unter der Steigung einer konischen Spirale versteht man die Steigung der Spirale (Tangente) gegen­über der Horizontalen (x-y-Ebene). Der zugehörige Steigungs­winkel ist definiert als:

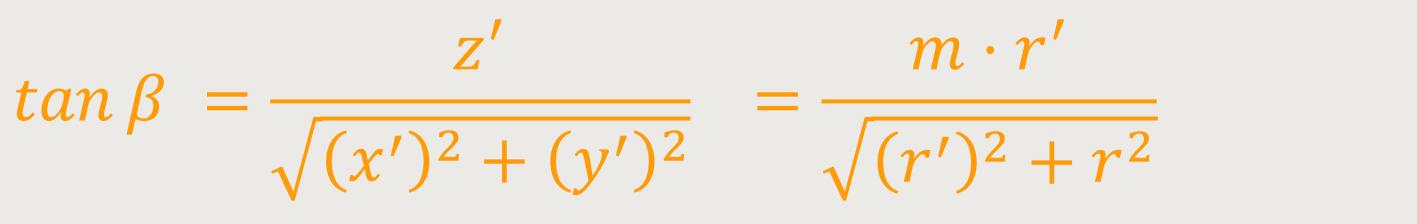
Für eine Spirale mit r = a · φⁿ ergibt sich entsprechend:

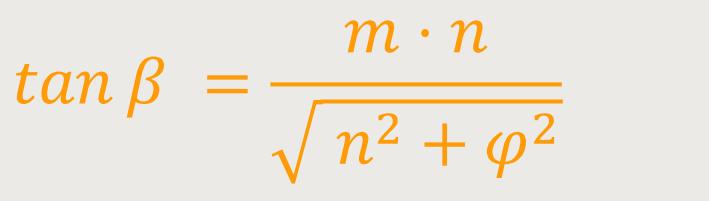
Wird beispiels­weise bei einer Archime­dischen Spirale für n = 1 gewählt, erhält man die Steigung:

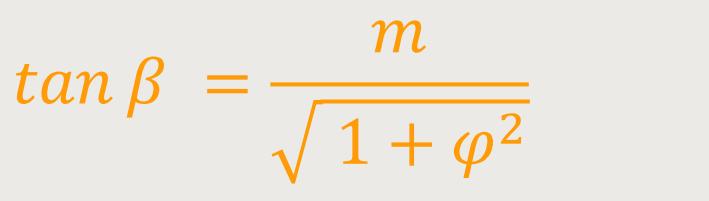
Für eine logarith­mische Spirale mit r = a · e^kφ erhält man die Steigung:

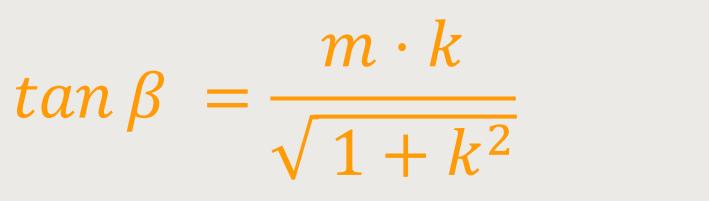
Da die Steigung in diesem Fall konstant ist, heißt die Concho-Spirale (s.o.) deswegen auch gleich­schenklige konische Spirale.

Die Länge eines Kurven­bogens einer konischen Spirale ist definiert als:

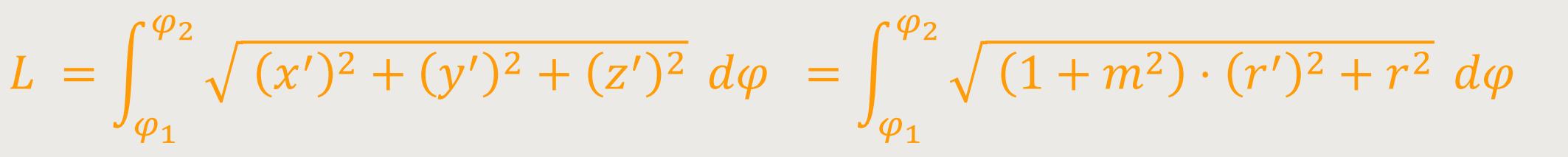
Dieses Integral ist für eine Archime­dische Spirale mittels einer Integrations­tabelle lösbar. Man erhält entsprechend:

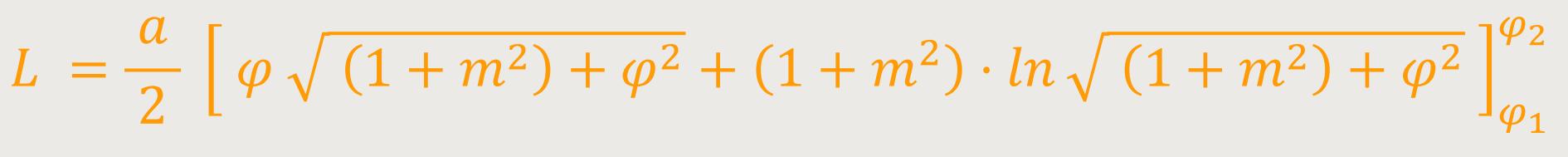
Für eine Logarith­mische Spirale lässt sich obiges Integral leichter lösen:

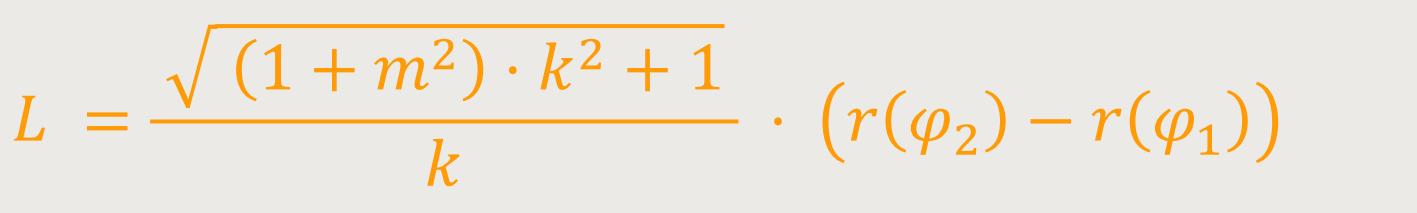
⇦ Kapitel Kapitel ⇨