In diesem Teil werden wir die Ebenen Spiralen noch um einige Varianten vervollständigen.

Eine Hyper­bolische Spirale ist eine ebene Kurve, die sich in der r-φ-Ebene in Polar­darstellung durch die Gleichung einer Hyperbel beschreiben lässt. Sie entsteht unter anderem bei der Zentral­projektion einer Schrauben­linie auf eine zur Schrauben­achse senk­rechte Ebene. Da sie sich auch als Inversion (Kreis­spiegelung) einer Archime­dischen Spirale auffassen lässt, bezeichnet man die Kurve auch als „reziproke Spirale”.

Die Polardarstellung der Hyper­bolischen Spirale ist definiert als:

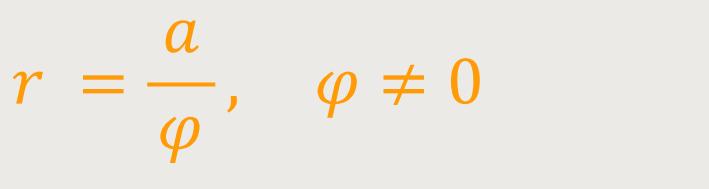
Sie lässt sich in kartesischen Koordinaten ( x = r ·cos φ, y = r · sin φ ) durch die Parameter­darstellung beschreiben:

Abb. 1: Hyperbolische Spirale (rechtsdrehend)

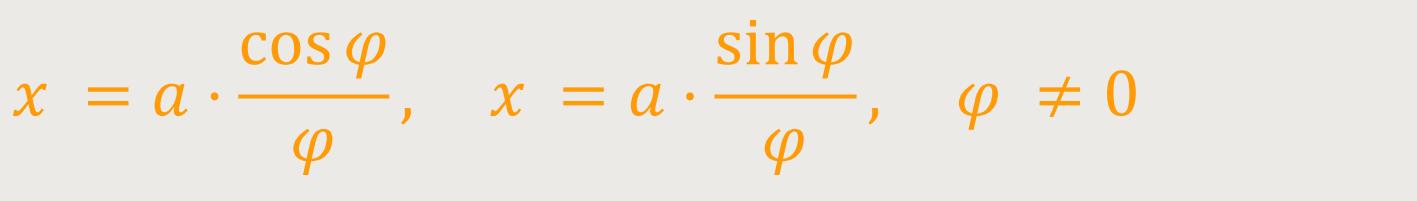
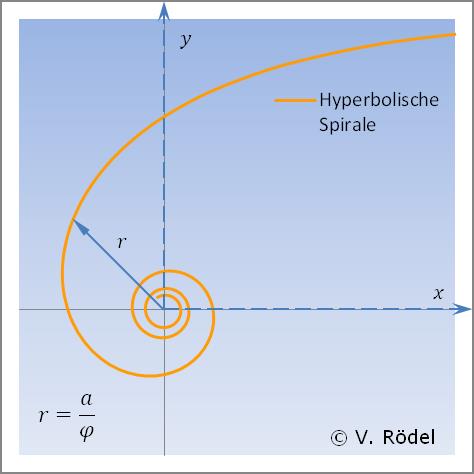
Die Hyperbel in der r-φ-Ebene besitzt die Koordinaten­achsen als Asymptoten. Die Hyper­bolische Spirale in der x-y-Ebene nähert sich für φ → ± ∞ dem Null­punkt an. Für φ → ± ∞ ergibt sich eine Asymptote.

Aus obiger Parameter­darstellung und

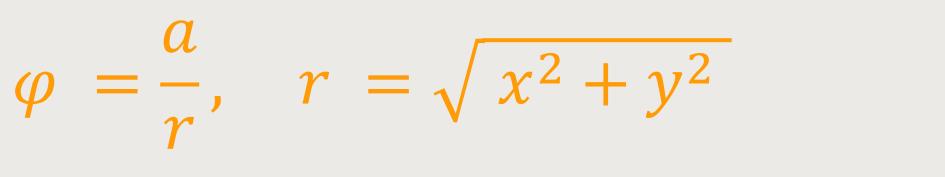
ergibt sich eine Darstellung mit der Gleichung:

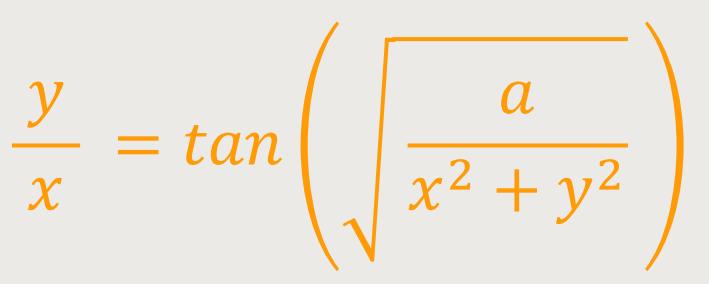
Die Krümmung k einer Kurve in Polar­darstellung ist definiert als:

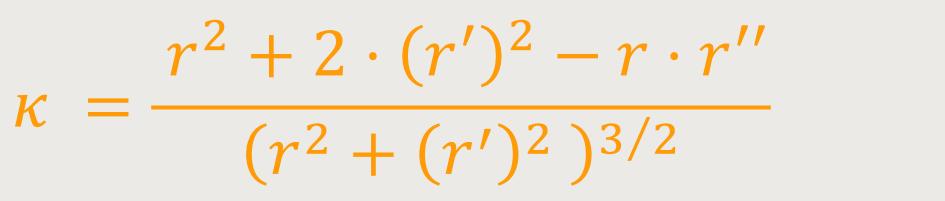
Für die Krümmung einer Kurve in Polar­darstellung r = r(φ) und den Ableitungen der Hyper­bolischen Spirale

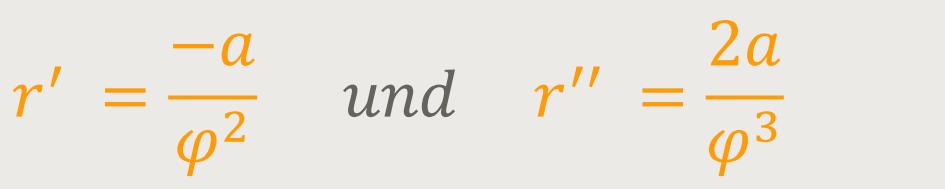
ergibt sich die Krümmung:

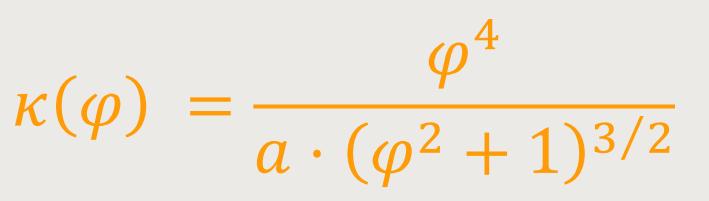
Die Spiegelung am Einheits­kreis (Inversion) lässt sich in Polar­koordinaten beschreiben durch:

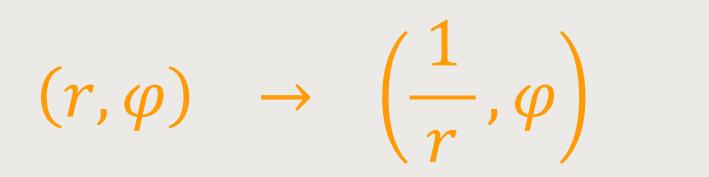
Insofern ergibt sich als grafische Darstellung der „Archime­dischen Spirale” bei der Spiegelung am Einheits­kreis die „Hyperbo­lische Spirale”.

Für φ = a schneiden sich beide Kurven in einem Fixpunkt auf dem Einheits­kreis.

Der Krümmungs­kreis der Archime­dischen Spirale hat im Null­punkt den Radius ρ_₀ = 1/2a und den Mittel­punkt (0, ρ_₀ ).

Dieser Kreis geht bei der Kreis­spiegelung in die Gerade y = a über.

Abb. 2: Inversion der archimedischen Spirale

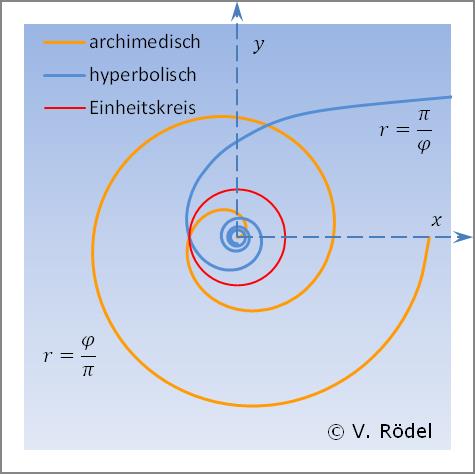
Das Bild zeigt a = π. Der Kurven­bogen der Archime­dischen Spirale (orange), welcher im Einheits­kreis (rot) liegt, wird auf den Teil der Hyper­bolischen Spirale (blau) abgebildet, der außer­halb des Kreises liegt.

Eine Fermatsche Spirale, auch „Parabolische Spirale” genannt, ist eben­falls eine ebene Kurve, die sich in Polar­koordinaten durch die Gleichung einer Parabel beschreiben lässt.

Die Polardarstellung der Fermatschen Spirale ist definiert als:

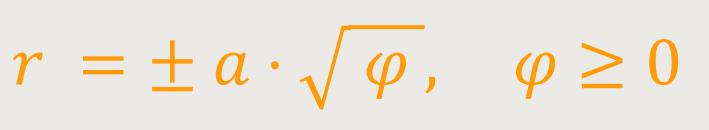
Die Fermatsche Spirale lässt sich in kartesischen Koordinaten ( x = r · cos φ, y = r · sin φ ) durch die Parameter­darstellung beschreiben:

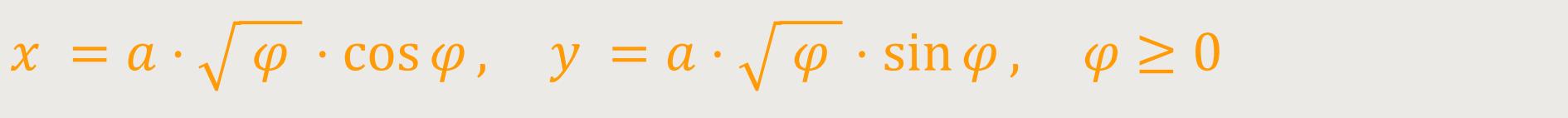
Aus obiger Parameter­darstellung und

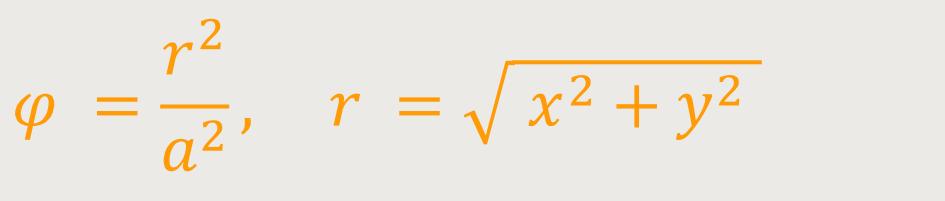
ergibt sich eine Darstellung mit der Gleichung:

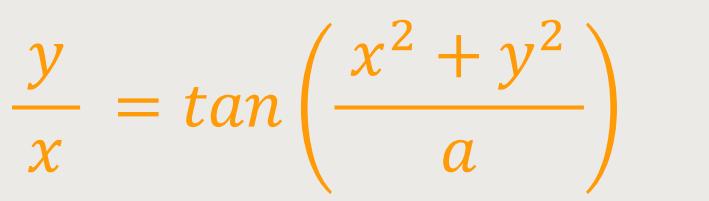
Die Fermatsche Spirale ähnelt der Archime­dischen Spirale. Aber im Gegensatz zu letzt­genannter hat die Fermatsche Spirale einen abneh­menden Windungs­abstand. Das heißt, die Windungen liegen nach außen hin immer dichter beieinander.

Abb. 3: Fermatsche Spirale (rechtsdrehend)

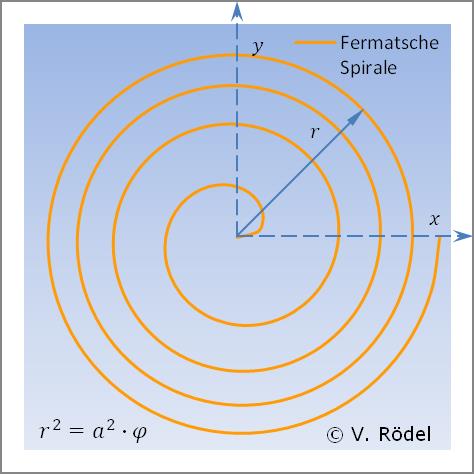
Die Fermatsche Spirale heißt auch deshalb „Parabolische Spirale”, da ihre Polar­gleichung eine Parabel beschreibt.

Die Krümmung k einer Kurve in Polar­darstellung ist definiert als:

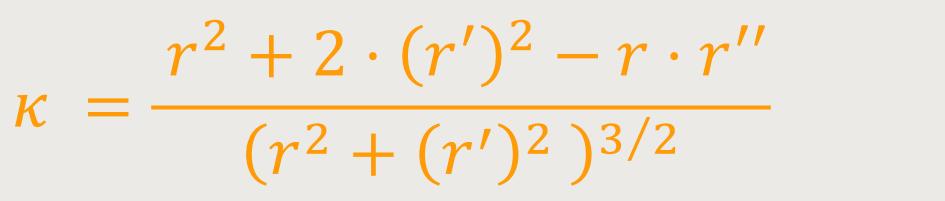
Für die Krümmung einer Kurve in Polar­darstellung r = r(φ) und den Ableitungen der Fermatschen Spirale

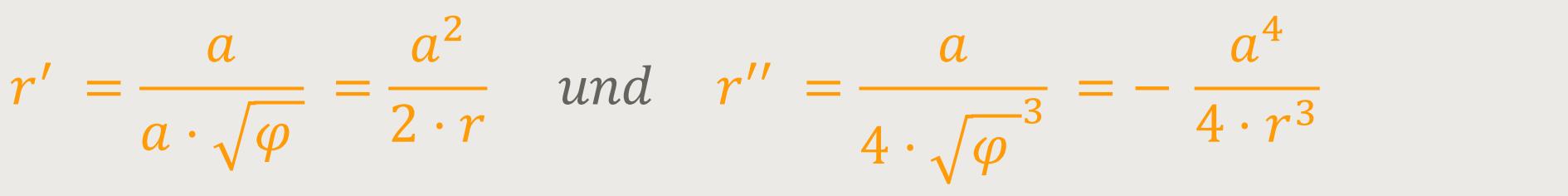
ergibt sich die Krümmung:

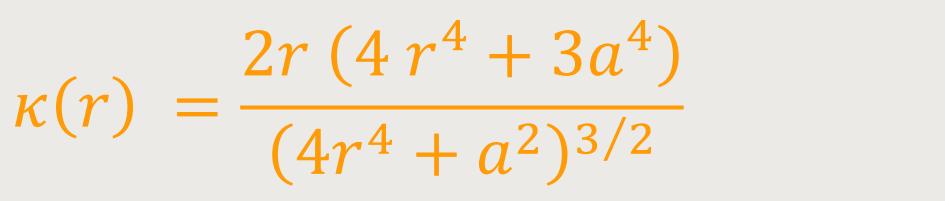
Im Nullpunkt ist die Krümmung Null. Die voll­ständige Spirale hat somit im Null­punkt einen Wende­punkt mit der x-Achse als Wende­tangente.

Die Spiegelung am Einheits­kreis (Inversion) lässt sich in Polar­koordinaten beschreiben durch:

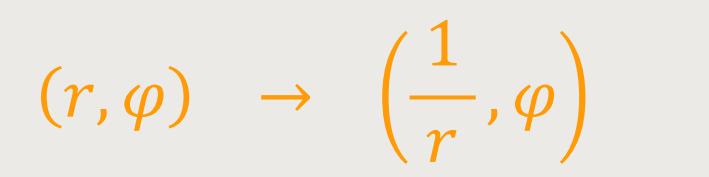
Insofern ergibt sich als grafische Darstellung der Fermatschen Spirale bei der Spiegelung am Einheits­kreis die Lituus-Spirale.

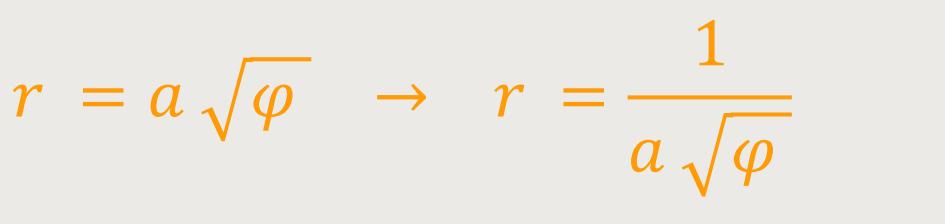
Für φ = 1/a² schneiden sich beide Kurven in einem Fixpunkt auf dem Einheits­kreis.

Die Wende­tagente (x-Achse) der Fermatschen Spirale (im Null­punkt) geht bei der Spiegelung in sich über und ist die Asymptote der Lituus-Spirale.

Abb. 4: Inversion der Fermatschen Spirale

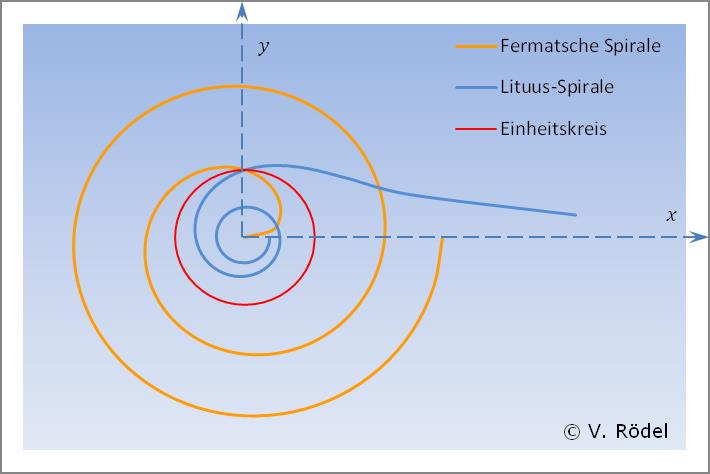
In der Mathe­matik ist eine Lituus-Spirale eine ebene Spirale, bei der der Winkel θ (Darstellung als Polar­koordinaten) umgekehrt propor­tional ist zum Quadrat des Radius r .

Die Polar­darstellung der Lituus-Spirale ist definiert als:

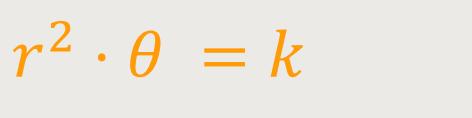
Die Lituus-Spirale, bei der beide Zweige vom Vorzeichen des Radius r abhängen, ist asymptotisch zur x-Achse. Ihre Wende­punkte liegen bei:

Abb. 5: Lituus-Spirale (rechtsdrehend)

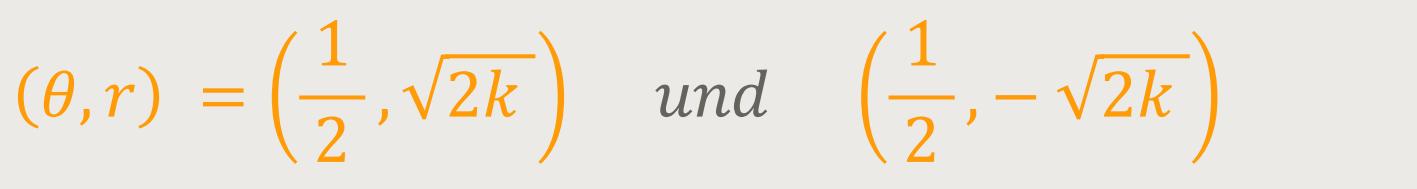
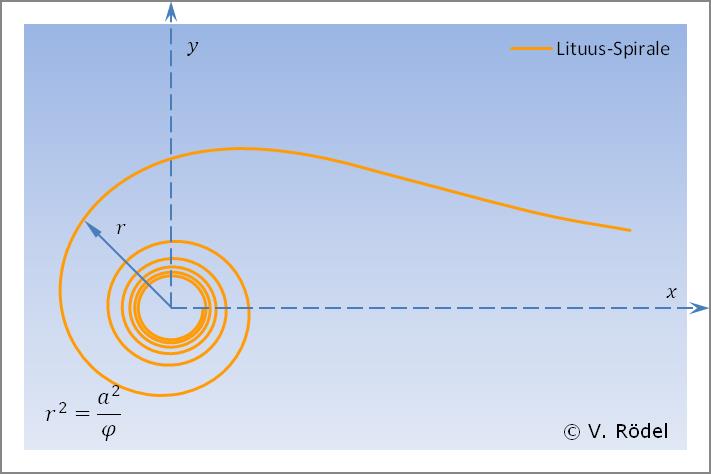
Die Lituus-Spirale ist das Bild einer Fermatschen Spirale bei einer Kreis­spiegelung.

Ein Vergleich obiger Spiralen mit den Wachstums­mustern in der Natur zeigt, dass die Logarith­mische Spirale aus dem vorherigen Kapitel am ehesten geeignet scheint, die Natur abzu­bilden. Doch bevor wir eine abschließende Aussage treffen, möchten wir einige Facetten der Goldene-Spirale näher untersuchen. Eine nähere Betrachtung lohnt sich, weil wir auf verschiedene kosmo­logische Zusammen­hänge stoßen werden.

⇦ Kapitel Kapitel ⇨