Der Begriff Goldener Schnitt spielt immer dann eine Rolle, wenn es um das Thema Schön­heit geht. Zum Beispiel die Schön­heit beim Betrachten eines Gesichtes. Oder die Schön­heit bei den Propor­tionen eines Autos oder eines Gebäudes. Wenn man beschreiben soll, was Schön­heit ist, können wir das meistens nicht in Worten aus­drücken. Wahre Schön­heit lässt sich nicht auf einige wenige Merkmale reduzieren. Daher hat man fast den Eindruck, dass es ein subjektives Empfinden ist, was jedem Menschen innewohnt.

Wenn der Begriff Schön­heit etwas Einheit­liches wäre, würden wir uns wahr­scheinlich alle gleich anziehen, wir würden die gleichen Autos fahren, oder noch schlimmer, wir würden uns in den gleichen Typ Mann oder Frau ver­lieben. Es gibt nicht umsonst die Rede­wendung: „Über Geschmack lässt sich nicht streiten.” Natürlich gibt es gewisse Vorlieben oder bestimmte Schönheits­ideale. Aber was im Mittel­alter als schön und ästhetisch empfunden wurde, mag heute nur noch wenige ansprechen.

Untersuchungen haben gezeigt, dass es oftmals ähnliche Empfin­dungen gibt für das, was wir als schön oder hässlich empfinden. Das zeigt sich besonders deutlich bei Gesichtern. Wir schauen als erstes dem Menschen ins Gesicht. In den ersten Sekunden entscheidet unser Unter­bewusstsein, ob wir den Gesprächspartner als sympathisch oder unsympathisch betrachten. Meistens sind es wohl­geordnete Proportionen, die wir als schön empfinden. Gesichter mit Unregel­mäßig­keiten empfinden wir dagegen eher als nicht schön. Alles, was eine ausgeprägte Symmetrie aufweist, wird als besonders schön empfunden.^[1]

Auf den ersten Blick scheinen wir den Begriff Schön­heit mit der Eigen­schaft der Symmetrie zu verbinden. Viel­leicht liegt es daran, dass wir in der Natur zahl­losen symme­trischen Struk­turen begegnen. Wir begegnen ihr bei der Form der Blätter, der Anordnung der Blüten, der Fell­zeichnung der Tiere, den Schmetterlings­flügeln usw. Aber Symmetrie hat keine ein­heitliche Erscheinungs­form. Es gibt zum Beispiel neben der Spiegel­symmetrie auch die Dreh­symmetrie, oder die Kugelsymmetrie.

Bei genauer Betrachtung stellt man jedoch fest, dass nichts genau symmetrisch ist. Wir ideali­sieren die Form und suchen unbewusst nach geome­trischen Mustern. Wir verbinden mit Symmetrie Schönheit, weil sie für eine gewisse Harmonie steht. Egal ob es im Mikro­kosmos oder im Makro­kosmos ist, man kann ihr überall begegnen.

Symmetrie folgt demnach bestimmten geometrischen Gesetzen, die verblüffend präzise sind. Diese Gesetze scheinen auch in unserem Bewusst­sein verankert zu sein. Doch obwohl wir wissen, dass sich beide Spiegel­hälften nicht aufs Haar gleichen, empfinden wir das Gesamt­bild als schön. Es ruft in uns ein gewisses Gefühl der Voll­kommen­heit hervor. Alles, was dagegen von der Norm abweicht, empfinden wir im ersten Moment als störend und unharmonisch. Bei genauerer Betrachtung stellen wir aber fest, dass ein Leber­fleck auf einer Gesichts­hälfte trotz­dem einen gewissen Lieb­reiz ausübt. Erst wenn wir uns von der Ober­flächlich­keit lösen, und die Indivi­dualität des Menschen erkennen, empfinden wir plötz­lich das Anders­artige als sympa­thisch und schön. Jemand sagte mal: „Schönheit ist quasi die augen­fällige Symmetrie mit einer Pointierung der Asymmetrie.”

Man hält es kaum für möglich, aber das Prinzip der Ungleich­heit spielt wie das Prinzip der Symmetrie eine funda­mentale Rolle. Asymmetrie scheint ebenfalls ein über­geordnetes Entwicklungs­muster im Kosmos zu sein. Lange Zeit galt innerhalb der Physik die Symmetrie der Elementar­teilchen als ein Grund­prinzip. Dieses Standard­modell musste jedoch 1957 mit dem Nach­weis asymme­trischer Verfalls­produkte von Kobalt 60 endgültig umgestürzt werden: In dem damaligen Experiment (Wu 1959) beobachtete man den Zerfall von Kobalt zu Nickel. Es entstanden entgegen der Vermutung mehr rechts­händige als links­händige Elektronen.

Im Jahr 1999 wies schließ­lich ein inter­nationales Wissen­schaftler­team (KTeV Collaboration 1999) am Fermi National Accelerator Laboratory die sogenannte direkte CP-Verletzung nach, die schon seit den sechziger Jahren theoretisch vermutet wurde. Beim Zerfall eines Kaons bzw. K-Meson, der Einheit eines Elementar­teilchens und seinem Anti­teilchen, entstanden erstmals asymme­trische Zerfalls­produkte. Es handelt sich um ein bis heute unerklärtes Phänomen. Mit dieser Erscheinung versucht man auch das Rätsel zu lösen, warum nach dem vermeint­lichen Urknall mehr Materie als Anti­materie übrig geblieben ist. Dieses enorme Ungleich­gewicht von Materie und Anti­materie im Kosmos ist die größte uns bekannte Asymmetrie überhaupt.

Oder nehmen wir unser Gehirn. Mittler­weile ist bekannt, dass die als funktionale Asymmetrie bezeichnete Gestaltung des mensch­lichen Gehirns Voraus­setzung für die Aus­bildung der indivi­duellen Fähig­keiten, Eignungen und Neigungen ist. Schon in einem frühen Stadium während der Embryonal­entwick­lung wird die ursprüng­liche Symmetrie des Embryos durch asymme­trische Genaktivi­täten gebrochen. Die unter anderem dadurch entstehende anatomische und vor allem funk­tionelle Ungleich­heit der beiden Großhirn­hemis­phären ist der wesent­liche Faktor für mensch­liche Intelligenz.^[2]

Während die Symmetrie ein Ideal hinter den tatsäch­lichen Formen ist, ist die Asymmetrie etwas Reales. Wenn wir von Propor­tionen und ihrem Ver­hältnis sprechen, geht es im Wesent­lichen um ein asymme­trisches Ver­hältnis von Teilen. In der Musik ist es das Verhältnis von Tönen, in der Malerei und Bild­hauerei das Ver­hältnis von Propor­tionen. Weil gewisse Propor­tionen als besonders schön und harmonisch empfunden werden, spricht man deshalb auch vom Goldenen Schnitt.

Wenn man zum Beispiel eine Strecke in zwei unter­schiedlich lange Teil­stücke aufteilen möchte, gibt es unend­lich viele asymme­trische Teilungs­möglichkeiten. Trotzdem gibt es nur „eine” Unter­teilung, die für den Betrachter als ästhetisch empfunden wird.

In obigem Beispiel teilt man eine Strecke so in zwei Teile, dass sich anschließend der kleinere Teil (Minor) zum größeren Teil (Major) genauso verhält, wie der größere Teil wiederum zum Ganzen. Es handelt sich somit um eine Teilung, bei der immer ein Bezug auf das Nächst­größere und somit schließ­lich auf das Ganze besteht. Gerade durch die Teilung wird der Bezug zum Ganzen heraus­gestellt. Auf diese Weise schafft es der Goldene Schnitt die Zer­störung der Strecke im Kontext zum Ganzen wieder zu vereinen.

Es gibt eine geome­trische Form, die den Goldenen Schnitt in Perfektion wider­spiegelt: Das Pentagramm. Nicht ohne Grund wurde ihm zu allen Zeiten eine magische Wirkung zugeschrieben.

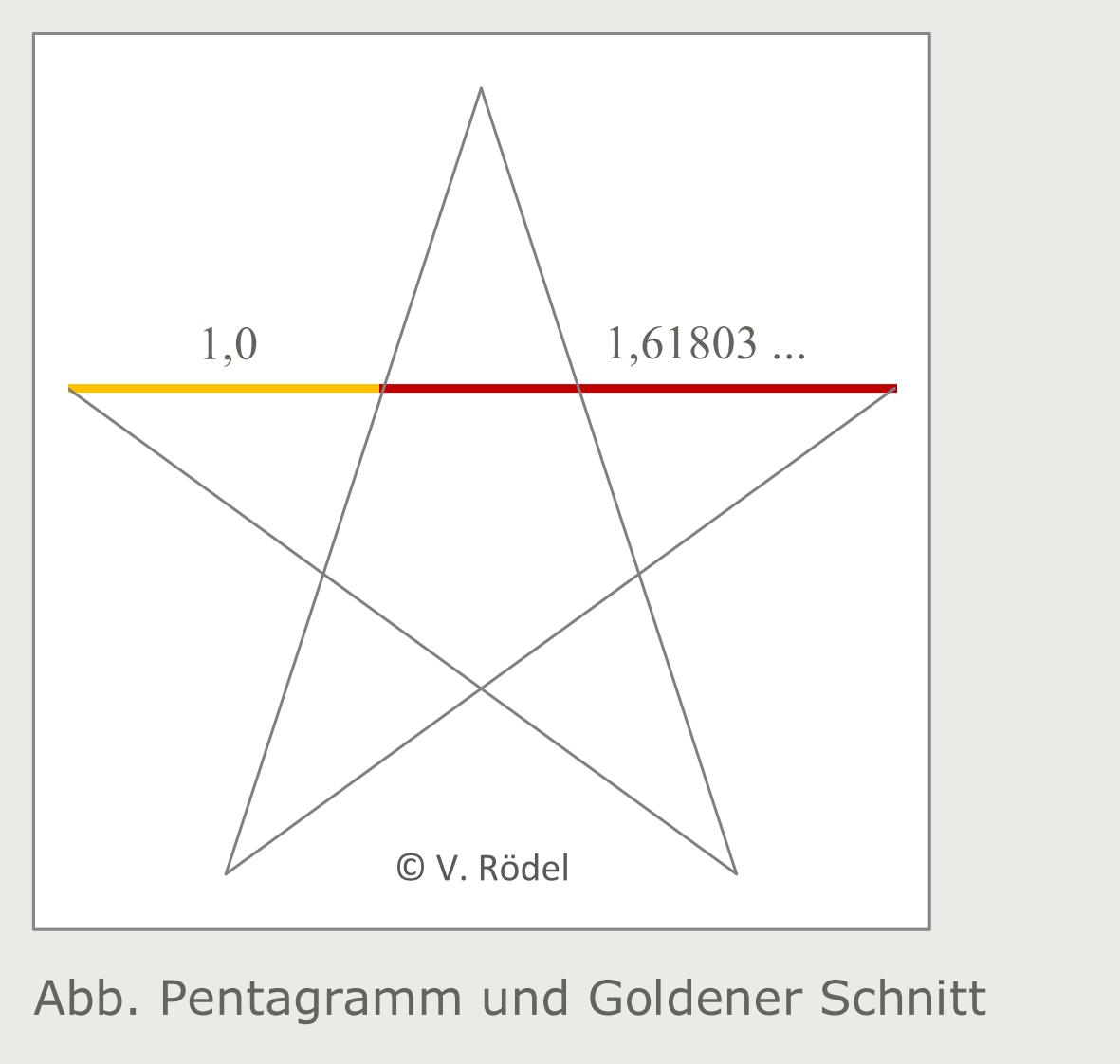
Abb. Das Pentagramm und der Goldene Schnitt

Es ist also nicht mehr die Gleich­heit der Teile, sondern die Gleich­heit der Propor­tionen, die eine Faszi­nation ausübt. Die Verhält­nisse der Teile „Minor zu Major” und „Major zum Ganzen” sind immer gleich. Dadurch ist im Goldenen Schnitt das Verhältnis jetzt symmetrisch. Die Symmetrie der Teile wird vorder­gründig zu Gunsten der Symmetrie der Propor­tionen geopfert. Und dennoch findet sich selbst im Goldenen Schnitt die Symmetrie der Teile wieder.

Der Goldene Schnitt verbindet so auf beein­druckende Weise das Prinzip der Symmetrie mit dem der Asymmetrie. Diese Gesetz­mäßig­keit hat man auch als „göttliche” Propor­tion bezeichnet. Sollte viel­leicht doch eine göttliche Intel­ligenz hinter diesem Zusammen­hang stehen?

Rechnet man das Verhältnis zwischen „Minor zu Major” aus, und „Major wiederum zum Ganzen”, so ergibt sich daraus eine unend­liche Zahl. Diese Zahl Φ (Phi), gehört zu den Natur­konstanten und wird angegeben mit: Φ = 1,61803.... Erstaun­licher Weise ist es gerade ein irratio­nales Zahlen­verhältnis, dass als besonders harmonisch und schön empfunden wird.

Vor rund 160 Jahren beschäftigte sich der Mediziner Adolf Zeising mit den Maßen des mensch­lichen Körpers. Die Ergebnisse veröffent­lichte er in seinem Lebens­werk Neue Lehre von den Propor­tionen des mensch­lichen Körpers (1854). Wird zum Beispiel der untere Teil des mensch­lichen Körpers als „Major” und der obere als „Minor” angenommen, so verläuft die Trennungs­linie beider Abschnitte in der Höhe des Bauch­nabels. Bei der Teilung des Ober­körpers im Goldenen Schnitt stellt sich die Trennungs­linie in Höhe des Kehl­kopfes dar. Im Unter­körper fällt die Trenn­linie nicht genau durch das Knie­gelenk, sondern knapp unter der Knie­scheibe. Hier gibt es eine optische Einbuchtung, ähnlich der Einbuchtung der Hüfte oder des Halses.

Zeising hat die Propor­tionen des Goldenen Schnittes bis ins kleinste Detail am mensch­lichen Körper aufgezeigt. Die anatomische Genauig­keit dieses Verhält­nisses bei der Gliederung des Menschen ist äußerst beeindruckend. So hat man auch bemerkt, dass die Breiten der ersten beiden oberen Schneide­zähne im Verhältnis 1 : 1,61803... stehen. Wie der Goldene Schnitt an sich, so ist auch der Mensch Ausdruck von Symmetrie und Asymmetrie.

Der Goldene Schnitt zeigt sich jedoch nicht nur am mensch­lichen Körper. Im Laufe des 19. und 20. Jahrhunderts konnte er auch in zahl­reichen Wachstums­mustern von Pflanzen und Tieren nach­gewiesen werden. Dazu mehr im nächsten Kapitel.

Quellen

[1] Bates & Cleese 2001
[2] Eckert & al. 2003

⇦ Kapitel Kapitel ⇨