Die Botaniker Alexander Braun und Carl Schimper untersuchten ab den 1830er Jahren zum Beispiel die Wachstums Geometrien in der Pflanzenwelt. So fanden sie heraus, dass die Abfolge der Blätter am Stängel einer Pflanze teils eine symmetrische und teils eine spiralige Blattstellung aufweisen. Bei der symmetrischen Anordnung stehen sich jeweils zwei Blätter gegenüber. Bei der asymmetrischen Blattstellung sind die einzelnen Blätter wie eine Spirale angeordnet. [x]
Interessanter Weise spricht man deshalb auch neben dem Goldenen Schnitt vom Goldenen Winkel. Er weist die gleichen bemerkenswerten Besonderheiten auf.
Bei den meisten Pflanzen bilden sich neue Organe wie Stängel, Blätter und Blüten von einem winzigen zentralen Vegetationspunkt aus, dem Meristem oder Bildungsgewebe. Von diesem Zentrum aus wächst jede neue Anlage der Pflanze in eine andere Richtung, und zwar in einem bestimmten Winkel zur vorherigen Anlage. Bei den meisten Pflanzen werden die neuen Anlagen in einem ganz speziellen Winkel angelegt, durch den schließlich ein Spiralmuster entsteht. Was ist das für ein Winkel?
Stellen wir uns vor, man müsste eine Pflanze entwerfen, deren Anlagen so dicht um den Vegetationspunkt gruppiert sein sollen, dass keinerlei Platz verloren geht. Angenommen, man würde sie so konstruieren, dass sich beispielsweise immer nach zwei Fünfteln einer Drehung eine neue Anlage bilden würde (als Bruch ausgedrückt: 2/5). In diesem Fall würde jede fünfte Anlage wieder direkt über dem Ausgangspunkt entstehen und in die gleiche Richtung wachsen. Auf diese Weise entstünden zwar Reihen, aber man hätte das Problem, dass zwischen den Reihen Lücken auftreten, und damit Platz verloren geht. Das Problem würde sich über die ganze Pflanze aufsummieren, denn bei jeder Drehung, die sich in Form eines einfachen Bruchs ausdrücken lässt, entstünden Reihen bei denen der Platz nicht optimal genutzt wird. Nur bei einer Drehung im Goldenen Winkel von ungefähr 137,5° sind die Anlagen optimal dicht und absolut Platz sparend angeordnet. Wieso ist gerade dieser Winkel so ideal?
Der Goldene Winkel lässt sich nicht als Bruch aus ganzen Zahlen darstellen.
Der Bruch 5/8 einer Umdrehung kommt annähernd an diesen Winkel
heran, 8/13 noch näher und 13/21 nochmals
näher. Diese Brüche kennen wir bereits aus der Fibonacci-Folge.
Interessanterweise lässt sich der Winkel, der einen Kreis im Maßverhältnis
des Goldenen Schnitts teilt, durch keinen einfachen Bruch exakt ausdrücken. Das
bedeutet:
Wenn sich eine neue Anlage jedes Mal in diesem bestimmten Winkel zur vorherigen
ausbildet, stehen niemals zwei Anlagen genau übereinander. Auf diese Weise bilden sie
nicht strahlenförmige Arme, sondern Spiralen.
Jedes Blatt an einer Pflanze bildet zum nächst höheren somit einen bestimmten Winkel (Divergenz). Folgt man der Anordnung der Blätter, so wird man spiralig um den Stiel herumgeführt. Erst ein ganz bestimmtes Blatt zeigt dann annähernd wieder in die gleiche Richtung wie das erste Blatt. Bis zu dieser Ausgangsstellung wird eine bestimmte Anzahl von Windungen zurückgelegt. Dies wird als Blattzyklus bezeichnet und in Bruchzahlen angegeben. Winden sich beispielsweise fünf Blätter in zwei Windungen um den Stiel bis die Ausgangsstellung wieder erreicht ist, dann spricht man von einem Blattzyklus von 2/5. Eine Computersimulation ergibt, dass das Spiralmuster nur dann erkennbar ist, wenn sich die Anlagen vom Vegetationspunkt aus mit großer Genauigkeit im Goldenen Winkel zum Vorgänger ausbilden. Bei einer Abweichung von nur einem Zehntel Grad verliert sich der Spiraleffekt.
Hinter der offensichtlich asymmetrischen Blattanordnung verbirgt sich dennoch wieder eine Regelmäßigkeit, eine Symmetrie.
Im Pflanzenreich kommen verschiedene Arten von Blattzyklen vor, wobei einige besonders oft auftreten. Trägt man das gesamte Spektrum der verschiedenartigen, tatsächlich in der Natur vorkommenden Blattzyklen zusammen, so entsteht folgende Reihe:
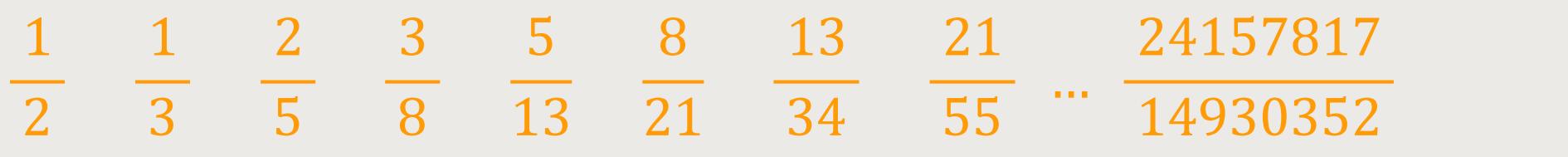
1/2 – 1/3 – 2/5 –
3/8 – 5/13 – 8/21 –
13/34 – 21/55 …
Es handelt sich bei der Zahlenreihe sowohl im Nenner als auch im Zähler jeweils um Zahlen, die wir als die Fibonacci-Folge kennengelernt haben, nur lediglich um zwei Stellen verschoben.
Bezogen auf den Vollkreis ergeben sich nachfolgende Winkel. Je größer die Zahlen im Zähler und Nenner werden, desto weiter nähert sich das Verhältnis dem Goldenen Winkel an.
| Nr. | Verhältnis | Winkel | 1 | 1 / 1 | 360,000000° |
|---|---|---|
| 2 | 2 / 1 | 180,000000° |
| 3 | 3 / 2 | 120,000000° |
| 4 | 5 / 3 | 144,000000° |
| 5 | 8 / 5 | 135,000000° |
| 6 | 13 / 8 | 138,461538° |
| 7 | 21 / 13 | 137,142857° |
| 8 | 34 / 21 | 137,647059° |
| 9 | 55 / 34 | 137,454545° |
| 10 | 89 / 55 | 137,528090° |
| 11 | 144 / 89 | 137,500000° |
| 12 | 233 / 144 | 137,510730° |
| 13 | 377 / 233 | 137,506631° |
| 14 | 610 / 377 | 137,508197° |
| 15 | 987 / 610 | 137,507599° |
| 16 | 1597 / 987 | 137,507827° |
| 17 | 2584 / 1597 | 137,507740° |
| 18 | 4181 / 2584 | 137,507773° |
| 19 | 6765 / 4181 | 137,507761° |
| 20 | 10946 / 6765 | 137,507765° |
| 21 | 17711 / 10946 | 137,507763° |
| 22 | 28657 / 17711 | 137,507764° |
| ... | ... | ... |
Zum besseren Verständnis sei erwähnt, den Goldenen Winkel erhält man, wenn der Vollwinkel im Goldenen Schnitt geteilt wird.
Das führt zunächst auf den überstumpfen Winkel:

In der Regel wird aber dessen Ergänzung zum Vollwinkel als Goldener Winkel bezeichnet:

Das hängt damit zusammen, dass Drehungen um ±2π keine Rolle spielen und das Vorzeichen nur den Drehsinn des Winkels angibt. Wie bei jeder irrationalen Zahl wird es auch hier nie zu exakten Überdeckungen der Blätter kommen, sodass jedes Blatt genügend Licht erhält und damit die Photosynthese mit einer unschlagbaren Effizienz abläuft. Man könnte fast sagen mit einer Energieausbeute von 100%.
Für den Goldenen Winkel ergibt sich somit die unendliche Maßzahl von 137,50776405…°.
Setzt man zudem den Kehrwert von Zähler und Nenner ins Verhältnis, ergibt
sich zum Beispiel bei
Diese Einzigartigkeit des Goldenen Schnitts und des Goldenen Winkels lässt sich auch in der Goldenen Spirale wiedererkennen. Mit ihr nähern wir uns immer mehr dem alles erklärenden Naturgesetz. Um ein besseres Verständnis für die Goldene Spirale zu erhalten, wollen wir zuvor die gängigsten Spiralkurven und ihren Besonderheiten noch etwas näher betrachten.
Sie lassen sich in zwei Gruppen einteilen: In die „ebenen” (flachen) Spiralkurven und die „räumlichen” Spiralkurven. Letztere spielen besonders bei dynamischen Strukturen bzw. Wachstumsprozessen eine wesentliche Rolle.
⇦ Kapitel Kapitel ⇨
