In diesem Teil werden wir die Räum­lichen Spiralen noch um einige Varianten vervoll­ständigen.

Die nach­folgenden Spiralen lassen sich theoretisch auch auf einem „Kreis­kegel” abbilden. Allerdings würde dadurch der wahre Zweck dieser Spiralen verfälscht. Denn die tatsäch­liche Projektion muss auf einem hyper­bolischen Körper erfolgen.

Eine Spirale auf Basis der „Hyperbolischen Spirale” lässt sich beschreiben als:

Abb. 1: Hyperbolische Spirale (rechts­drehend; in negativer Richtung zunehmend)

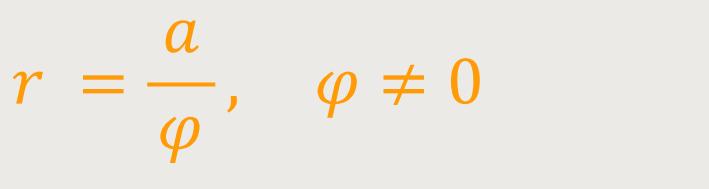
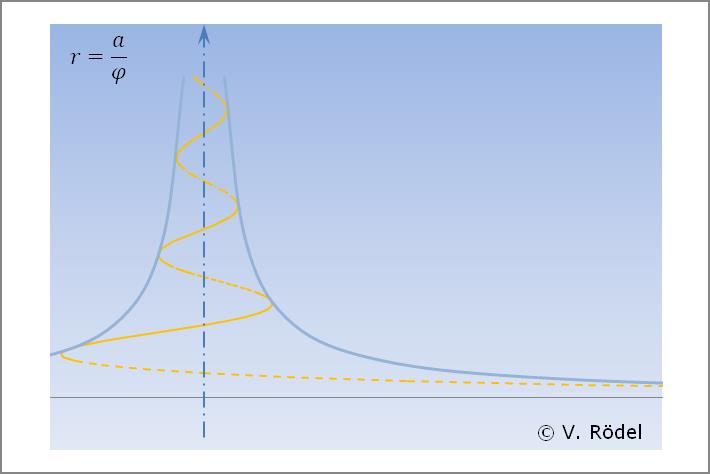
Würde man auch hier eine konische Projektion wählen, erhielte man einen viel steiler verlau­fenden Kurven­verlauf. Grund­sätzlich ist zwar interessant, dass diese Spirale dann eine Asymptote besäße, dessen Grund­riss eine Hyperbel bildet, an welche sich die konische Spirale für φ > 0 annähert. Doch mit diesem Lösungs­ansatz kämen wir bei unserer Betrachtung nicht weiter. Daher müssen wir obige grafische Darstellung zugrunde legen.

In der Mathe­matik ist eine „Lituus-Spirale” eine Spirale, bei der der Winkel θ (Darstellung als Polar­koordinaten) umgekehrt propor­tional ist zum Quadrat des Radius r.

Die Polardar­stellung der Lituus-Spirale ist definiert als:

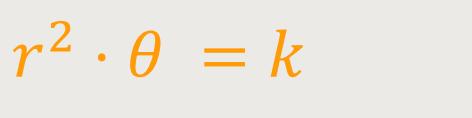
Sie hat ebenfalls hyperbo­lischen Charakter und lässt sich beschreiben als:

Abb. 2: Lituus Spirale (rechts­drehend; in negativer Richtung zunehmend)

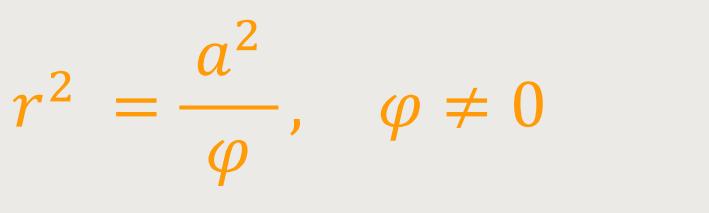
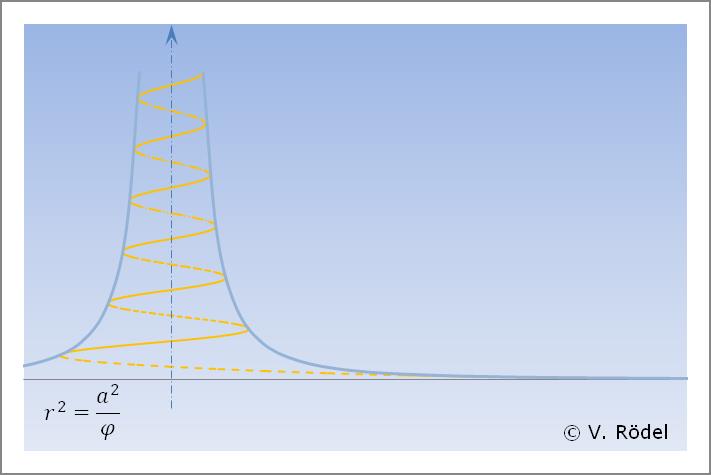
In der weiteren Betrachtung wird die hyperbo­lische Spirale eine über­geordnete Rolle spielen. Mit ihr lassen sich Wirbel­strukturen in unserem Sonnen­system nach­weisen, wobei sich diese letzt­lich sogar auf Galaxien bis hin zum Aufbau des gesamten Universums über­tragen lassen.

⇦ Kapitel Kapitel ⇨