Die „Kosmos-Spirale” entspricht einem Kurvenverlauf, der einen physikalischen bzw. kosmologischen Grenzwert beschreibt. Es ist der gleiche Kurvenverlauf, wie ihn Photonen vollziehen, wenn sie in ein Schwarzes Loch hineinspiralen. Die Spirale umkreist den Mittelpunkt, ohne ihn zu erreichen. Man bezeichnet dies auch als asymptotischen Punkt.
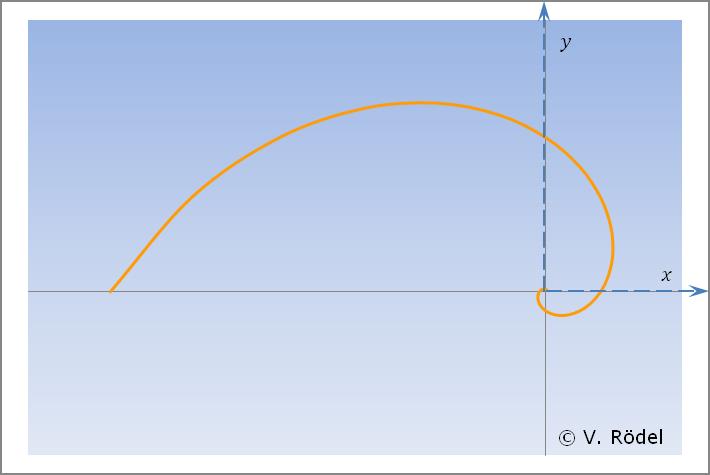
Wie in den vorherigen Kapiteln anschaulich illustriert wurde, werden alle Spiralkurven durch die Steigung und die Krümmung der Kurve beschrieben. Entsprechend der gewählten Winkeleinteilung lässt sich jeder Knotenpunkt als Übergang von einem Kurvensegment zum nächsten grafisch darstellen.
Die Winkeleinteilung kann zwar willkürlich gewählt werden, aber sie sollte vorzugsweise auf das Energiepotential abgestimmt sein, um den optimalen grafischen Effekt zu erzielen.
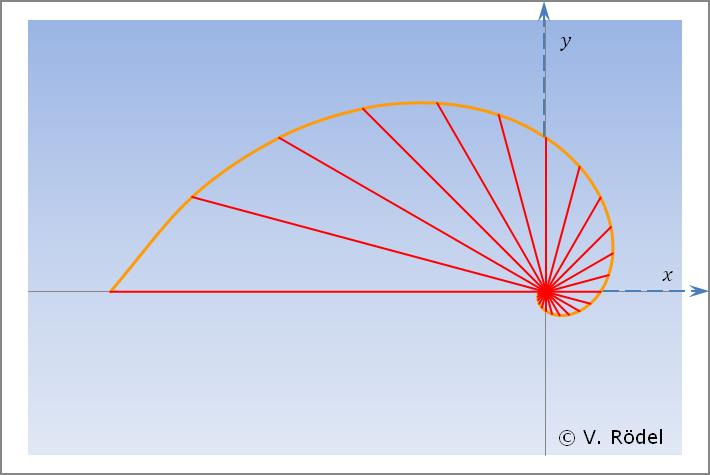 Abb. 2: Kosmos-Spirale (rechtsdrehend) mit den Sehnen
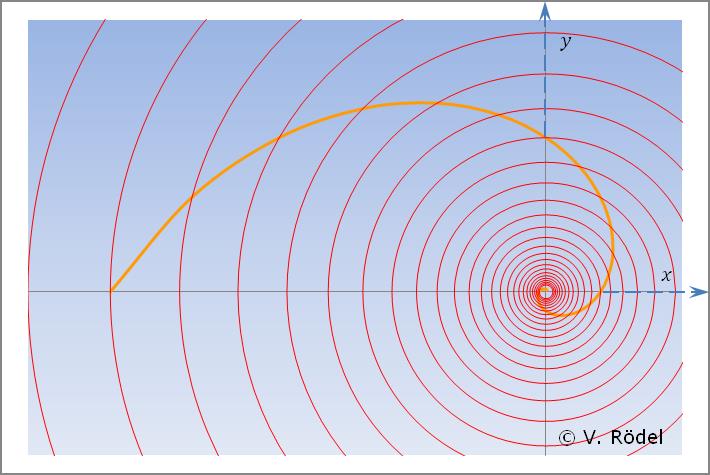
Abb. 2: Kosmos-Spirale (rechtsdrehend) mit den Sehnen Jeder Knotenpunkt auf dem Kurvenverlauf der Spirallinie entspricht dem
Schnittpunkt eines konzentrischen Kreises, dessen Mittelpunkt im Zentrum des
Koordinatensystems liegt. Alle diese konzentrischen Kreise stellen sich
flächenmäßig so dar, dass die benachbarten Kreisflächen
genau um den Wert
Wie steil bzw. wie flach der hyperbolische Kegel verläuft, hängt maßgeblich vom Drehimpuls des jeweiligen Systems ab. Je höher die Geschwindigkeit, desto steiler bzw. langgezogener ist der in negative Richtung (wie hier) verlaufende Trichter. In der Kosmologie würde dies einem Schwarzen Loch entsprechen. Aus diesem Grund sind die Spiralgalaxien und auch unser Sonnensystem viel flacher, weil der Drehimpuls dieser Systeme nicht an den universellen Gesamtdrehimpuls heranreicht.
Wenn wir uns bei Geschwindigkeiten nahe der Lichtgeschwindigkeit bewegen, ist der Trichter extrem langgezogen. Aber entgegen landläufiger Vorstellung endet ein derartiger Trichter nicht im Nirgendwo, sondern es schließt sich ein gleichgearteter hyperbolischer Trichter auf der Gegenseite an und bildet dann in der Kosmologie ein „Weißes Loch”.
Die nachfolgende Grafik zeigt anschaulich wie die Energie und damit auch der elektromagnetische Fluss im Potential verläuft. Die magnetische Flussdichte nimmt ebenfalls bei höherer Geschwindigkeit zu.
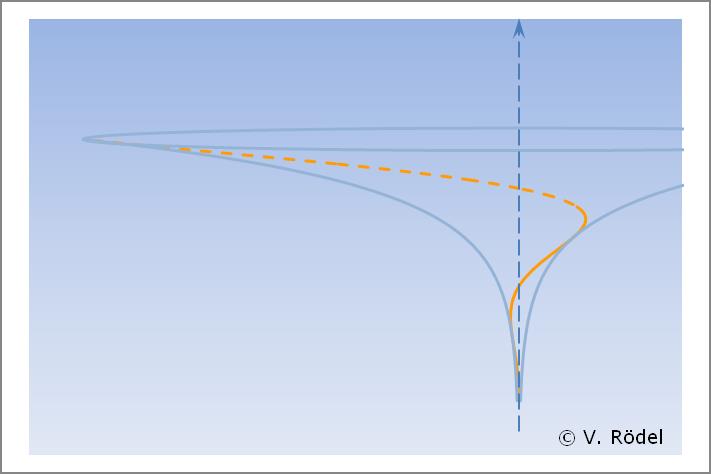
mit hyperbolischer Form (in y-Richtung gestaucht dargestellt)
Beschreibt man die Geschwindigkeit eines Teilchens beim Hineinspiralen in einen derartigen Potentialtrichter grafisch, so ergibt sich eine hyperbolische Kurve.
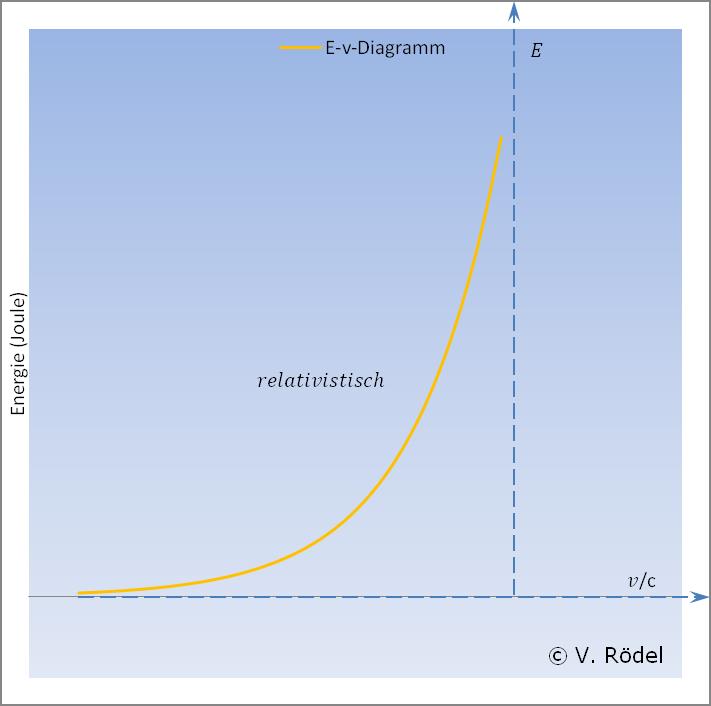
Bei zunehmender Geschwindigkeit nimmt auch die Energie entsprechend zu.
… Fortsetzung folgt.
⇦ Kapitel Kapitel ⇨
