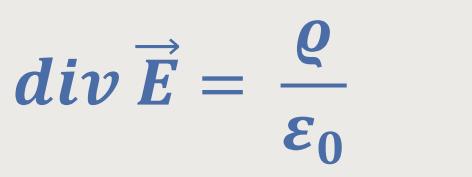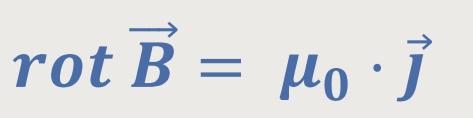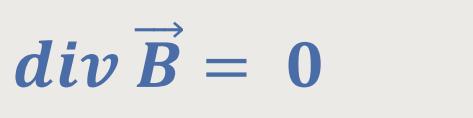Bisher haben wir 3 wichtige Beziehungen erarbeitet. Die erste Gleichung ergab sich aus der Ladungsverteilung in einem System und war definiert als:
Diese Beziehung besagt, dass die Ladungsdichte im Wesentlichen mit der Quelldichte des elektrischen Feldes identisch ist. Die gesamte Elektrostatik baut auf dieser Gleichung auf.
Die Lösung dieser Gleichung war mit nachfolgendem Potentialansatz möglich:
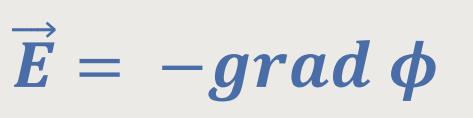
Durch Einsetzen in obige Beziehung erhält man eine skalare Differenzialgleichung für das elektrische Potential. Das geht natürlich nur, wenn das elektrische Feld ein konservatives Kraftfeld ist, und das ist in der Elektrostatik der Fall. Denn in zeitabhängigen Systemen gibt es keine konservativen Kraftfelder.
Bei der Betrachtung der magnetischen Kraftfelder wurde eine zweite Maxwell-Gleichung definiert:
Ein Vergleich mit der Elektrostatik zeigt, dass aus der Divergenz die Rotation wird, und aus der Ladungsdichte wird die Stromdichte. Mit dieser Gleichung wird das magnetische Kraftfeld in Anwesenheit von Strömen beschrieben.
Diese Beziehung besagt, dass die Stromdichte im Wesentlichen mit der Wirbeldichte
des magnetischen Feldes identisch ist. Ein magnetischer Feldwirbel wird
letztlich beschrieben durch das 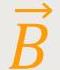 -Feld.
Und der Rotationsvektor liegt hierbei parallel zur Wirbelachse, wobei der Betrag
jeweils die Zirkulation rund um eine betrachtete Fläche angibt. Je größer
die Wirbeldichte ist, desto größer wird der Betrag von
rot
-Feld.
Und der Rotationsvektor liegt hierbei parallel zur Wirbelachse, wobei der Betrag
jeweils die Zirkulation rund um eine betrachtete Fläche angibt. Je größer
die Wirbeldichte ist, desto größer wird der Betrag von
rot 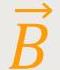 sein.
sein.
Die dritte Maxwell-Gleichung beschreibt den Sachverhalt, dass es keine magnetischen Monopole gibt:
Insofern quillt das Magnetfeld nirgendwo heraus. Vielmehr sind alle Magnetlinien geschlossen, und daher wird der Fluss aus einer derart geschlossenen Fläche heraus Null sein.
Wie bereits erwähnt, sind die ersten beiden Maxwell-Gleichungen inhomogen und die dritte dagegen homogen. Allerdings war die dritte Gleichung noch unvollständig. Außerdem gibt es noch eine weitere homogene Maxwell-Gleichung.
Ziel ist es jetzt, mit Hilfe der Maxwell'schen Grundgleichungen, aus den Stromdichteverteilungen die zugehörigen Magnetfelder zu gewinnen. Wie zum Beispiel das Magnetfeld in der Umgebung einer stromdurchflossenen Stromschleife bzw. einer Spule aussieht. Oder aber, wenn es nur darum geht, das Magnetfeld eines geradlinigen Stromleiters zu berechnen.
Hierzu gibt es das sogenannte „Biot-Savart-Gesetz”, welches es einem ermöglicht, bei beliebig geformten dünnen Stromleitern, die zugehörigen magnetischen Felder zu ermitteln. Um auf den grundsätzlichen Lösungsansatz zu kommen, ist es wieder notwendig, zuvor einen Potentialansatz zu machen. Hierbei geht es aber nicht um die potentielle Energie. Man erhält jetzt vielmehr eine vektorielle Größe, die als „Vektorpotential” bezeichnet wird.
Im vorherigen Kapitel hatten wir gesehen, dass die magnetische Spannung gleich dem Strom ist. Das heißt im Allgemeinen für das maßgebliche Ringintegral:
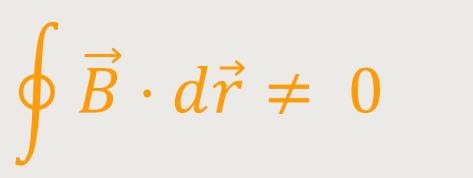
Das bedeutet, dass selbst im Fall der Magnetostatik, das magnetische Kraftfeld nicht konservativ sein wird. Deswegen lässt sich analog zur Elektrostatik hier kein Ansatz mit der Bildung des Gradienten machen. Denn es gibt gravierende Unterschiede zwischen beiden Gebieten.
Dennoch lässt sich mit Hilfe der homogenen Maxwell-Gleichung
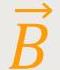 = 0
= 0
In der Vektoranalysis gibt es verschiedene Grundgleichungen, deren Kenntnis von Vorteil ist. Eine dieser Grundgleichungen lautet:

Weil das elektrostatische Feld ein konservatives Kraftfeld ist, ist die Rotation des elektrischen Feldes in der Elektrostatik gleich Null, und nur dann kann ein Ansatz mittels eines Gradienten gemacht werden.
Eine zweite dieser Grundgleichungen lautet:
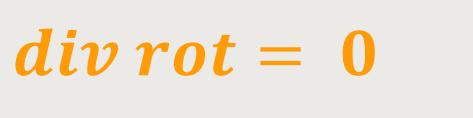
Mit dieser Beziehung lässt sich jetzt ein Ansatz für die dritte Maxwell-Gleichung machen, um diese weiter auszuformulieren. Wobei die Aussage der bisher formulierten dritten Maxwell-Gleichung grundsätzlich erhalten bleibt. Es lässt sich nun schreiben:

 ist das Vektorpotential
ist das Vektorpotential
Dieses Vektorpotential wird nachfolgend als Werkzeug verwendet, um die
Magnetfelder von Strömen zu berechnen. Die beiden Potentiale
ϕ (phi) und  sind in der Lage, die jeweiligen Kraftfelder darzustellen.
sind in der Lage, die jeweiligen Kraftfelder darzustellen.
Dabei ist interessant, dass das magnetische Vektorpotential
Jetzt haben wir das Vektorpotential eingeführt.
Das elektrische Potential ϕ (phi) ist aber noch nicht ganz
eindeutig. Denn wenn das ϕ um eine Konstante erweitert wird,
ändert das nichts an dem Gradienten, und daher auch nichts an dem elektrischen
 -Feld. Das bedeutet, das Potential
ϕ ist nicht klar definiert. Verschiedene Potentiale, die sich durch
Konstanten voneinander unterschieden, liefern jeweils das gleiche elektrische Feld.
-Feld. Das bedeutet, das Potential
ϕ ist nicht klar definiert. Verschiedene Potentiale, die sich durch
Konstanten voneinander unterschieden, liefern jeweils das gleiche elektrische Feld.
Wie sieht es aber mit dem magnetischen Potential
 aus? Wenn man auch hier eine gewisse
Konstante hinzufügt, und daraus ein
aus? Wenn man auch hier eine gewisse
Konstante hinzufügt, und daraus ein
 '
'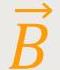 -Feld
-Feld eine größere Freiheit hat, sich zu verändern. Nämlich dadurch,
dass man noch einen Gradienten hinzufügen kann.
eine größere Freiheit hat, sich zu verändern. Nämlich dadurch,
dass man noch einen Gradienten hinzufügen kann.

Folgende Überlegung soll diesen Gedankengang verdeutlichen:
Bei vorgegebenem 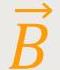 sei
sei
 ein Vektorpotential. Neben
ein Vektorpotential. Neben
 ist auch
ist auch
 ' =
' =
 + grad f(
+ grad f(
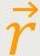 ) + const
) + const
Hinweis: Der Gradient wird bildet von einem Skalar und daraus wird dann wieder ein Vektor.
Wenn man jetzt eine Rotation von
 '
'

rot grad ist aber immer Null
rot const ist ebenfalls Null
Also bleibt nur mehr stehen:
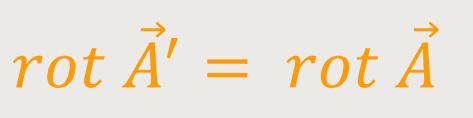
Damit erhält man die gleiche Aussage wie für das
 -Feld
-Feld
Auf diese Weise ergeben sich verschiedene Möglichkeiten, auf ein anderes
Potential zu transformieren, das anschließend wieder das richtige
 -Feld
-Feld
Wie lässt sich aber nun das Magnetfeld einer vorgegebenen Stromverteilung konkret ausrechnen?
Hierzu benötigen wir als Ausgangssituation wieder die inhomogene Maxwell-Gleichung:
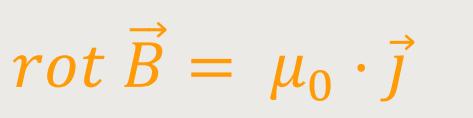
Wenn man entsprechend für 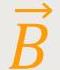 einsetzt, ergibt sich:
einsetzt, ergibt sich:
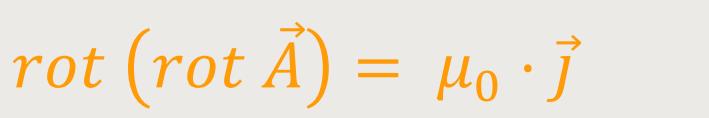
Laut einer der Grundgleichungen (Formelsammlung) kann man stattdessen auch schreiben:
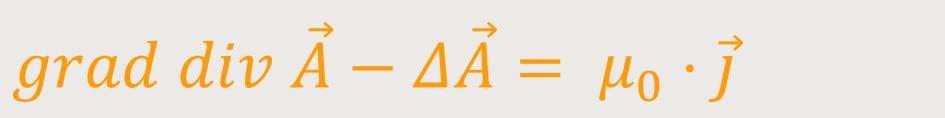
Nun kann man auf Gundlage der Vorgehensweise bei Eichtransformation entsprechend
erreichen, dass nicht nur
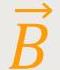 = rot
= rot

 = 0
= 0
Wenn es bei entsprechender Eichtransformation gelingt, dass div
 = 0 ist, dann wird der Gradient
davon auch Null sein. Insofern bleibt nur noch stehen:
= 0 ist, dann wird der Gradient
davon auch Null sein. Insofern bleibt nur noch stehen:
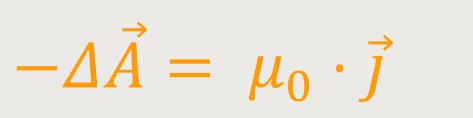
oder

Und das ist anlog zur Elektrostatik, wo galt:
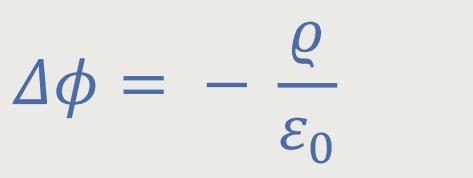
Abgesehen davon, das ϕ (phi) ein Skalar ist, und
 ein Vektor, gibt es eine Analogie
zwischen der Elektrostatik und der Magnetostatik. Und wenn beides miteinander
verknüpft wird, erhält man, wie bereits erwähnt, einen
ein Vektor, gibt es eine Analogie
zwischen der Elektrostatik und der Magnetostatik. Und wenn beides miteinander
verknüpft wird, erhält man, wie bereits erwähnt, einen
Und für einen stromfreien Raum (z.B. Vakuum) gilt dann:

In der Elektrostatik entspricht das der Laplace-Gleichung:

Jetzt möchten wir obige Gleichung
 = −
μ₀ ·
= −
μ₀ · 

Nun wird diese Beziehung mit obiger Laplace-Gleichung verglichen, wodurch man eine Entsprechung findet, die sich wie folgt darstellt:
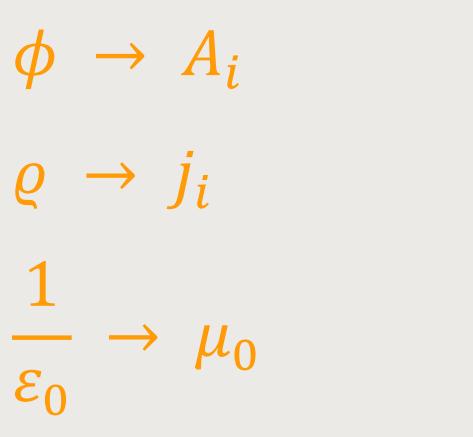
Wenn man diese drei Komponenten entsprechend ersetzt, kann man einfach die Lösung der Poisson-Gleichung aus der Elektrostatik in die Magnetostatik übertragen. Denn das sind strukturell gesehen die gleichen Beziehungen, und daher auch die Lösungen entsprechend.
Hierzu verwendet man einfach die bereits erarbeitete Lösung aus der Elektrostatik. Man kann sich eine Ladungsverteilung in Form einer Anzahl von vielen Punktladungen Qi denken.
Dann ergibt sich als Lösung für die Poisson-Gleichung:
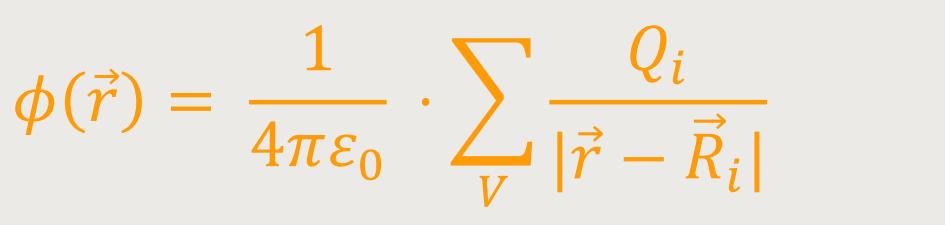
Grafik (wird später eingefügt)
Man betrachtet einen gewissen Bereich, in welchem eine bestimmte Anzahl von Punktladungen
Qi enthalten sind. Der Ortsvektor vom Ursprung zu
einer dieser Punktladungen bezeichnet man mit
 i.
Ein Beobachter befindet sich im Aufpunkt P, der seinerseits vom
Ursprung durch den Ortsvektor r beschrieben wird. Demnach ist der
Verbindungsvektor von der Punktladung zum Aufpunkt
i.
Ein Beobachter befindet sich im Aufpunkt P, der seinerseits vom
Ursprung durch den Ortsvektor r beschrieben wird. Demnach ist der
Verbindungsvektor von der Punktladung zum Aufpunkt
 −
− i.
i.
Für eine kontinuierliche Ladungsverteilung, bei der in einem Volumen für
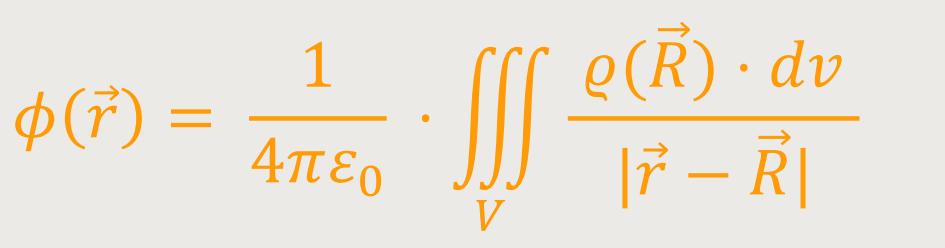
Analog erhält man jetzt durch Ersetzen (siehe Entsprechung) für ein Magnetfeld:
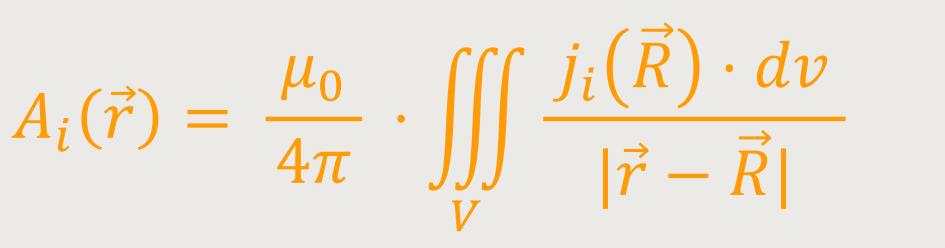
Nun lässt sich das auch vektoriell schreiben:
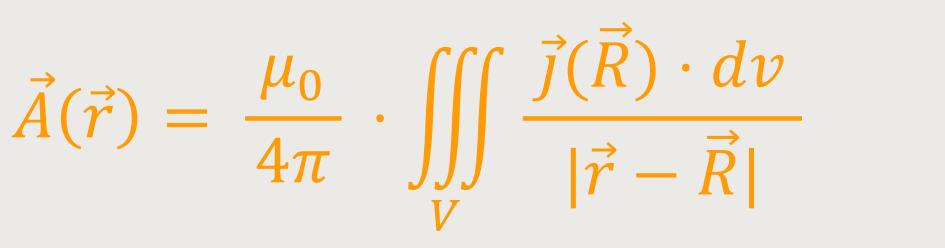
Auf diese Weise erhält man das Vektorpotential für ein Magnetfeld.
Aber jetzt kann man noch einen Schritt weitergehen, weil es ja letztlich um die Rotation geht:
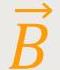 =
rot
=
rot (s.o.)
(s.o.)
Und dann ergibt sich entsprechend für die Rotation:
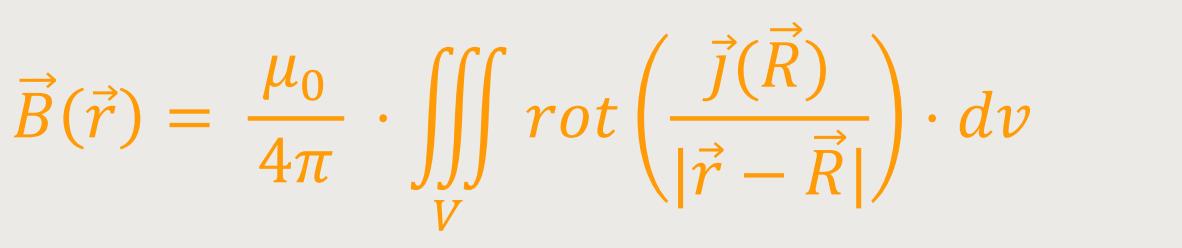
Nach verschiedenen Umformungen kann die Rotation gleichgesetzt werden mit:
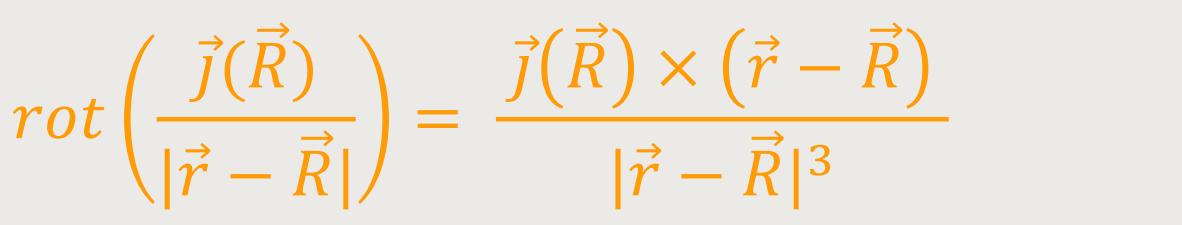
Nach Einsetzen diese Ausdrucks in vorherige Gleichung erhält man unter Berücksichtigung der Stromdichteverteilung in einem dünnen Leiters (Spezialfall) den Ausdruck:
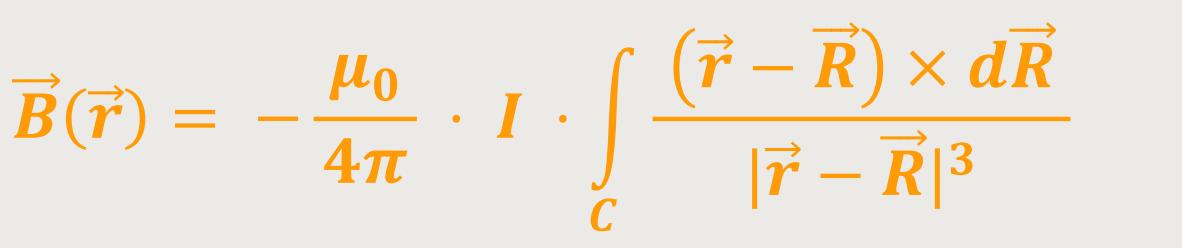
Und das ist das Biot-Savart-Gesetz.
d ist
ein Leiterelement
ist
ein Leiterelement
Hierbei wurde aus der Stromdichte  ein
einzelnes Leiterelement
d
ein
einzelnes Leiterelement
d des
elektrischen Leiters in Stromrichtung.
des
elektrischen Leiters in Stromrichtung.
Welchem Zweck dient obige Vorgehensweise bezüglich der magnetischen Flussdichte, und vor allem wie integriert man jetzt eine solche Gleichung? Diesen Fragen gehen wir im nächsten Kapitel auf den Grund.
⇦ Kapitel Kapitel ⇨