Die Magneto­statik ist ein Themen­gebiet, das zu Beginn seiner Entdeckung zunächst als etwas ganz Separates betrachtet wurde. Man hielt es neben der Gravitations­kraft und der elek­trischen Kraft ledig­lich für eine weitere Kraft, nämlich die magne­tische Kraft. Es war zunächst über­haupt nicht erkennbar, dass es einen unmittel­baren Zusammen­hang zu den anderen Kräften gibt. Denn eine besonders verblüffende Eigen­schaft der Elektro­dynamik ist, dass zwei scheinbar unabhängig vonein­ander wirkende Kräfte sehr eng mitein­ander verbunden sind.

Schließlich erkannte man hinter diesen beiden Kräften eine wechsel­wirkende Kraft, die sinnvoller­weise nur zusammen als die „elektro­magnetische” Wechsel­wirkungs­kraft angesehen werden kann. Diese Erkenntnis ist wie so oft, aus einem Experiment hervor­gegangen. Mit diesem Thema geht eine der ganz großen Vereinheit­lichungen einher.

Die ersten Erfahrungen in der Antike wurden mit minera­lischen Erzen gemacht, die merk­würdige Wechsel­wirkungen hervor­gerufen haben. Diese Erze wurden in der Nähe der Stadt Magnesia gefunden, und hat man deshalb im weiteren Verlauf als „Magnet” bezeichnet. Ähnlich wie der Bernstein als Elektron bezeichnet wurde, und daraus später die Elektrizität formuliert wurde.

Wie bei der Lehre von der Elektri­zität hat man auch bei der Magneto­statik ähnliche Befunde entdeckt. So gibt es zum Beispiel zwei Arten von magne­tischen Polen. Gleich­namige Pole stoßen sich ab, während sich ungleich­namige Pole anziehen. Die Kräfte, die hierbei wirken, sind recht hoch, wobei diese Kräfte auf den Eigen­schaften der Materie selbst beruhen. Hier hat man es mit ferro­magnetischen Werk­stoffen, insbe­sondere mit Eisen, zu tun. Diese gut sicht­baren Auswirkungen sind auf Quanten­effekte zurück­zuführen und haben im Wesent­lichen mit dem Werkstoff zu tun.

Das besondere an den magne­tischen Dipolen ist, dass man diese zu einem größeren Körper zusammen­fügen kann und sie bilden dann ihrer­seits einen größeren Dipol. Wenn man in umge­kehrter Richtung einen Dipol halbiert und diesen in immer kleinere Teil­stücke zerteilt, werden es jedoch immer Dipole bleiben. Es ist nicht möglich, daraus einen Monopol zu kreieren, wie es zum Beispiel bei der elek­trischen Punkt­ladung der Fall ist. Man kann gegen­wärtig keine magne­tischen Monopole abtrennen.

Wie lassen sich die Kraft­wirkungen in der Umgebung von magne­tischen Dipolen charakte­risieren? Zunächst ist es sinn­voll, sich gewisse Indikatoren zu beschaffen. Damit diese entsprechend gut funktio­nieren, müssen sie eben­falls eine ferro­magnetische Eigen­schaft haben. So kann man als Indikator für die Kraft­wirkung in einem Magnet­feld Eisen­feilspäne verwenden. Auch Magnet­nadeln eignen sich gut dafür. Ein optischer Effekt der Eisen­feilspäne ist, dass sich diese entlang der magne­tischen Feld­linien anordnen.

Auch die Erde hat ein magne­tisches Feld, das Erd­magnetfeld. Und dieses Erd­magnetfeld lässt sich eben­falls mit einer Magnet­nadel nach­weisen. Aller­dings spricht man aufgrund der Ausrichtung der Magnet­nadel nicht von einem Plus- und Minuspol, sondern bei einem Magneten ist dann die Rede von einem Nord- und Südpol.

Wenn man für die Bestimmung des Erdmagnet­feldes eine solche Magnet­nadel als Indikator hernimmt, wird die Seite der Magnet­nadel, die zum Norden hinzeigt, als Nordpol bezeichnet. Dabei stellt genau genommen heraus, dass der Magnetpol der Erde ein magne­tischer Südpol ist, weil sich nur ungleiche Pole anziehen. Im Grunde befindet sich der erd­bezogene magne­tische Südpol am geogra­fischen Norden. Da sich aber durch die See­fahrt die Bezeichnung für die Pole der Nadel schon einge­bürgert hatte, tauschte man einfach die Pole der Erde aus. Wo also nun der Norden der Kompass­nadel hinzeigt, befindet sich der magne­tische Südpol der Erde.

Weil man, wie bereits erwähnt, keine magne­tischen Monopole erzeugen kann, gibt es auch keine magne­tische Feld­stärke als Kraft pro Pol­stärke. Aus diesem Grund gibt es nur einen indirekteren Zugang zur Magneto­statik, als wir es von der Elektro­statik her kennen­gelernt haben. Dennoch lässt beides in ein einheit­liches Gesam­tbild eingliedern.

Im Jahre 1820 hat Hans Christian Ørsted entdeckt, das magne­tische und elek­trische Erschei­nungen eng mitein­ander verknüpft sind. So hat er beispiels­weise bei einem seiner Experi­mente einen Strom fließen lassen. Hierbei viel ihm auf, dass sich eine in der Nähe befind­liche Magnet­nadel quer zu einer gerad­linigen Strom­leitung ausrichtete.

Augen­scheinlich stellen sich die magne­tischen Wirkungen rund um diesen gerad­linigen strom­durch­flossenen Leiter so dar, dass sich die Magnet­nadel quer einstellt. Was bedeutet das für das gesamte Magnet­feld um einen solchen Leiter herum?

Offen­sichtlich bildet sich rund um diesen Leiter, in Kreisen ange­ordnet, ein magne­tisches Feld aus. Oder anders ausge­drückt, rund um diesen Leiter gibt es einen „magne­tischen Feld­wirbel”. Und dieser Feld­wirbel sorgt auch dafür, dass sich die Magnet­nadel tangential zu den Feld­linien ausrichtet. Und damit ist der Ausgangs­punkt gegeben, zu einer Vereinheit­lichung der elek­trischen und magne­tischen Phänomene.

Grafik (wird später eingefügt)

Neben dem gerad­linigen Leiter kann man auch eine strom­durch­flossene Spule betrachten. Dort kommt es im Nah­bereich der Spulen­windungen zu magne­tischen Feld­linien, die sich über­lagern und sich außer­halb zu glatten Feld­linien ausbilden. Im Inneren der Spule befindet sich das Magnet­feld, welches in eine Richtung verläuft und sich außen herum wieder schließt. Und so entsteht auch in einer strom­durch­flossenen Magnet­spule ein Magnet­feld, welches einen Dipol­charakter aufweist. Es gibt demnach einen Zusammen­hang zwischen magne­tischen Feldern und elek­trischen Strömen.

Wir werden jetzt zusätz­lich zwei Begriffe einführen, die uns im weiteren Verlauf begleiten werden. Das sind die magnetische Flussdichte und die magnetische Spannung.

Unter der „magne­tischen Fluss­dichte” versteht man im Wesent­lichen ein Vektor­feld . Dieser Vektor charakte­risiert die Wirkungen magne­tischer Felder. Was es im Einzelnen damit auf sich hat, werden wir später noch betrachten.

Für gerad­linige unend­lich lange dünne strom­durch­flossene Leiter gilt, dass der Betrag der magne­tischen Fluss­dichte proportional zum Strom ist. Des Weiteren wird die Wirkung des Feldes vom Abstand abhängig sein. Und ähnlich wie beim Coulomb-Gesetz spielt zusätz­lich ein gewisser Faktor eine Rolle.

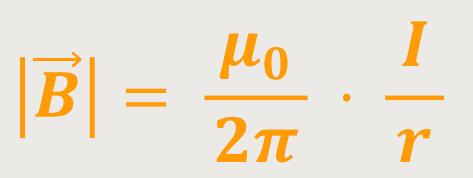
μ₀   ist die magnetische Feldkonstante

Diese magnetische Feld­konstante wird definiert als:

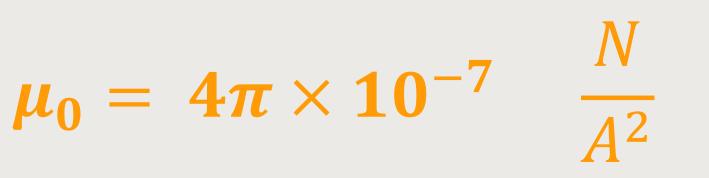
Mit dieser Definition lässt sich bei einer vorgegeben Strom­stärke in einem Leiter das Vektor­feld bestimmen.

Die Dimension der magne­tischen Fluss­dichte ergibt sich jetzt entspre­chend durch Einsetzten:

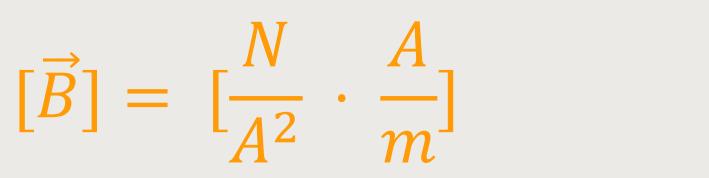
Wenn man mit m erweitert ergibt sich:

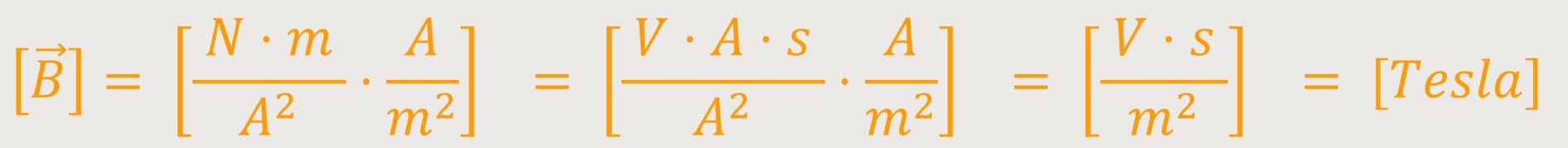
Wenn wir uns erinnern, bei der Elektro­statik wurde der Begriff der dielek­trischen Verschie­bung erwähnt. Die Dimension dieser dielek­trischen Verschie­bung wurde definiert als:

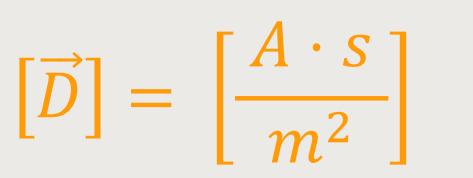
Folglich wird bei dieser Beziehung nur Volt gegen Ampere ausge­tauscht, und man erhält eine formale Analogie zur Fluss­dichte bzw. dielek­trischen Verschiebung.

Eine weitere wichtige Größe ist die „magne­tische Spannung”. Obwohl sie nicht identisch ist mit der elek­trischen Spannung, ist sie dennoch analog definiert:

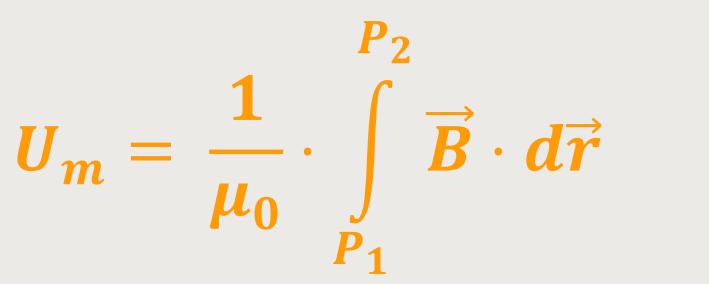
Also, die magne­tische Spannung ist wie die elek­trische Spannung definiert, nur dass man jetzt zusätz­lich den magne­tischen Fluss­dichte­vektor betrachtet. Wobei man aller­dings noch einen konstanten Vorfaktor berück­sichtigt.

Die Dimension dieser elek­trische Spannung wird definiert als:

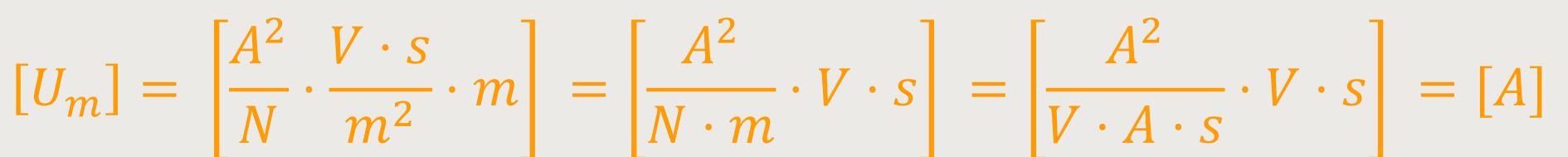
Demnach wird die magnetische Spannung in Ampere gemessen. Wogegen die elektrische Spannung in Volt gemessen wird.

Mit dieser Beziehung lässt sich jetzt die magne­tische Spannung längs eines Kreises bzw. einer geschlossenen Kurve um einen gerad­linigen Leiter bestimmen. Bezogen auf eine geschlossene Kurve K ergibt sich:

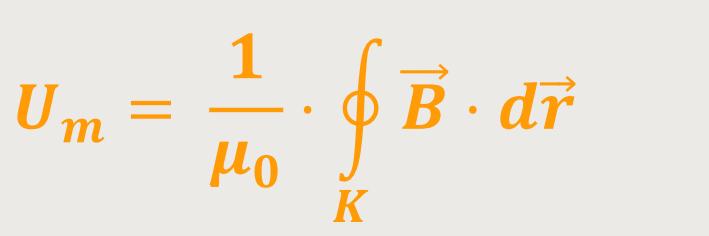
Wenn man das Ringintegral umformt, erhält man:

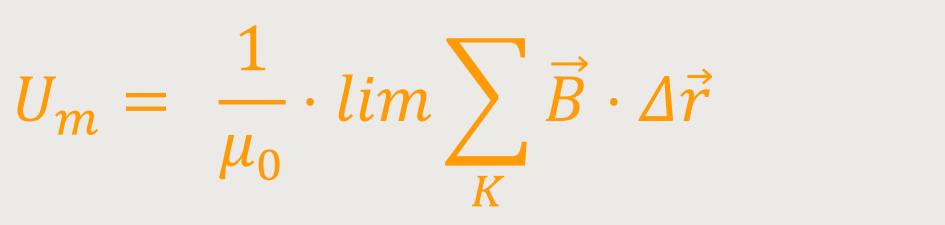
Das entspricht dem Grenz­wert für immer feinere Eintei­lungen als Summe über den ganzen Kreis.

Die magne­tische Fluss­dichte verläuft parallel zu den Teil­stücken und beschreibt den Wirbel rund um diesen Leiter herum. Insofern kann man für den Term auch schreiben:

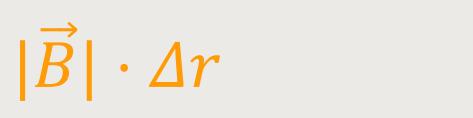
Der Betrag der magne­tischen Fluss­dichte || bleibt in einem bestimmten Abstand R immer gleich. Und da sie konstant bleibt, kann man diese herausheben:

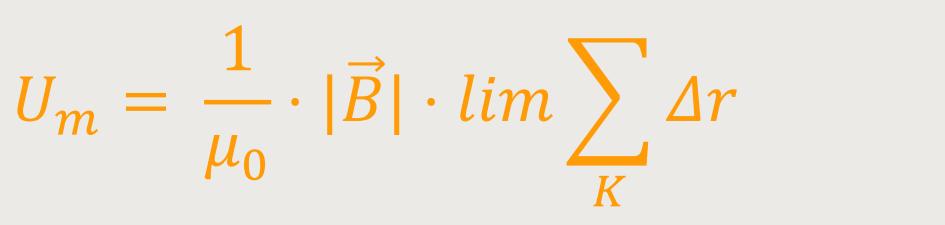
Und da es sich bei der Grenz­wert­betrachtung um einen Kreis handelt, wobei man auch entspre­chend für den Betrag || einsetzt, kann man auch schreiben:

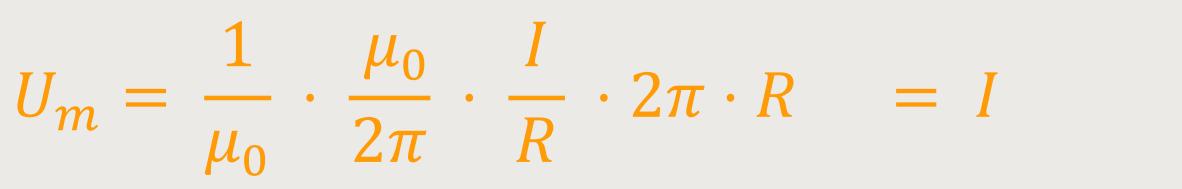
Die magne­tische Spannung längs eines Kreises, rund um den strom­durch­flossenen Leiter, ist gleich dem Strom, der durch diesen Leiter hindurch­fließt.
Und das ist das berühmte Ampere'sche Gesetz:

Das gilt nicht nur für einen konzen­trischen Kreis, sondern für jede beliebige geschlossene Kurve, die einen Strom I umfasst. Das Gesetz sagt also aus, das die magne­tische Spannung längs einer solchen Kurve, durch die ein gewisser Strom hindurch­tritt, gleich dem Strom ist.

Dieses Gesetz ist das Gegen­stück zum Gauß'schen Gesetz in der Elektrostatik.

⇦ Kapitel Kapitel ⇨