Magnetfelder in gerad­linigen strom­durch­flossenen Leitern zu betrachten ist eine Sache. Aber besonders wichtig sind Geometrien in kreis­förmigen Strom­schleifen oder in Form einer Spule.

Spulen bieten sich besonders gut an, um homogene magne­tische Felder hervor­zurufen. Durch derartige Anordnungen wird besonders deutlich, was unter der magne­tischen Fluss­dichte zu verstehen ist.

Ähnlich wie bei zylin­drischen Strom­leitern lässt sich auch die Spule durch Anwen­dung des Ampere'schen Gesetzes beschreiben.

Bei einer Spule handelt es sich im Grunde um eine schrauben­förmige Aufwicklung eines dünnen Leiters.

n   ist die Anzahl der Windungen pro Längeneinheit
L   ist die Länge der Spule
N   ist die Gesamtwindungszahl der Spule

Der Radius kann bei der Ermittlung der magne­tischen Fluss­dichte vernach­lässigt werden. Aller­dings ist in diesem Fall der Durch­messer im Verhältnis zur Länge sehr klein.

Grafik (wird später eingefügt)

Eine solche Spule zeichnet sich dadurch aus, dass der Außen­raum prak­tisch feld­frei ist und der Innen­raum einem nahezu homogenen Feld entspricht.

Um die magne­tische Fluss­dichte auszu­rechnen, betrachtet man einen recht­eckigen Verlauf, dessen eine lange Seite identisch ist mit der Mittel­achse der Spule, dann am Ende quer abzweigt, und außer­halb der Spule wieder zurück­läuft. Die Eck­punkte des Recht­ecks werden mit A−B−C−D bezeichnet.

Man geht deshalb so vor, um zunächst einmal die magne­tische Spannung längs dieses geschlossenen Weges zu ermitteln. Die Grund­gleichung für die magne­tische Spannung lautet ja:

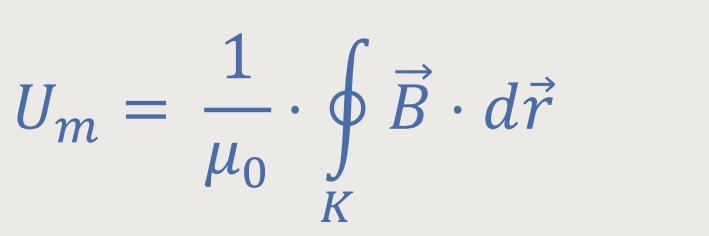
Auch in unserem Fall ist das Innen­feld weitest­gehend homogen und der Außen­raum feld­frei. Des Weiteren herrscht nur im Inneren der Spule eine Fluss­dichte vor, die zudem über die gesamte Länge L konstant ist. Die anderen drei Teil­stücke des Rechtecks liefern keine Beträge. Insofern reduziert sich das Integral zu einer einfachen Gleichung:

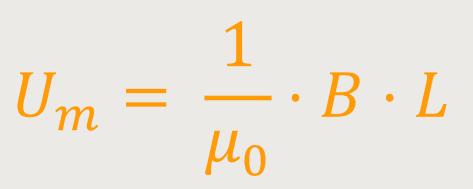
Nun besagt das Ampere'sche Gesetz, dass die magne­tische Spannung gleich dem von dem Weg umschlossenen Strom ist. Wie muss man sich jetzt diesen Weg konkret vorstellen? Das Recht­eck gleicht einer aufge­spannten Fläche, welche die Spulen­länge umschließt. Jede dieser Spulen­windungen durch­stößt diese Fläche. Der Strom I fließt also n-mal durch die Gesamt­windungs­zahl N = n · L hindurch. Somit ergibt sich für die magne­tische Spannung:

Und der Betrag für die magne­tische Fluss­dichte ist dann:

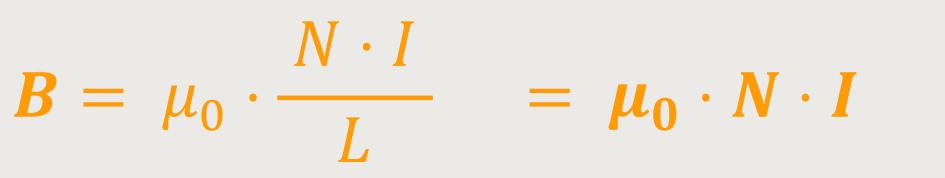
Diese Über­legung ist jedoch nur dann erfüllt, wenn der Spulen­durch­messer sehr klein ist gegen­über der Länge der Spule.

Natürlich könnte man auch eine Spiegelung in ein Links­basis­vektor­system vornehmen. Dann müssten aller­dings die Basis­vektoren in ein Links­system trans­formiert werden.

Grafik (wird später eingefügt)

In einem rechts­sinnigen Koordinaten­system fließt der Strom gemäß der Rechte-Hand-Regel. Das Magnet­feld verläuft im Strom­leiter entspre­chend dieser Regel rechts­läufig, sodass die magne­tische Fluss­dichte inner­halb der Spule auch nur in eine Richtung verläuft.

Bei der kreis­förmigen Strom­schleife betrachtet man im Grunde auch eine Spule, aber nur mit einer Windung. Man kann hier auch von einem Kreis­strom sprechen. Auf der Strom­schleife liegen wieder die einzelnen Strom­elemente d. In der Mitte der Strom­schleife verläuft senk­recht die z-Achse und im Zentrum liegt der Ursprung. Etwas entfernt vom Ursprung sitzt der Beobachter auf der z-Achse im Aufpunkt P. Der Orts­vektor wird mit bezeichnet. Dann ist der Orts­vektor des Leiter­elements. Der Verbindungs­vektor vom Aufpunkt zum Leiter­element ist wie so oft − . Wir hatten eine ähnliche Beschreibung im vorherigen Kapitel.

R   ist der Radius der Schleife

Grafik (wird später eingefügt)

Vom Biot-Savart-Gesetz wissen wir, dass:

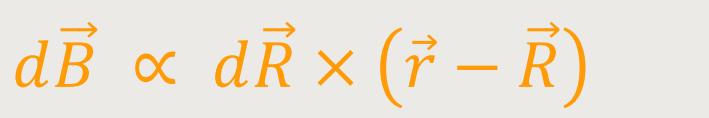
Und wenn man das aufinte­griert, erhält man:

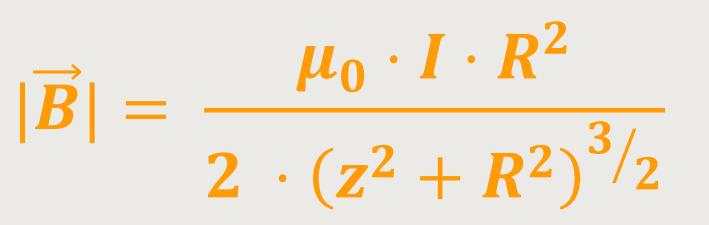
Für den Schleifen­mittel­punkt bedeutet das, wenn der Aufpunkt im Ursprung liegt und damit z = 0 setzt:

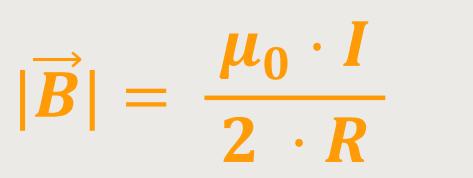
Auch hier haben wir wieder bei dem Feld eine Abhängig­keit von 1 /R.

Der Feldverlauf lässt sich grafisch darstellen:

Grafik (wird später eingefügt)

Grafik (wird später eingefügt)

Das Modell der strom­durch­flossenen Leiter­schleife verwendet man auch, um das magne­tische Dipolmoment zu definieren:

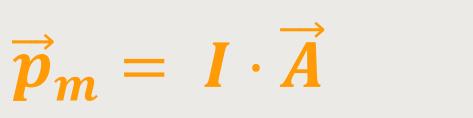
Grafik (wird später eingefügt)

Hierzu kann man sich eine strom­durch­flossene Strom­schleife denken, die eine Fläche A umschließt, mit einem senk­recht dazu angeordneten Flächen­vektor . Die Länge des Flächen­vektors entspricht der Fläche. Das magne­tische Dipol­moment verläuft parallel zum Flächen­vektor. Und das Dipol­moment als Vektor ist gleich dem Strom in dieser Leiter­schleife, multi­pliziert mit dem Flächen­vektor der kreis­förmigen Fläche, die von der Leiter­schleife umschlossen wird.

Für diese Betrach­tung wird der Bezugs­punkt P jetzt auf der z-Achse weit weg gelegt. Dann ist z ≫ R, und wird deshalb auch als Fern­feld bezeichnet.

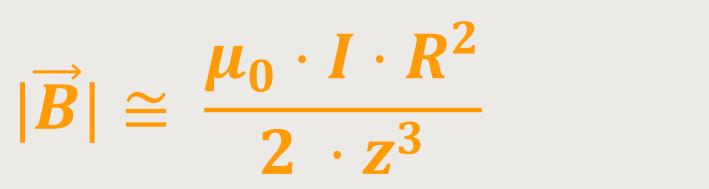
Um die Schleifen­fläche mit zu berück­sichtigen, erweitert man die Gleichung mit π (Pi), und dann erhält man:

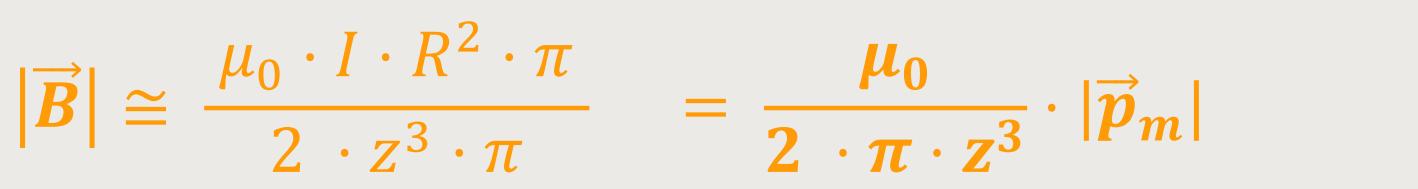
Wenn das magne­tische Feld weit weg ist vom Dipol, lässt sich das Feld beschreiben, als propor­tional zum magne­tischen Dipol­moment und propor­tional zu 1 /z³. Das ist vergleich­bar mit dem elek­trischen Dipol. Während das Feld bei der Punkt­ladung mit 1 /r² zurück­geht, geht beim elek­trischen Dipol das elek­trische Feld mit 1 /r³ zurück.

Da es aber bei den magne­tischen Phäno­menen keine magne­tischen Punkt­pole bzw. Mono­pole gibt, geht das magne­tische Fern­feld daher mit 1 /z³ zurück. Und das ist analog zum elek­trischen Dipolfeld.

Nun stellt sich die Frage, was passiert denn über­haupt in einem magne­tischen Feld?

Auf ruhende elek­trische Ladungen wird in einem Magnet­feld keine Kraft ausgeübt. Bewegte Ladungen dagegen, also elek­trische Ströme, umgeben sich mit Magnet­feldern.

Was passiert also, wenn ein solcher Strom durch ein Magnet­feld fließt?

Das Feld bewirkt eine Kraft­wirkung auf einen strom­durch­flossenen Leiter. Diese Kraft­wirkung wird auch als die Lorentz­kraft bezeichnet. Die Kraft wirkt ⊥ auf die Strom­richtung und ⊥ auf das Vektor­feld .

Und wenn man diese Abhängig­keit bei dem Ampere'schen-Gesetz berück­sichtigt, ergibt sich:

Grafik (wird später eingefügt)

Anderer­seits kann man sich auch einen strom­durch­flossenen Elektro­lyten in einem Magnet­feld vorstellen. Hierbei ist in einem flachen Gefäß mit Flüssig­keit im Zentrum ein Permanent­magnet ange­ordnet. Die Magnet­felder verlaufen in verti­kaler Richtung durch den Elektro­lyten, indem sie in die Flüssig­keit eintauchen und wieder austreten. Am Innen­rand des Gefäßes und am Außen­umfang des Magneten verlaufen jeweils die Elektroden.

Sobald eine Spannung angelegt ist, werden die Ionen radial nach außen wandern, und damit einen Strom­fluss erzeugen. Daraus ergibt sich die Strom­richtung sowie die Feld­richtung, und senk­recht zu beiden die Kraft­wirkung. Das bedeutet, dass Ionen durch diese Kraft­wirkung seitlich abge­lenkt werden. Dabei entsteht eine Reibung zwischen den Ionen und der Elektrolyt­flüssig­keit. Als Ergebnis lässt sich eine hydro­dynamische Wirbel­strömung beobachten.

Die Kraftwirkung auf Ströme lässt sich wie folgt darstellen:

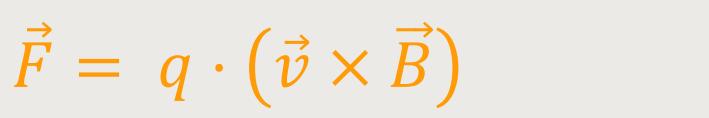
  ist die Geschwindigkeit der Ladungsträger

Wenn man einen Ladungs­träger mit Ladung q und der Geschwindigkeit durch das magne­tische Feld hindurch­schickt, wird sich die Kraft ergeben. Damit erhält man eine konkrete Inter­pretation der magne­tischen Fluss­dichte.

Analog dazu hatten wir bereits die Kraft­wirkung aus der Elektro­dynamik kennen gelernt:

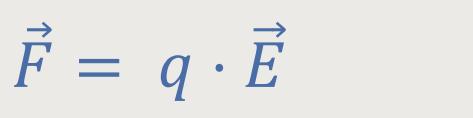
Denn die elek­trische Feld­stärke war die Kraft pro Ladungs­einheit.

Beim Magnet­feld kommt es zusätz­lich auf die Geschwindig­keit an. Und wenn diese Null ist, dann gibt es auch keine Kraft­wirkung. Damit ergibt sich in einem elektro­magnetischen Feld, eine Gesamt­kraft aus beiden Einzel­kräften:

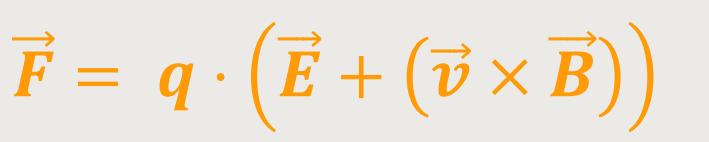
Das ist die Definition der Lorentzkraft.

Während die Maxwell-Gleichungen es nur erlauben, aus Ladungen und/oder Strömen die Felder zu ermitteln, ergibt sich bei bekannten Feldern jetzt eine Kraft­wirkung auf bewegte Ladungen in diesen Feldern. Insofern sind die Felder zwischen­geschaltet, einer­seits zwischen den feld­erzeugenden Ladungen und ander­seits den bewegten Ladungen und Strömen, auf die diese Kraft ausgeübt wird.

Insgesamt erlauben die vier Maxwell-Gleichungen zusammen mit der Lorentz­kraft die Berechnung der Kraft­wirkung in elektro­magnetischen Feldern. Und alles zusammen beschreibt die elektro­magnetische Wechsel­wirkung.

⇦ Kapitel Kapitel ⇨