Im vorherigen Kapitel haben wir das Biot-Savart-Gesetz hergeleitet.

Dieses Gesetz beinhaltet eine wichtige Gleichung zur Berechnung von Magnet­feldern. Ein solches Magnet­feld entsteht immer auf­grund eines fließenden Stroms. Es wurde wie folgt definiert:

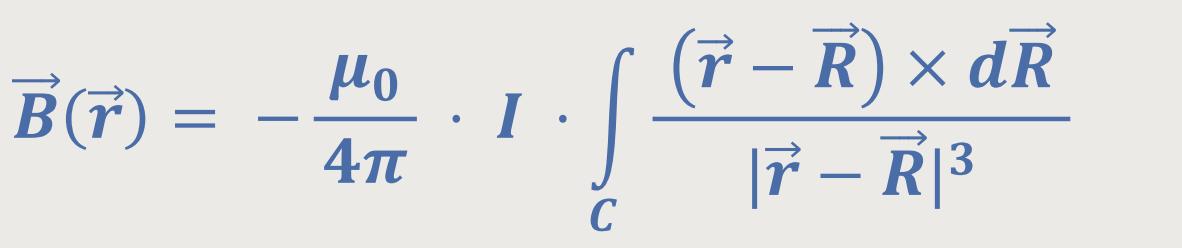
Jetzt stellt sich die Frage, wie man dieses Gesetz konkret anwenden kann. Dazu ist es von Vorteil, sich noch­mals zu verdeut­lichen, was es bedeutet. Zunächst einmal geht es um die magne­tische Fluss­dichte in einem Raum, von einem Beobachtungs­punkt aus betrachtet.

Neben einer voran­gestellten Konstante spielt immer der jeweils fließende Strom eine wichtige Rolle. Darüber hinaus folgt eine mathe­matische Inte­gration über ein Linien­element d des Leiters in Strom­richtung. Bei einem solchen Linien­integral über eine Kurve C inte­griert man über die ganzen Elemente des jeweiligen Strom­leiters.

Die magne­tische Fluss­dichte eines einzelnen Strom­elements stellt sich betrags­mäßig wie folgt dar:

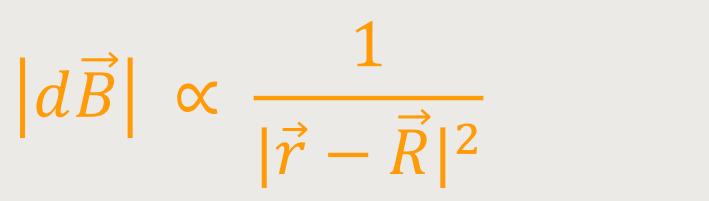
Damit ergibt sich eine Abhängig­keit analog zu den elek­trischen Punkt­ladungen. So vorzu­gehen macht Sinn, weil man ja auch nur ein einziges Strom­element betrachtet, welches umgeben ist von einem magne­tischen Feld. Verständlicher­weise gibt es natürlich nicht nur ein solches Strom­element.

Grafik (wird später eingefügt)

Dazu könnte man sich einen langen dünnen strom­durch­flossenen Leiter vorstellen. Von Interesse ist nun das Magnet­feld um einen derartigen Leiter herum. Ausgehend von einem will­kürlichen fest­gelegten Ursprung des Koordinaten­systems betrachtet man jetzt ein einzelnes Leiter- bzw. Strom­element d. Der Vektor ist dann der Orts­vektor vom Ursprung zum jeweiligen Strom­element. Der Beobachter befindet sich irgendwo an einem Aufpunkt P, dessen Orts­vektor ausgehend vom Ursprung mit beschrieben wird. Im Wesent­lichen inter­essiert uns aber die magne­tische Fluss­dichte , mit dem sich der ganze Strom­leiter umgibt, an der Stelle des Beobachters. Zunächst geht es nur um das Magnet­feld eines Strom­elements aus dem Leiter. Insofern gibt es noch einen weiteren Verbindungs­vektor von diesem Strom­element zum Aufpunkt P des Beobachters. Der wird durch den Vektor − beschrieben. Daher ergibt sich sofort aus dem Biot-Savart-Gesetz die Fluss­dichte für ein einzelnes Stromelement:

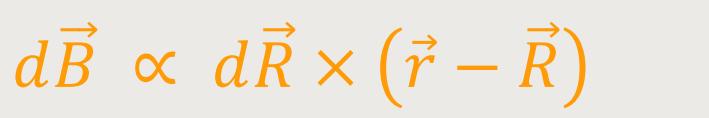
Auf diese Weise erhält man die Richtung und auch den Orientierungs­sinn des Vektors der magne­tischen Fluss­dichte d. Für eine komplette Unter­suchung muss man lediglich über alle Leiter­elemente summieren bzw. integrieren.

Bei einem solchen Vektor­produkt gilt es zu beachten, welches Basis­vektor­system man wählt. In diesem Fall geht es um ein Rechts­system. Damit erhält man für die Orien­tierung des Magnet­feld­wirbels eine Rechts­schraubenregel in Richtung des fließenden Stroms.

Natürlich könnte man auch eine Spiege­lung in ein Links­basis­vektor­system vornehmen. Dann müssten aller­dings die Basis­vektoren in ein Links­system transformiert werden.

Die einfachste Geometrie ist ein gerad­liniger zylin­drischer Strom­leiter. In der Elektro­statik greift man dafür oft auf das Gauß'sche-Gesetz zurück. Bei den Magnet­feldern dagegen über­nimmt diese Rolle das Ampere'sche-Gesetz. Bei zylin­drischen Strom­leitern, reicht es aus, auf dieses Ampere'sche-Gesetz zurück­zugreifen.

Da wir vorerst bei einer zylin­drischen Geometrie des Leiters bleiben und es um sehr dünne strom­durch­flossene Leiter geht, werden wir nach­folgend zwei Berech­nungen durch­führen. Einmal mittels Ampere'schen-Gesetz und im Anschluss das Ganze nochmal aus Sicht des Biot-Savart-Gesetzes anwenden.

Das „Ampere'sche-Gesetz” besagte folgendes über die magne­tische Spannung:

Im ersten Schritt geht es um den Außen­raum mit dem Radius r in Bezug auf einen zylin­drischen Leiter mit dem Radius r_₀. Der Außen­raum ist größer als der Leiter­radius r ≥ r_₀.

Grafik (wird später eingefügt)

Im Grunde betrachtet man einen konzen­trischen Kreis K, der den Stromleiter umfasst.

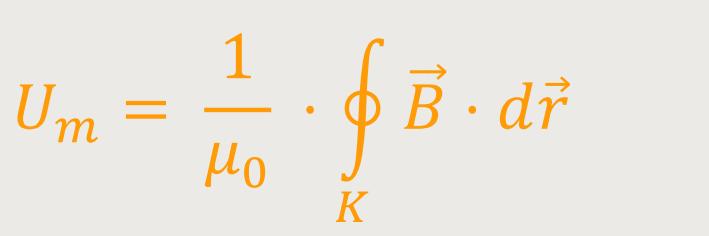
Weil sich der Radius r dieses Kreises nicht ändert, haben die Fluss­dichte­vektoren überall den gleichen Betrag, und deshalb kann man nach vorheriger Umformung auch schreiben:

Wenn man diese Beziehung in das Ampere'sche-Gesetz einsetzt, ergibt sich:

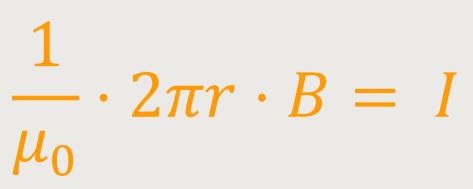
Somit folgt nach Umstellung der Gleichung:

Und damit wird eine frühere Ausgangs­beziehung über die magne­tische Fluss­dichte bestätigt.

Im zweiten Schritt geht es jetzt um den Innen­raum dieses zylin­drischen Leiters r ≤ r_₀. Jetzt betrachten wir einen konzen­trischen Kreis K, der im Inneren des Strom­leiters liegt. Die Ausgangs­gleichung ist wieder die gleiche:

Dieser Forma­lismus ist analog zum Außen­kreis. Der wesent­liche Unter­schied besteht jetzt aller­dings darin, dass der vom Innen­kreis umschlossene Strom nicht mehr dem ganzen Strom in dem Leiter entspricht. Bei einer homogenen Strom­verteilung ergibt sich daher für diesen Strom:

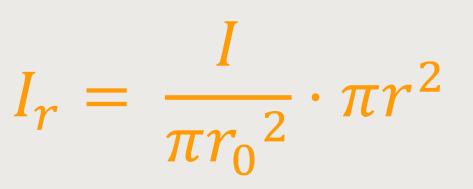
Die Stromdichte, also der Strom pro Quer­schnitts­flächen­einheit, wird multi­pliziert mit der Innen­kreis­fläche. Nach Wegkürzen ergibt sich:

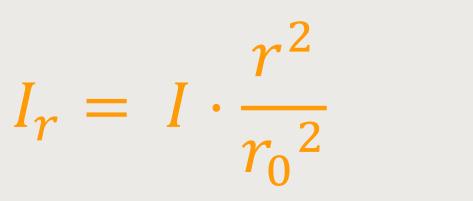
Und wenn man das wieder in das Ampere'sche-Gesetz einsetzt, ergibt sich:

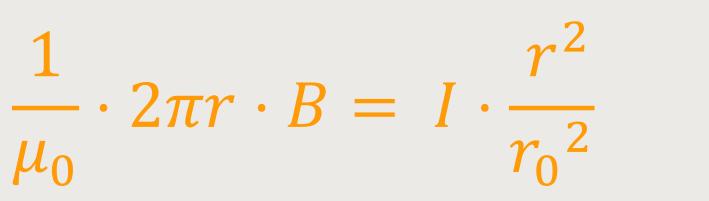
Somit folgt nach Umstellung der Gleichung:

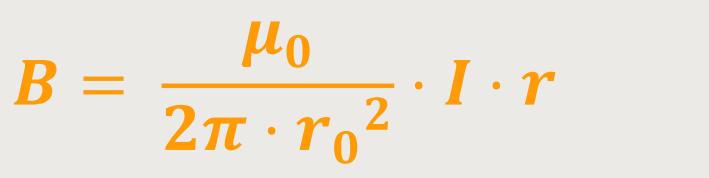
In diesem Fall nimmt die magnetische Fluss­dichte mit dem Radius zu. Denn je größer der Radius r ist, desto größer wird auch der umschlossene Strom.

Grafik (wird später eingefügt)

Im Inneren des Leiters nimmt die Fluss­dichte vom Zentrum bis zur Ober­fläche des Leiters zu, um anschlie­ßend propor­tional mit 1 /r zurück­zugehen. Das Ampere'sche-Gesetz bezieht sich immer auf den Strom, der stets von der entspre­chenden umlau­fenden Kurve einge­schlossen wird.

Jetzt wollen wir das Ganze noch­mals mit Hilfe des „Biot-Savart-Gesetzes” durch­rechnen. Hierzu betrachten wir wieder einen dünnen gerad­linigen Stromleiter.

Grafik (wird später eingefügt)

Wir denken uns einen solchen Strom­leiter, dessen Strom­fluss in einer senk­rechten Richtung von unten nach oben verläuft. Die Mittel­achse bezeichnen wir daher als z-Achse.

Der Beobachter befindet sich irgendwo rechts außer­halb des Leiters in einem Aufpunkt P. Dann legen wir einen Fußpunkt auf der Senk­rech­ten fest, indem wir vom Beobachtungs­punkt eine lotrechte Verbin­dungs­linie ziehen. Jetzt liegt der Ursprung O genau auf dem Strom­leiter. Im Anschluss betrachten wir ein kleines Strom­element d an irgend­einer Stelle des Leiters. Die Position wird vom Ursprung beschrieben durch den Vektor . Eine weitere Verbindungs­linie vom Ursprung zum Aufpunkt bildet den Vektor . Ein dritter Vektor − zeigt von der Position des Strom­elements zum Aufpunkt P. Als Ergebnis erhält man ein recht­winkliges Vektor-Dreieck. Diese Vorgehens­weise gleicht vom Grund­satz her der weiter oben Besprochenen. Daraus ergibt sich eine Entsprechung oder Gleich­setzung für die Beträge:

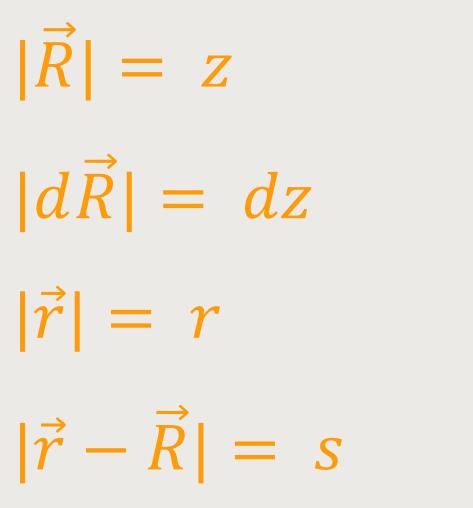
Der eingeschlossene Winkel am Aufpunkt wir mit α bezeichnet. Nun müssen noch alle kleinen Strom­elemente d von − ∞ bis + ∞ aufintegriert werden. Außerdem soll dieser Winkel von − π/2 über Null bis + π/2 variieren. Alle kleinen Strom­elemente zeigen in Richtung der z-Achse.

Für die weitere Betrach­tung nehmen wir, wie gesagt, obiges Biot-Savart-Gesetz hinzu. Die Fluss­dichte­vektoren zeigen im Aufpunkt nach der Rechte-Hand-Regel quasi nach hinten. Und wenn es jetzt um den gesamten Betrag der Fluss­dichte­vektoren geht, müssen abschließend die Beträge von allen d aufsummiert werden, weil sie alle in die gleiche Richtung zeigen.

Wenn man jetzt in das Biot-Savart-Gesetz einsetzt, wobei die Paramater entspre­chend ersetzt werden und anschlie­ßend über die z-Achse integriert wird, ergibt sich:

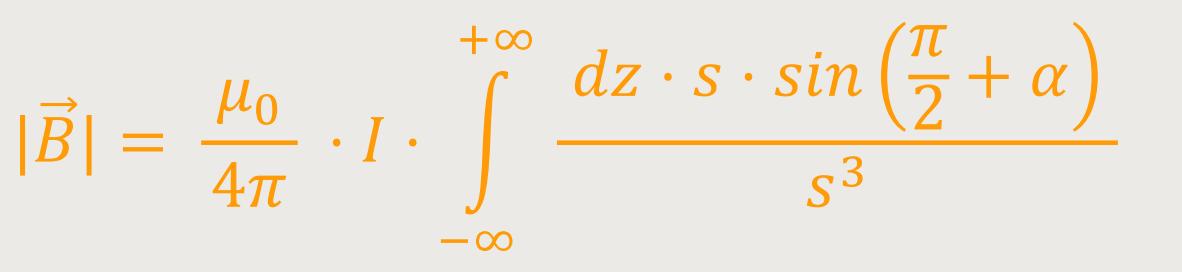
Für den Betrag des Vektors | −| im Vektor­dreieck erhält man:

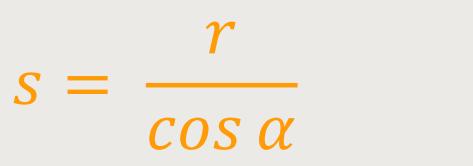
Für die anderen Parameter gilt entsprechend:

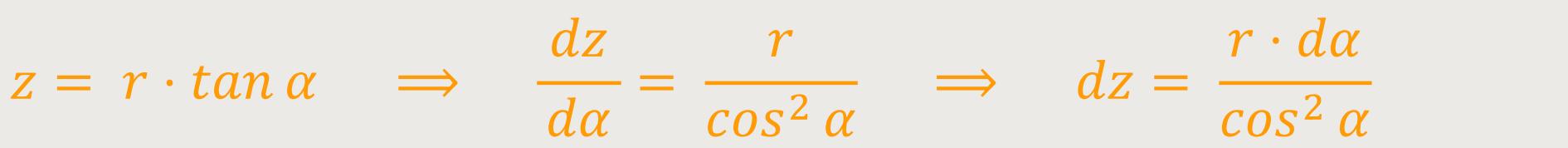
Wenn man jetzt wieder entspre­chend einsetzt, ergibt sich:

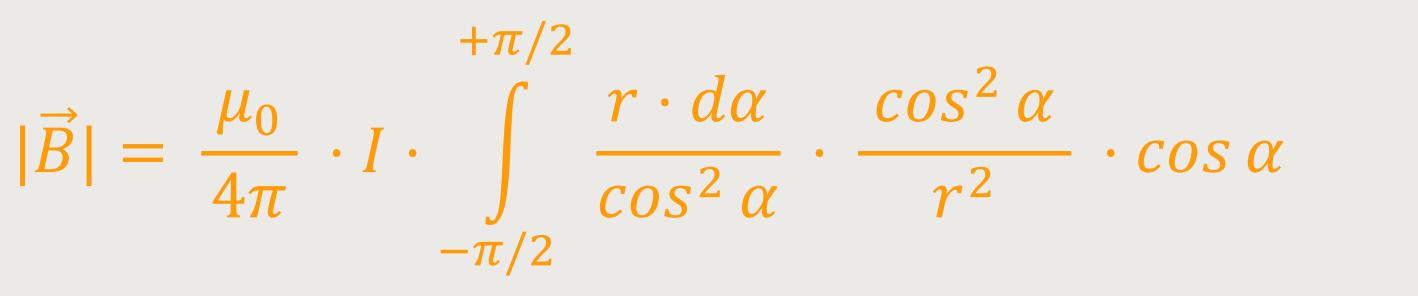
Da der Radius r eine Konstante ist, lässt sie sich vor das Integral setzen. Und nach dem Wegkürzen, sowie unter Berück­sichtigung, dass rot const ebenfalls Null ist, erhält man:

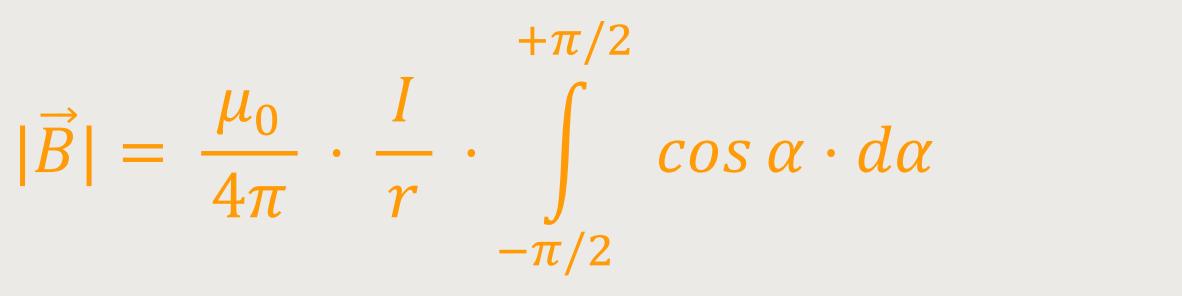
Daraus folgt abschließend:

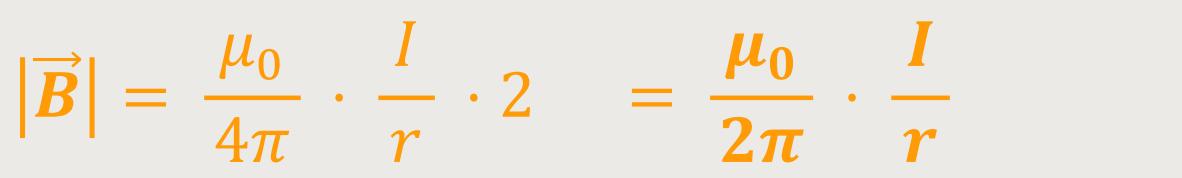
Auf diese Weise lassen sich durch Anwendung des Biot-Savart-Gesetzes die Felder konkret ausrechnen. Beim Inte­grieren ergibt sich aus der ursprüng­lichen 1/r³ Abhängig­keit wieder eine 1/r Abhängig­keit. Insofern bleibt bei dieser Betrach­tung der Innen­raum außen vor, weil es sich um einen dünnen geraden Strom­leiter handelt.

⇦ Kapitel Kapitel ⇨