Weil alle Kräfte zum Kraft­zentrum, nämlich der Sonne, hinge­richtet sind, ist das äußere Dreh­moment = 0. Daher ergibt sich für die Drehimpuls­erhaltung: = const.

Deswegen bleiben die Planeten im Wesent­lichen immer in einer Bahnebene.

Wenn die Erde für einen bestimmten Zeitraum Δt die Sonne umkreist, dann über­streicht der Orts­vektor eine Fläche ΔA. Die Geschwindig­keit als Verschie­bung pro Zeit­einheit ist . Die Fläche, die dabei über­strichen wird, kann man wie folgt ausrechnen:

Als Ergebnis erhält man 1/2 mal den Betrag des vektoriellen Pro­duktes vom Orts­vektor × der Geschwindig­keits­verschiebung · Δt . Es entspricht also der halben Fläche des Vektor-Parallelogramms.

Das lässt sich entsprechend noch umformen, wobei jetzt m die Masse der Erde ist:

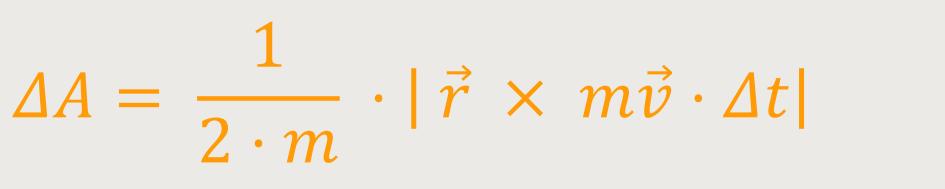
Die Verschiebung der Masse m ist aber der Impuls p. Wenn man das nochmals umformt erhält man:

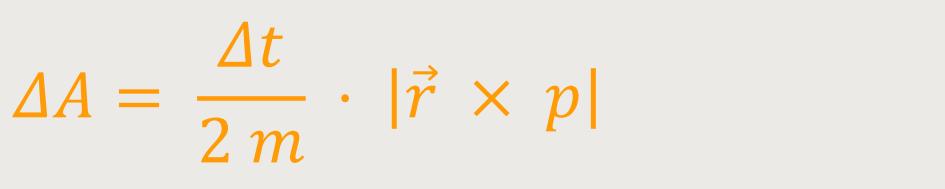
Dieses × p ist nun aber definitionsgemäß der Dreh­impuls . In diesem Fall ist der Dreh­impuls = const . Damit ergibt sich, wobei man das Ganze immer in gleichen Zeit­intervallen betrachtet, und bei gleich­bleibender Masse der Erde, dass eben­falls die Fläche ΔA = const ist. Und das ist bereits eines der „Keplerschen Gesetze”.

Die Planeten­bahnen verlaufen so, dass in gleichen Zeit­intervallen jeweils vom Radius­vektor gleiche Flächen über­strichen (oder über­schritten) werden.

Hierbei muss man also noch nicht einmal die konkrete detail­lierte Wechsel­wirkungs­kraft berück­sichtigen. Man muss bei obiger Betrachtung auch nicht das Newtonsches Gravitations­gesetz anwenden. Es reicht bereits aus, von einer Zentralkraft auszugehen, und das der Dreh­impuls eine erhaltene Größe ist. Und daraus folgt bereits das 2. Keplersches Gesetz.

Der Radius­vektor über­streicht in gleichen Zeiten gleiche Flächen.

Das lässt sich auch durch den Drehimpulssatz begründen, den wir bereits in einem früheren Kapitel betrachtet haben. Unter Verwen­dung des Gravitations­gesetzes kann man des Weiteren zeigen, dass noch zwei weitere Gesetze bestehen.

Das eine hat mit dem 1. Keplerschen Gesetz (Fortsetzung) zu tun:

Die Planeten­bahnen sind Ellipsen, in deren einem Brenn­punkt die Sonne steht. Der eine Brenn­punkt ist nicht genau die Sonne, sondern der gemeinsame Schwer­punkt von Sonne und Planet.

Dieses Gesetz der „Ellipsen­bewegung”, bei dem der eine Brenn­punkt die Sonne ist, lässt sich nur unter Verwendung des Newtonschen Gravitationsgesetzes ableiten.

Und ein weiteres wichtiges Gesetz ist das 3. Keplersches Gesetz.

Dieses Gesetz macht eine Aussage über die Umlauf­zeiten und die Halb­achsen, also die großen Bahn­achsen zweier Planeten.

Für zwei Planeten gilt, wenn sie nicht unter­einander in Wechsel­wirkung sind:

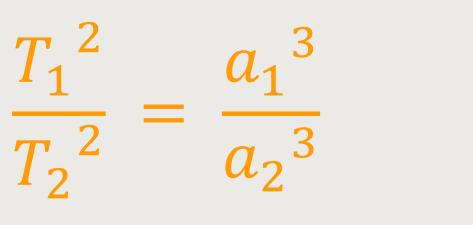
a   ist die große Halb­achse (Bahnachse) der Bahn­ellipse (Planeten­bahn)
T   ist die Umlaufzeit des Planeten.

Diese experimen­tellen empirischen Befunde von Kepler konnte man später durch Annahme des Gravitations­gesetzes herleiten. Durch die Newtonsche Mechanik konnte man alle scheinbar nicht zusammen­hängenden Gesetz­mäßig­keiten auf nur ein dahinter­liegendes Gesetz zurück­führen.

Aller­dings ist das Gesetz noch nicht ganz stimmig, denn bei Merkur kann man eine relativ starke Bahn­exzentrik beobachten. Die große Bahn­achse bewegt sich im Laufe der Zeit gering­fügig. Der Merkur spiralt quasi auf seiner Umlauf­bahn. Das sind zwar nur ein paar Winkel­sekunden pro Jahrhundert, aber immerhin. Um das zu begründen, braucht es die Allgemeine Relativitäts­mechanik.

Diese Keplerschen Gesetze sind ein wesent­liches Kriterium dafür, dass man das Gravitations­gesetz gegen­wärtig noch als gültig ansieht.

⇦ Kapitel Kapitel ⇨