Das Pendel ist ein schwingungs­fähiges System, das im Wesent­lichen nur aus einem Massen­punkt besteht. Diese Masse ist weitest­gehend an einem masse­losen Faden aufgehängt. Der Faden hat eine gewisse Länge s. Und das Ganze befindet sich in einem homogenen Gravitations­feld auf der Erde. Mit Hilfe der Pendel­bewegung kann man Rück­schlüsse auf das Verhalten der trägen und der schweren Masse ziehen.

Mit der Bewegungs­gleichung lässt sich die Pendel­schwingung beschreiben:

Grafik (wird später eingefügt)

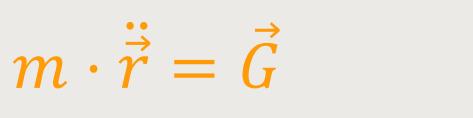
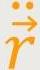  ist die ...
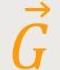  ist die Gewichtskraft

Der Weg ist definiert als:

Die Tangential­komponente des Pendels lautet:

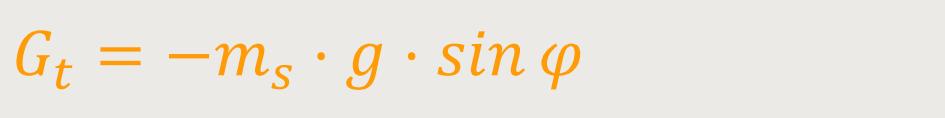
Wenn man sehr kleine Schwingungen betrachtet, kann man auch schreiben:

Damit erhält man die Bewegungs­gleichung für das Pendel:

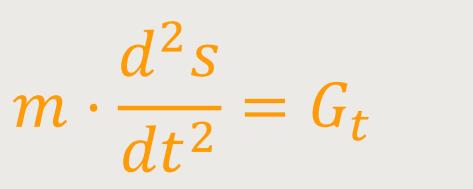
Nach Einsetzten in die Gleichung erhält man folgende Beziehung:

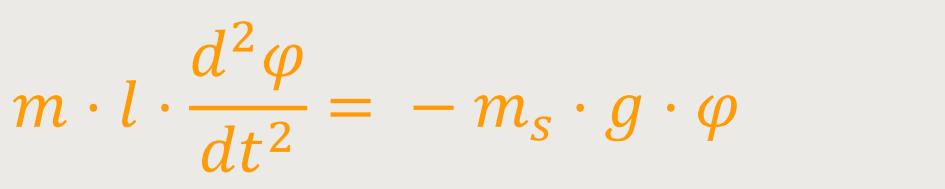
Damit ergibt sich eine Differential­gleichung für die Zeitabhängigkeit des Winkels φ.

Hinweis: In der Physik werden Winkel immer im Bogen­maß ange­geben! Ein rechter Winkel ent­spricht π /2.

Wenn in einer Gleichung die zweite Ableitung ent­halten ist, und die Funktion selbst, dann lässt das einen perio­dischen Zusammen­hang zwischen der Schwingung und der Zeit erkennen.

Daher lässt die Gleichung erahnen, dass es sich um eine harmo­nische Schwingung handelt. Differential­gleichungen lassen sich des ent­weder durch aus­probieren lösen. Aber in der Realität spricht man eher von einem Lösungs­ansatz.

Weil es sich um eine periodische Schwingung handelt, wählt man hier als Lösungsansatz:

A   ist die Amplitude

Um die zweite Ableitung zu erhalten, bildet man zunächst:

Und jetzt gilt für die zweite Ableitung:

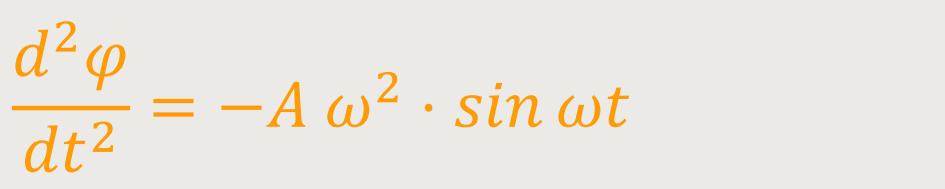
Beide Abhängig­keiten nach der Zeit sind von der Form sin ωt.

Wenn man das jetzt entsprechend einsetzt, erhält man:

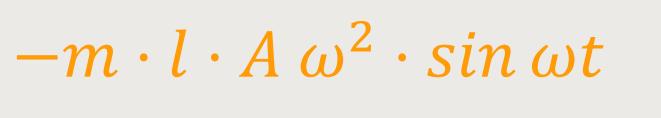
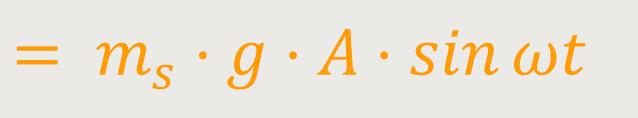
m   ist die träge Masse
l    ist die Pendellänge
A   ist die Amplitude

Nach Wegkürzen erhält man:

Das Pendel wird gleich schnell schwingen, egal ob man die Amplitude größer oder kleiner macht. Hier haben wir aller­dings voraus­gesetzt, dass φ klein ist.

Der Schwingungs­winkel ist demnach:

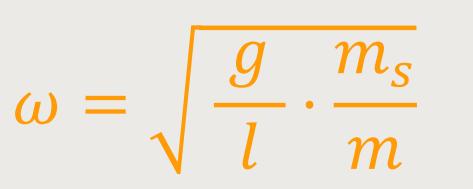
Was lässt über das Verhalten des Sinus sagen? Wenn man zum Beispiel beim Sinus mit dem Argument 0 anfängt, dann ist der sin = 0. Wie viel muss hinzu­gefügt werden, um wieder in die gleiche Situation zu kommen? Das ist 2 · π, nämlich der volle Winkel im Bogenmaß.

Das heißt, die Schwingungs­dauer T wird wie folgt charakterisiert:

Man nennt den Parameter ω auch die „Kreisfrequenz”.

Wenn man entsprechend einsetzt, ist die Schwingungs­dauer demnach:

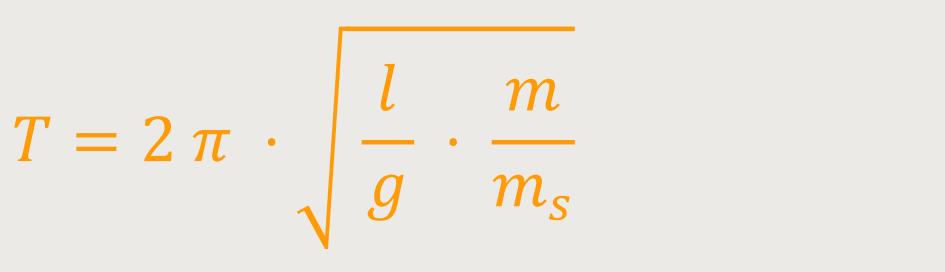
Das kann man nochmals umformen, um einen Zusammen­hang zwischen der schweren und trägen der Masse herzuleiten.

Demnach gilt für die schwere Masse:

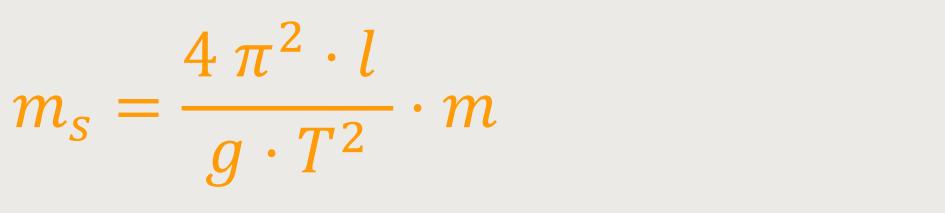
Es stellt sich heraus, dass die schwere Masse m_s propor­tional ist zur trägen Masse m.

Damit wird das Äquivalenz­prinzip bestätigt. Das heißt, die träge und schwere Masse sind äquivalente Größen, die letztlich gleichartig erscheinen und eine gleichartige Eigenschaft der entsprechenden Körper darstellen.

Somit legt man ein für alle Mal fest:
Der Faktor ist 1 und m = m_s.

Demnach hat die Masse auf die Schwingungsdauer keinen Einfluss, und man kann die Gleichung nochmals vereinfachen:

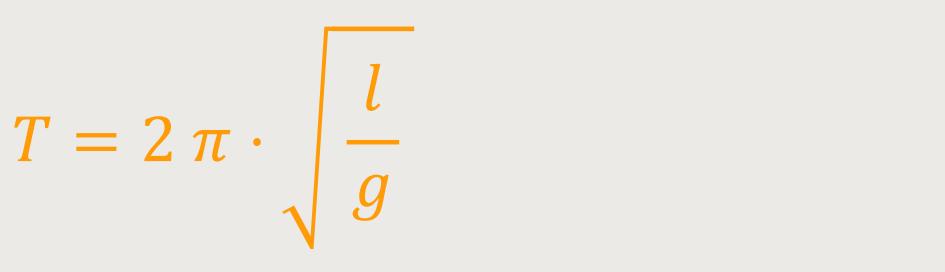
Eine wichtige Schluss­folgerung lässt sich noch aus dem Äquivalenz­prinzip ziehen:

Wenn m = m_s, dann kann man das 2. Newton-Axiom auch schreiben als:

Diese Beziehung beschreibt die Gewichts­kraft in einem homogenen Gravitationsfeld.

Daraus ergibt sich, dass die Gravitations­feld­stärke die Kraft auf die Einheit der schweren Masse ist.

Anderseits haben wir bereits die Bewegungs­gleichung. Nämlich dass Kraft = Masse · Beschleunigung ist.

m   ist hier für die träge Masse (siehe 2. Newton-Axiom)

Das ist wiederum die Bewegungs­gleichung für den freien Fall. Und wenn m = m_s wegkürzt, erhält man.

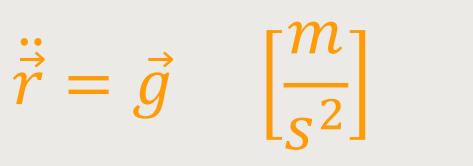
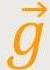  ist die Fallbeschleunigung

Damit erhalten wir die Bestäti­gung, dass die Gravitations­feld­stärke beim freien Fall nichts anderes ist, als die Fall­beschleuni­gung. Dabei ist es unabhängig, was für eine Masse der Körper hat. Und somit fallen alle Körper im Vakuum gleich schnell.

In unserem Fall gilt das für ausreichend kleine Systeme in der Nähe der Erdober­fläche.

Die Dimension für die Fallbe­schleunigung leitet sich wie folgt her:

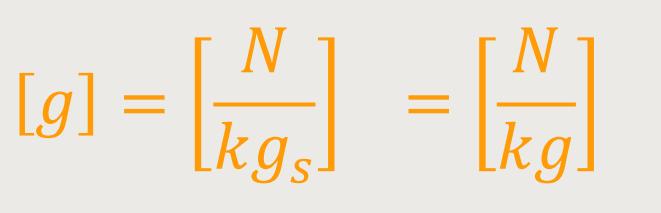
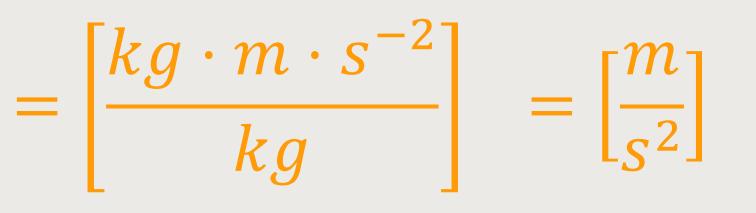
Die Gravitations­feld­stärke wurde ja zunächst definiert, als die Kraft auf die Einheit der schweren Masse. Dann wurden die Einheiten von schwerer und träger Masse gleich­gesetzt. Wenn man anschlie­ßend die Einheit der Kraft entspre­chend ausformuliert und abschlie­ßend weg­kürzt, erhält man die Dimension m /s^₂.

⇦ Kapitel Kapitel ⇨