Wie wir bereits gesehen haben, ist es bei dem Arbeits­begriff so, dass eine Arbeit an einem System verrichtet wird. Diesem System wird entweder Arbeit zugeführt, oder falls sie negativ ist, dem System abgeführt. Dagegen ist der Energie­begriff, den wir uns aus dem Arbeits­begriff abgeleitet haben, eine „System­eigenschaft”. Man geht also davon aus, dass das jeweilige System diese Energien besitzt. Das bedeutet, die Arbeit ist ein „Grenz­flächen­konzept”. Mit anderen Worten, über die Grenz­fläche zwischen der Umgebung und dem System wird Arbeit verrichtet. Dagegen ist die Energie, egal ob kinetische und potentielle, eine System­eigenschaft, die dem System zugerechnet ist.

Das „Noether-Theorem”, benannt nach der Mathematikerin Emmy Noether, sagt aus:

Die Erhaltungs­sätze sind eine Folge der Invarianz Eigenschaften.

Diese „Invarianz Eigen­schaften” sind in der Natur ein ganz wesent­licher Aspekt. Sie werden oft auch als „Symmetrien” bezeichnet. So sind zum Beispiel die Invarianz bei Translation im Raum und die grund­legenden Gesetz­mäßig­keiten in der Natur dieselben. Diese Invarianz gegen­über Trans­lationen hat die „Impuls­erhaltung” zur Folge. Die Invarianz gegen Drehungen bzw. gegen Rotation, hat die „Dreh­impuls­erhaltung” zur Folge.

Und die Invarianz hinsicht­lich der Trans­formation von einem Inertial­system auf ein anderes Inertial­system, ob man beispiels­weise die Welt aus einem stehenden Zug oder aus einem gleich­förmig gerad­linig bewegten Zug betrachtet, ändert nichts an der Gültig­keit der Natur­gesetze. Diese Invarianz hat die Erhaltung des „Massen­mittel­punkt­impulses” zur Folge.

Und letztlich folgt der „Energie­erhaltungs­satz” aus der Invarianz gegen die Zeit­translation. Das bedeutet, dass die Natur­gesetze morgen noch genauso gelten werden wie heute. Das eine solche Invarianz vorhanden ist, hat somit diesen Energie­erhaltungs­satz zur Folge. So wie die Zeit eine einzelne Größe ist, so ist die Energie eine skalare Größe. Dagegen ist der Impuls eine vektorielle Größe, und auch Trans­lationen können in verschie­denen Richtungen durch­geführt werden. Dement­sprechend muss die Energie eine „skalare” Größe sein, weil sie eben der „Zeit­translations­invarianz” entspricht. Daraus folgt:

„Invarianz” ist die Unveränder­lichkeit von Größen.

Zunächst einige generelle Aussagen über „Kräfte und Kraftfelder”.

Wenn man eine ortsab­hängige Kraft betrachtet, die an verschie­denen Punkten unterschied­liche Werte und Richtungen hat, dann spricht man von einem Kraftfeld. Wenn aber der Kraft­vektor ortsunab­hängig ist, handelt es sich um räumlich konstante Kräfte. In diesem Fall handelt es sich um ein spezielles Kraft­feld. Diese Kräfte bilden dann ein sogenanntes „homogenes Kraft­feld”, wie es bereits im vorherigen Kapitel angesprochen wurde.

Eine weitere Form eines speziellen Kraft­feldes sind die auf ein Kraft­zentrum gerichteten Kräfte. Solche Kräfte nennt man „Zentral­kräfte”. Beispiels­weise das Kraft­feld in der Umgebung der Sonne, oder auch das Kraft­feld in der Umgebung einer Punkt­ladung. Beide sind dadurch charakte­risiert, dass der Kraft­vektor immer parallel zum Orts­vektor ist. Dabei wird natur­gemäß der Ursprung des Koordinaten­systems ins Kraft­zentrum gelegt. Und dann ist der Kraft­vektor immer parallel zum Orts­vektor: || .

Und wenn Kräfte zeitunab­hängig sind, sich also im Laufe der Zeit nicht ändern, dann spricht man auch von „statischen Kräften”. Wie muss man sich jetzt ein solches Kraft­feld vorstellen?

Da gibt es grund­sätzlich zwei Denkmöglich­keiten. Möglich­keit eins ist eine Fern­wirkung. Das also automatisch und sofort und in alle Instanzen augen­blicklich eine Kraft­wirkung vorhanden ist. Und wenn räumliche Distanzen keine Rolle spielen, nennt man das „Fern­wirkungs­kräfte”.

Wir sprechen hier aber im Wesent­lichen von „Nahwirkungs­kräften”. Der Unter­schied ist nicht zu vernach­lässigen. Im Fall von Nahwirkungs­kräften wird die Kraft­wirkung durch einen lokalen Zustand des umgebenden Raumes bewirkt. Hierbei kann sich der Zustand des Raumes ausbreiten, wie das zum Beispiel bei elektro­magnetischen Wellen der Fall ist.

Noch interessanter wird es, wenn sich heraus­stellt, dass dieser Zustand des Raumes sogar Energie enthalten kann. Denn wenn sich so ein Zustand wellen­förmig ausbreitet, wie beispiels­weise bei den Licht­wellen, dann wird mit dieser Ausbreitung auch Energie trans­portiert. Durch diese Über­legung ist es möglich, die elektro­magnetische Wechsel­wirkung und ihre zeit­liche Aus­breitung quantitativ zu beschreiben.

Bei der Gravitation ist es komplizierter. Man spricht zwar auch von Gravitations­wellen, die aber zurzeit experimentell noch schwer nachzuweisen sind.

Welche Kräfte haben wir denn überhaupt in der Natur? Interessanter­weise gibt es da gar nicht so viele unter­schiedliche Kräfte. Was wir gegen­wärtig sagen können ist, dass wir je nach Sichtweise drei bis vier unter­schiedliche Kräfte haben.

Wenn wir sie nach der Stärke ordnen, ergeben sich:

Die relative Stärke dieser Kraft ist 10⁻¹. Die Reich­weite ist mit nur 10⁻¹⁵m sehr kurz.

Die „starke Wechsel­wirkung” ist dafür zuständig, dass die Atomkerne, die aus den positiv geladenen und den neutralen Teilchen bestehen, nicht auseinander­fliegen. Da gleich­namige Ladungen einander abstoßen, hält die starke Wechsel­wirkungs­kraft die Welt im Innersten zusammen. Aber bereits in Dimensionen jenseits der Atomkern­dimension ist diese Wechsel­wirkung nicht mehr spürbar, sodass die Elektronen­hülle davon praktisch nicht betroffen ist. Somit ist sie eine Kraft von kurzer Reichweite.

Die „elektromagnetische Wechsel­wirkung” hat eine Kopplungs­konstante 1 / 137 (ca. 10⁻²). Also gar nicht so viel schwächer als die starke Wechsel­wirkung. Die Reich­weite ist aller­dings unendlich.

Die „schwache Wechsel­wirkung” hat eine Kopplungs­konstante von 3× 10⁻⁷. Ihre Reich­weite ist extrem klein, ja so klein, dass man sie gar nicht quantitativ fest­stellen kann. Man weiß nur, sie ist kleiner als 10⁻¹⁸m.

Ohne eine derartige Wechsel­wirkungs­kraft könnte man den Beta-Zerfall nicht beschreiben.

Die „Gravitations-Wechsel­wirkung” hat eine Kopplungs­konstante von 5× 10⁻³⁹. Sie ist zwar sehr klein, aber ihre Reich­weite ist, wie man bis jetzt vermutet, eben­falls unendlich.

Bei der Gravitation hat man es mit verhältnis­mäßig großen Massen zu tun. Man sagt, die Gravitation ordnet die Vorgänge im Kosmos. Während die Wechsel­wirkungen mit geringen Reich­weiten die Vorgänge im nuklearen Bereich ordnen. Die elektro­magnetische Wechsel­wirkung sticht dabei heraus. Denn sie reicht einer­seits unendlich weit und ist trotzdem von verhältnis­mäßig großer Stärke. Und dennoch ist sie nicht die alles beherrschende Wechsel­wirkung. Warum ist das so? Aus einem wichtigen Grund ist das nicht so.

Die Gravitation hat nämlich sozusagen nur eine Ladung. Massen können sich immer nur anziehen und werden sich „nie” abstoßen. Während es bei den elek­trischen Ladungen so ist, dass es positive und negative Ladungen gibt. Die ungleich­namigen Ladungen ziehen einander an und die gleich­namigen stoßen einander ab. Das bedeutet, wenn man eine ausreichende Anzahl von großen Systemen betrachtet, gibt es dort aufgrund der statistischen Kompensation weitest­gehend ungefähr gleich viele positive wie negative Ladungen innerhalb des Systems. Somit werden, wenn man große Systeme betrachtet, keine nennens­werten elektro­magnetischen Wechsel­wirkungen auftreten. Erst wenn es einem gelingt, Ladungen zu trennen, treten solche Kräfte auf.

Letztlich kann man die elektro­magnetische und die schwache Wechsel­wirkung zu einer „Elektro­schwachen Kraft” zusammen­fassen. Hierzu versucht man, sie in einer gemein­samen theore­tischen Struktur zu beschreiben.

Betrachten wir eine dieser Grundkräfte etwas genauer.

Es ist eine experimen­telle Tatsache, dass Körper in einem Schwere­feld, also einem Gravitations­feld, eine Kraft erfahren. Und so wie man das generell in der Physik macht, versucht man beschreibend an die Dinge heran­zugehen. Und so gehen wir davon aus, dass diese Gewichts­kraft proportional sein wird, zu einem Parameter der diesen Körper beschreibt, nämlich zur sogenannten schweren Masse.

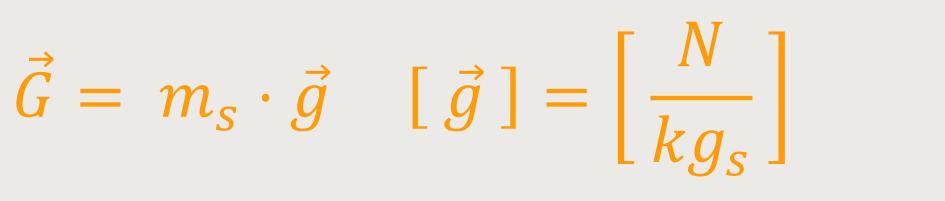
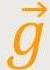  ist die schwere Feld­stärke
m_s   ist die schwere Masse

Daher ist die schwere Feld­stärke das Gewicht pro Einheit der schweren Masse (das Gewicht der Massen­einheit). Sie beschreibt die Eigen­schaft des Feldes unabhängig davon, wie groß die jeweilige Masse ist, die in einem solchen Feld beein­flusst wird. Die schwere Feld­stärke 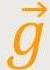wird dann als Vektor geschrieben. Hier auf der Erdober­fläche ergibt sich daraus:

Insgesamt gesehen ist das Gravitations­feld der Erde kein homogenes Kraft­feld. Wenn wir uns aller­dings in einem genügend kleinen System gegen­über dem Erdradius befinden, kann man in guter Näherung dennoch von einem homogenen Feld sprechen.

Grafik (wird später eingefügt)

Die Bewegungsgleichung lautet:

Masse · Beschleunigung = Gewichtskraft

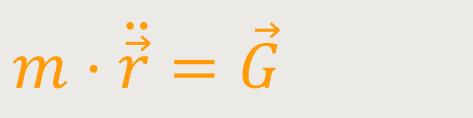
Hinweis:
Hier steht das m für die träge Masse (siehe Newton-Axiom).

Wenn man nun entsprechend einsetzt, erhält man:

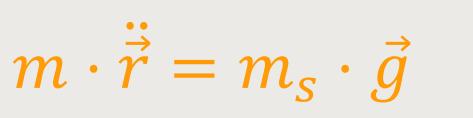
Jetzt folgt die skalare Gleichung für die dritte z-Komponente:

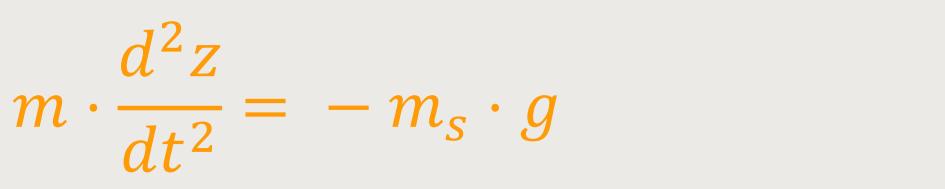
Das kann man jetzt nach der Zeit integrieren:

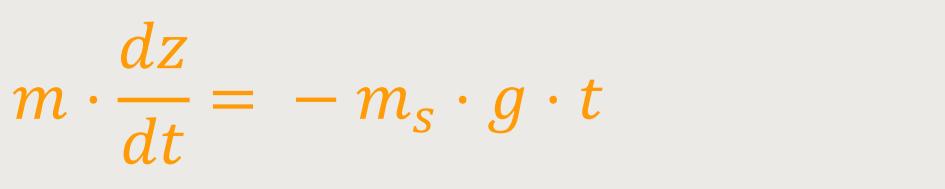
Und wenn man noch einmal nach der Zeit integriert, kommt folgendes heraus:

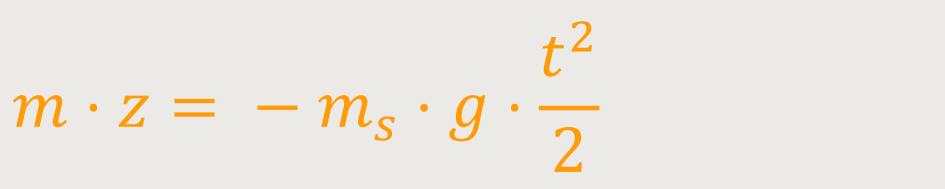
Für eine bestimmte Fallhöhe H gilt unter Berücksichtigung, dass z = −H ist:

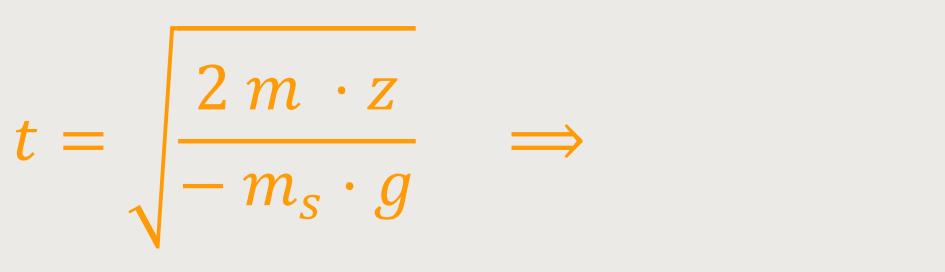
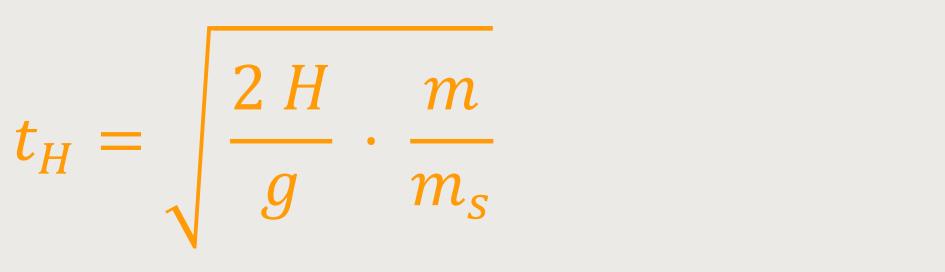
Der Term m /m_s steht für das Verhältnis der trägen Masse zur schweren Masse. Wobei beides gleich­artige Größen sind. Damit erhält man zunächst:

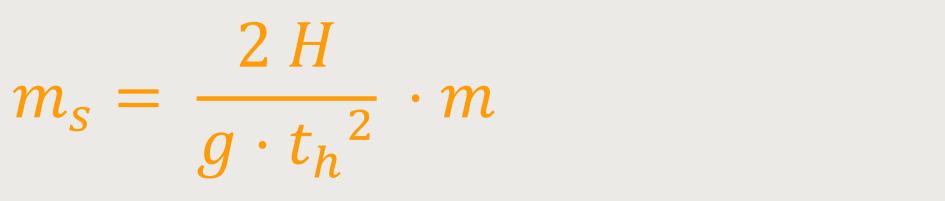
Lässt man zwei Körper aus unter­schiedlichen Höhen in einem Gravitations­feld fallen, so fallen beide Körper immer gleich schnell. Voraus­gesetzt natürlich, man lässt die Luft­reibung unberück­sichtigt. Mit der allge­meinen Relativitäts­mechanik, wo die Gravitations­kräfte auf Trägheits­bewegungen in einem gekrümmten 4-dimensionalen Raum-Zeit-Kontinuum zurück­geführt werden, lässt sich das genauer beschreiben.

Und wenn Körper stets gleich schnell fallen, dann muss der Faktor zwischen der trägen und der schweren Masse konstant sein. In diesem Fall ist dieser Faktor eine universelle Konstante.

2 H /(g · t_h²) wäre dann diese universelle Konstante und man könnte somit auch schreiben:

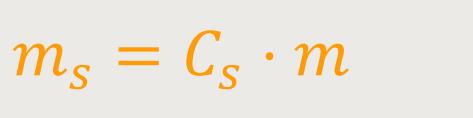
C_s   ist eine universelle Konstante

Nun nimmt man an, dass m und m_s gleich­artige Größen sind. Das nennt man auch das „Äquivalenz­prinzip”. Und deshalb wählt man die Ein­heiten so, dass für die universelle Konstante der Wert Eins herauskommt. Man setzt somit beide Größen gleich:

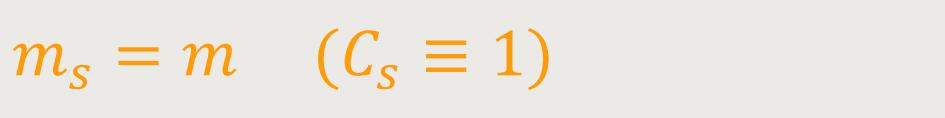
Und damit kann man die Fallzeit konkret ausrechnen:

Des Weiteren lässt sich auch die Gravitations­feld­stärke berechnen.

Durch experimentelle Versuche kann man abschließend folgende Festlegung treffen:

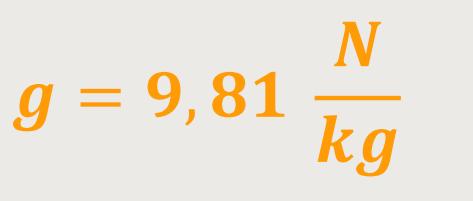
Hinweis:
Die Schwerebeschleunigung beträgt 9,832 m/s² an den Polen und 9,780 m/s² am Äquator.

Mit einer Verdop­pelung der Masse erfolgt auch immer eine Verdop­pelung der Trägheit. Und aus der Fall­zeit eines Körpers ergibt sich unmittelbar:

Die Kraft, mit der eine Masse von 1 kg von der Erde ange­zogen wird, beträgt 9,81 N.

Eine gute Methode, sich die Gravitations­kraft verständ­lich zu machen, geschieht mithilfe der Pendel­schwingung. Wie bereits angekündigt, gehen wir jetzt näher darauf ein.

⇦ Kapitel Kapitel ⇨