Wozu schaut man sich denn über­haupt „Bezugs­systeme” an, und vor allem bewegte Bezugs­systeme? Generell ist es so, dass man sich bemüht, Koordinaten­systeme (Bezugs­systeme) so zu wählen, dass sie dem jewei­ligen System, welches man unter­suchen möchte, möglichst gut angepasst sind. Es bestand aber nicht immer Einig­keit über das gewählte Bezugs­system. Soll man zum Beispiel das geozen­trische oder das heliozen­trische System zugrunde legen? Aus Sicht der klassischen Physik sind beide gleich­berechtigt. Aber meistens ist es praktischer, das heliozen­trische System zu verwenden. Wenn man jedoch weiß, wie man auf bewegte Bezugs­systeme trans­formiert bzw. umwandelt, kann man das eine in das andere über­führen.

Bei der weiteren Betrachtung kommt zusätz­lich das Konzept der Trägheits­kräfte vor. Wenn wir dort von einem Bezugs­system sprechen, verstehen wir darunter die „kartesischen Koordinaten”.

Das System S hat als Koordinaten­system den Ursprung O und als Basis­vektoren _x, _y, _z (Dach bedeutet, dass es sich um Einheits­vektoren handelt). Und die Vektoren stehen alle paar­weise senk­recht aufein­ander. Des Weiteren setzten wir voraus, dass das System S ein Inertialsystem ist.

Das zweite System S^∗, auf welches man trans­formiert, hat als Koordinaten­system den Ursprung O^∗ und als Basis­vektoren _x^∗, _y^∗, _z^∗. Das System S^∗ kann sich sowohl „transla­torisch”, also geradlinig bewegen, als auch „räumlich” wegdriften.

Wir werden nun verschiedene Bewegungs­arten betrachten.

Bei dieser Bewegungsart setzt man voraus, dass sich O^∗ relativ zu O bewegt. Und zu der Zeit t = 0 sollen beide Systeme im Ursprungs­punkt vereinigt sein.

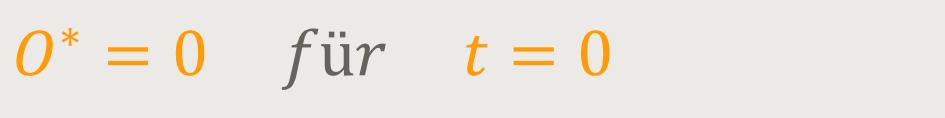
Die Basis­vektoren sind alle parallel und sie bewegen sich immer parallel zueinander.

Zwischen beiden Koordinaten­ursprüngen O und O^∗ gibt es einen Verbindungs­vektor . Und wenn man jetzt im Raum irgen­deinen Massenpunkt P betrachtet, dann kann man diesen Punkt aus der Sicht des einen Systems O und aus der Sicht des anderen Systems O^∗ betrachten. Im System O lautet der Orts­vektor dann . Dagegen lautet im System O^∗ der Orts­vektor ^∗. Man kann sofort erkennen, wie diese beiden Vektoren zusammen­hängen:

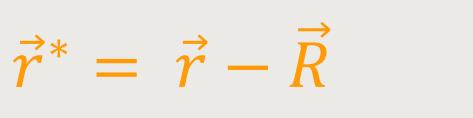
Wie verhält es sich nun bei gleichförmig bewegten Bezugs­systemen?

Der Verbindungs­vektor verbindet beide Bezugs­systeme mit­einander und steht für die transla­torische Bewegung. Da es sich jetzt um eine gleich­förmige Bewegung handelt, bewegt sich das System O^∗ mit einer konstanten Geschwindig­keit. Anders ausge­drückt, das System O^∗ bewegt sich mit konstanter Geschwindig­keit relativ zum System O. Der Geschwindig­keits­vektor, welchen wir jetzt nennen, gibt die Geschwindig­keit von O^∗ relativ zu O an. Wobei dieses = const ist.

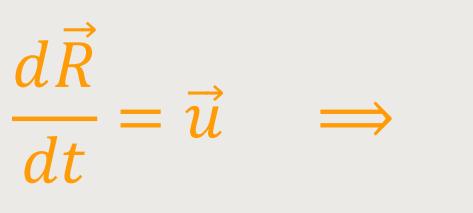
Wenn die Geschwindig­keit von O^∗ relativ zu O ist, und der Orts­vektor des anderen Ursprungs in Bezug auf das ursprüng­liche Koordinaten­system ist, dann folgt daraus wenn man integriert:

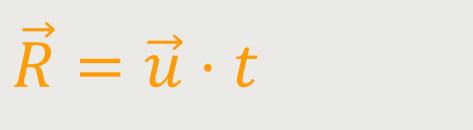
Nach Einsetzen ergibt sich sofort ein Zusammen­hang zwischen den beiden Beziehungen:

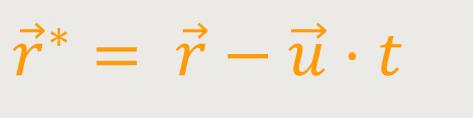
Aller­dings muss dazu gesagt werden, dass die Zeit in dem einen System gleich der Zeit in dem anderen System ist:

In der klassischen Mechanik ist das eine Selbst­verständlich­keit. In der relativis­tischen Mechanik dagegen zeigt sich, dass das nicht zwangs­läufig der Fall ist.

Obige Trans­formation von und t zu ^∗ und t^∗ ist die soge­nannte „Galilei-Transfor­mation”. Voraus­setzung ist hierbei, dass es sich um zwei gleich­förmig bewegte Bezugs­systeme handelt.

Und die damit in Zusammen­hang stehende Lorenz-Transfor­mation ist dann nichts anderes, als eine Verallge­meinerung dieser Transfor­mation auf hohe Geschwindig­keiten. Wenn also das sehr groß wird, zum Beispiel in die Nähe der Licht­geschwindig­keit kommt, dann stimmt die Berechnung nicht mehr. Dazu reicht die klassische Physik nicht aus. Deshalb trifft unsere Betrachtung vorerst nur zu, wenn die Geschwindig­keiten im Verhältnis zur Licht­geschwindig­keit klein sind.

Dennoch hat die Galilei-Transfor­mation eine wichtige Bedeutung als Ausgangs­punkt für die Relativitäts­mechanik. Und wenn man die relativis­tischen Formeln hernimmt, und diese für kleine Geschwindig­keiten zugrunde legt, dann ergibt sich mit aller Genauig­keit wieder obige Gleichung.

Zunächst werden wir jetzt die dazuge­hörige Geschwindig­keit ausrechnen.

Um welche „Geschwindig­keit” wird es gehen? Wir haben ja zwei Bezugs­systeme. Man kann die Geschwindig­keiten bezüg­lich des Systems S und des Systems S^∗ betrachten. Zunächst geht es um einen Massen­punkt, das heißt ein Teil­chen oder einen Körper, welches sich im Raum mit einer Geschwindig­keit bewegt. Und wir schauen uns an, wie groß seine Geschwindig­keit relativ zu S und relativ zu S^∗ ist.

Die Geschwindig­keit relativ zu S bezeichnet man wieder mit , und das entspricht:

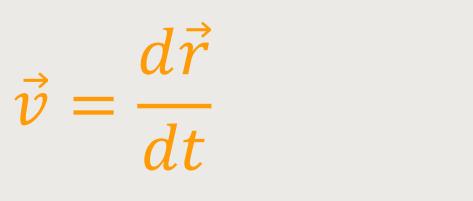
Man kann die Geschwindig­keit natürlich auch relativ zu S^∗ betrachten, und die nennt man dann _rel, und das entspricht:

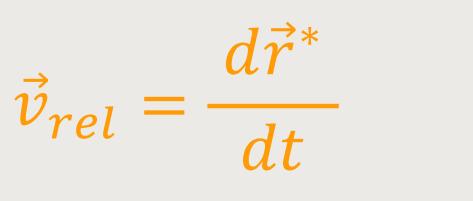
Das sieht im Moment noch alles sehr einfach aus. Doch bei beschleu­nigten und rotierenden Systemen ist es nicht mehr ganz so einfach.

Möchte man konkret die Geschwindig­keit ermitteln, sieht das wie folgt aus:

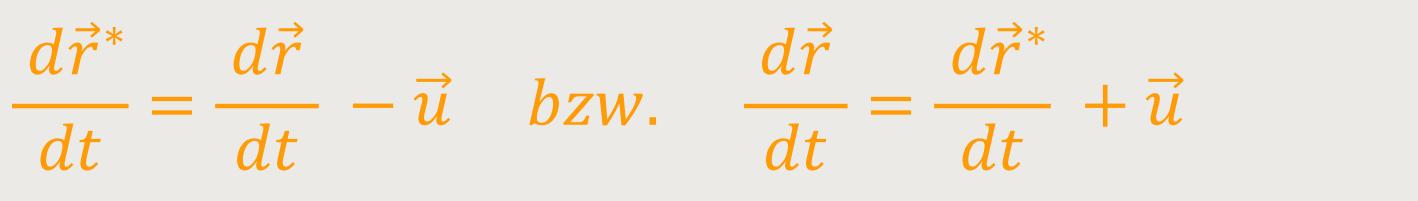
Also, die Relativ­geschwindig­keit des Körpers relativ zu dem System S^∗ ist gleich die Geschwindig­keit relativ zu S minus .

Hier sei nochmals erwähnt, dass die Relativ­geschwindig­keit der Bezugs­systeme ist, während die Geschwindig­keit des Massen­punktes ist.

Daraus kann man nun die „Beschleu­nigung” berechnen.

Wenn man die vorherige Gleichung nochmals nach der Zeit ableitet, ergibt sich:

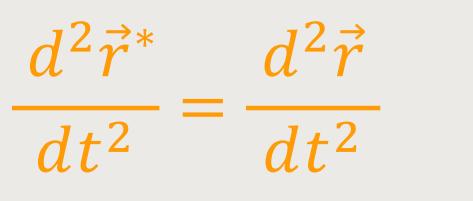
Aus Sicht der beiden Systeme sind beide Beschleu­nigungen gleich. Also, wenn sich ein System relativ zu einem Inertial­system gleich­förmig bewegt, ist es seiner­seits wieder ein Inertial­system.

Wie sieht es aber mit gleich­förmig beschleu­nigten Bezugs­systemen aus? Zunächst betrachten wir wieder die Translation.

⇦ Kapitel Kapitel ⇨