Um den Begriff der „Energie” einzu­führen, gehen wir in zwei Schritten vor. In der Mechanik gibt es zwei unter­schied­liche Arten von Energie. Zum einen spricht man von der „kinetischen Energie”. Diesen Begriff führt man zurück auf den Begriff der Arbeit. Dabei betrachtet man ein Teil­chen bzw. einen Massen­punkt, der sich mit einer gewissen Geschwindig­keit bewegt. Die kinetische Energie, die man diesem Teil­chen zumisst, ist diejenige Arbeit, die verrichtet werden musste, um diesen Körper aus anfäng­licher Ruhelage auf eine bestimmte Geschwindig­keit zu beschleu­nigen, was letzt­lich unter dem Ein­fluss einer Kraft geschieht. Man spricht dann davon, dass diese Arbeit diesem Teil­chen als kinetische Energie gewisser­maßen über­tragen wurde. Man könnte auch sagen, es wurde Arbeit in ihn investiert.

Also, es ist eine Arbeit, die vorher aufge­wendet werden muss, um einen Körper aus anfäng­licher Ruhe auf die Geschwindig­keit zu beschleu­nigen, die er dann hat. Diese kinetische Energie lässt sich relativ einfach ausrechnen.

Wir werden die Formel Schritt für Schritt herleiten.

Zunächst betrachtet man den Massen­punkt, der zum Zeit­punkt t_₀ am Punkt P_₀ in Ruhe ist. Der Körper hat also in diesem Fall keine Anfangs­geschwindigkeit.

Grundsätzlich berechnet man die Arbeit längs eines Weges von P_₀ nach einem Punkt P_A. Den jeweiligen Punkt P_A, den man zu einem bestimmten Zeit­punkt betrachtet, nennt man auch „Aufpunkt”. Der Körper befindet sich zu der Zeit t = t_A am Punkt P_A.

Die Arbeit T_A ist definiert als:

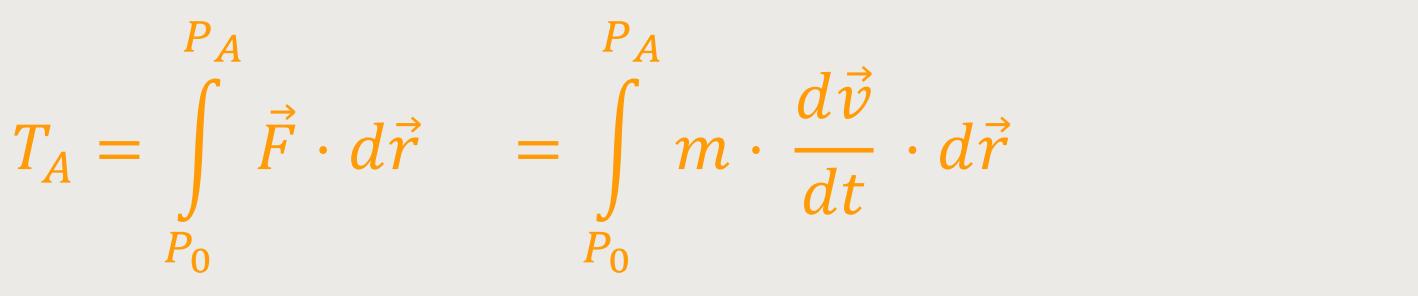
  ist die Kraft, die auf den Körper wirkt

Man erhält hier ein Kurven­integral, welches sich weiter umformen lässt. Das ist dann der Fall, wenn der Kurven­verlauf gegeben ist als „Parameter­darstellung”. Zudem muss man berück­sichtigen, dass der Orts­vektor eine Funktion der Zeit ist. Dann kann man nämlich dieses Integral umformen in ein Integral über die Zeit wenn d / dt gegeben ist. Diese Vorgehens­weise ist bereits bekannt aus den vorherigen Kapiteln.

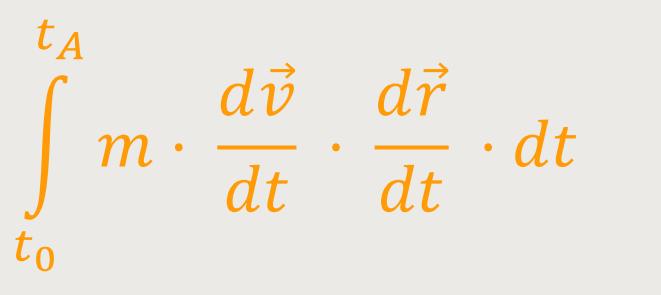
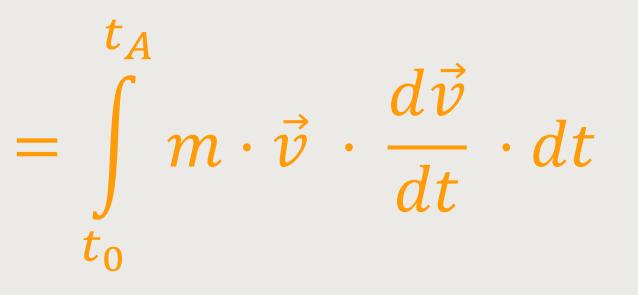
Jetzt benutzt man einen Trick, um weiter umformen zu können. Man überlegt sich, was herauskommt, wenn man folgendes bildet:

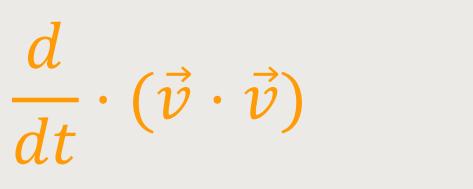
Hier wird der Geschwindig­keits­vektor (als Skalar) mit sich selbst multi­pliziert. Unter Berück­sichtigung der Produkt­regel ergibt sich daraus:

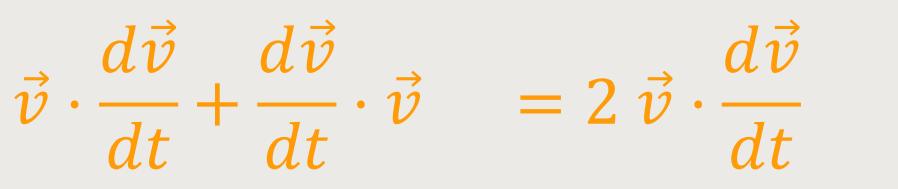
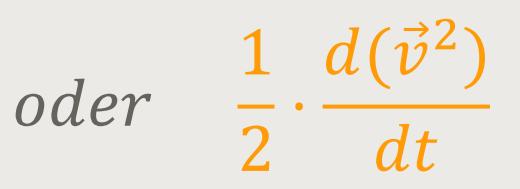
Und das setzt man jetzt entsprechend oben ein:

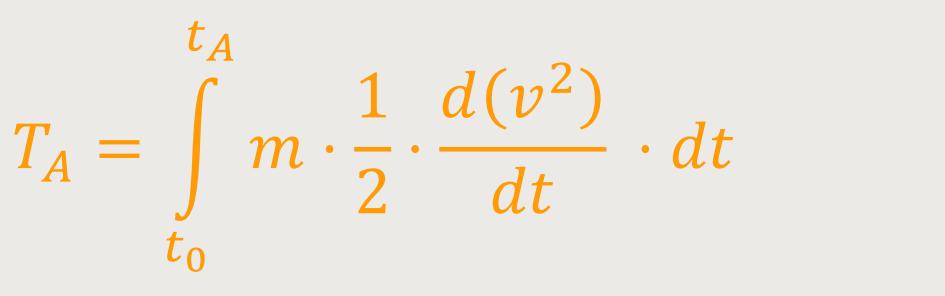
Anschließend folgt nichts anderes als eine Substitution:

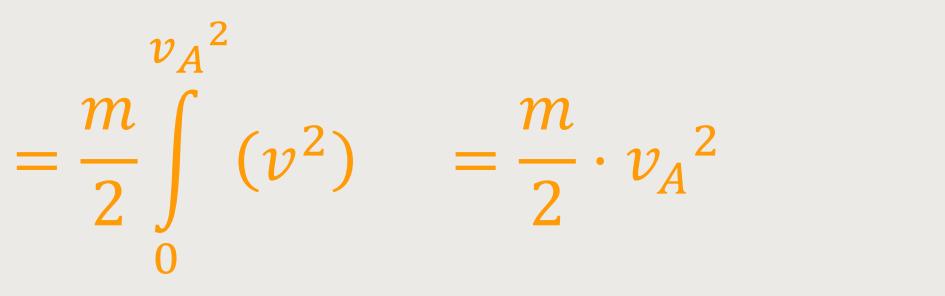
v^₂   ist die Integrationsvariable

Und damit erhält man das Ergebnis für die kinetische Energie:

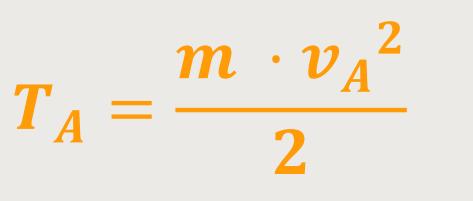
Man erkennt auch, dass die kinetische Energie eines Körpers propor­tional zur Masse ist.

Hinweis:
Aus dem Exponenten ergibt sich: Wenn man die doppelte Geschwindig­keit erreichen möchte, muss man die vierfache Arbeit hineinstecken.

Was ist aber, wenn der Körper bereits eine Anfangs­geschwindigkeit hat?

Jetzt rechnen wir im zweiten Fall wieder die Arbeit längs eines Weges aus, von einem Punkt P_₁ → P_₂, wobei der Körper an dem Punkt P_₁ jetzt die Geschwindigkeit V_₁ und an dem Punkt P_₂ die Geschwindigkeit V_₂ hat.

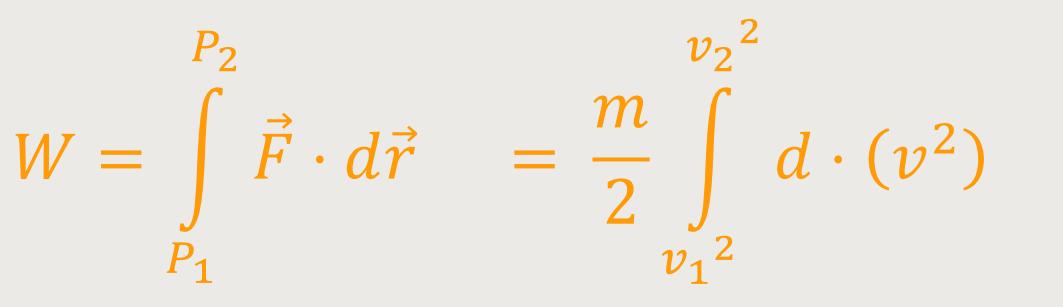
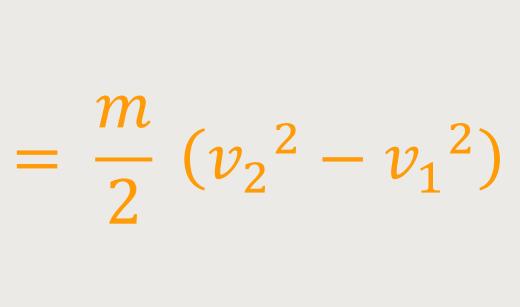
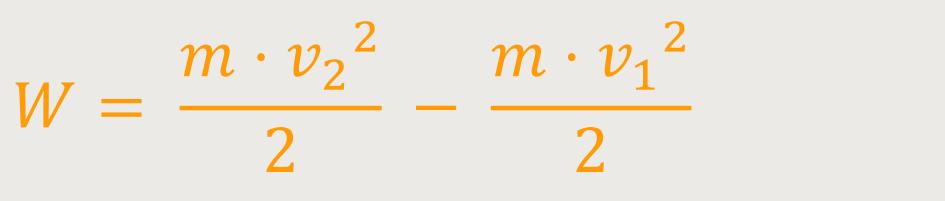
Die Arbeit lässt sich somit aus­rechnen als die Differenz der kinetischen Energien. Gemessen vom Endpunkt „minus” dem Anfangspunkt:

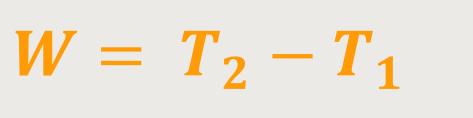
Bevor wir die potentielle Energie betrachten, möchten wir noch kurz über konser­vative Kräfte sprechen.

Wir betrachten im Nach­folgenden einen Körper, bzw. einen Massen­punkt, der sich in einem Kraft­feld befindet, wie zum Beispiel ein Körper an der Erdober­fläche. Das Kraft­feld ist dann das homogene Feld der überall gleichen Gewichts­vektoren im Bereich der Erdober­fläche. Wenn man sich im Verlauf an unter­schiedliche Punkte begibt, werden dort im All­gemeinen auch unter­schiedliche Kräfte wirken. Dieses Kraft­feld wird mit bezeichnet. Hierbei geht es also um spezielle Kraft­felder, die man auch als „konservative Kräfte” bezeichnet.

Unter einem konser­vativen Kraft­feld versteht man ein Kraft­feld, das so beschaffen ist, dass die Arbeit längs jedes geschlos­senen Weges gleich Null ist. Ganz wichtig: Längs geschlos­sener Wege wird keine Arbeit verrichtet. Das bedeutet, dass das Integral · d, integriert über einen geschlos­senen Weg, immer gleich Null ist. Ein solches Ring­integral wird wie folgt definiert:

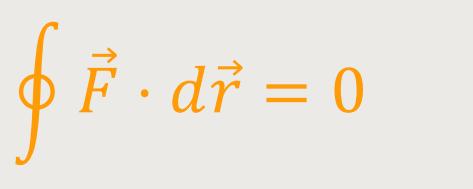
Ein Körper legt also in dem Kraft­feld auf einem geschlossenen Pfad einen Weg zurück, der vom Ausgangs­punkt weg wieder herum verläuft zum Ausgangs­punkt hin. Das bedeutet, dass insgesamt auf diesem Pfad keine Arbeit verrichtet wird. Es kann schon sein, dass eine positive Arbeit verrichtet wurde, in dem Sinn, dass etwas hinein­investiert wurde. Aber es wird im weiteren Verlauf auch wieder eine negative Arbeit entstanden sein, um den Anfangs­effekt wieder rück­gängig zu machen, so dass am Ende die gesamt Arbeit gleich Null ist.

Als Beispiel könnte man die Bewegung der Erde um die Sonne anführen. Der Planet bewegt sich auf einer ellip­tischen Bahn. Auf dieser Bahn­kurve wird Arbeit verrichtet, wenn er sich ein Stück von der Sonne weg bewegt. Wenn er sich aber wieder der Sonne annähert, also den ganzen Zyklus durch­laufen hat, ist die gesamte Arbeit letztlich gleich Null. Wäre das nicht so, würde die Erde in Richtung Sonne hineinspiralen.

Wichtiger Hinweis:
Die Reibungskräfte sind keine konser­vativen Kräfte. Auch die magne­tischen Felder in der Umgebung von strom­umflossenen Leitern sind keine konservativen Felder.

Jetzt wenden wir uns der „poten­tiellen Energie” zu. Unter der poten­tiellen Energie versteht man einen Körper, der unter dem Einfluss einer Kraft steht.

Mit anderen Worten, wir gehen jetzt davon aus, dass sich ein Körper (ein Massen­punkt) in einem Kraft­feld befindet. Des Weiteren nehmen wir an, dass es ein konser­vatives Kraf­tfeld ist. Und der Massen­punkt befindet sich in unserem Beispiel an einem Punkt P.

Um die potentielle Energie an diesem Punkt definieren zu können, muss man zunächst einmal einen unveränder­lichen Bezugs­punkt P_₀ festlegen. Anschließend kann man die poten­tielle Energie eines Massen­punktes definieren, der sich während seines Umlaufs an irgend­einem Punkt P befindet, unter Bezug­nahme des festen Bezugs­punktes P_₀. Das ist einfach nichts anderes als die Arbeit, welche die Kraft verrichten kann, falls sich der Massen­punkt von seinem Punkt P, wo er gerade ist, nach diesem Bezugs­punkt P_₀ hin bewegt: P → P_₀

Die Betonung liegt auf „falls”. Denn es steht eine poten­tielle Energie zur Verfügung, die aber nicht immer sofort abgerufen wird. Sie kann zum Beipsiel abgerufen werden durch die Schwer­kraft. Daher kann man diese poten­tielle Energie abschließend recht einfach aufschreiben.

Diese potentielle Energie ist somit nichts anderes als die Arbeit, die verrichtet werden kann, wenn sich der Massen­punkt von P → P_₀ bewegt.

Abschließend lässt sich Ganze noch mit einem „Minus” umformen:

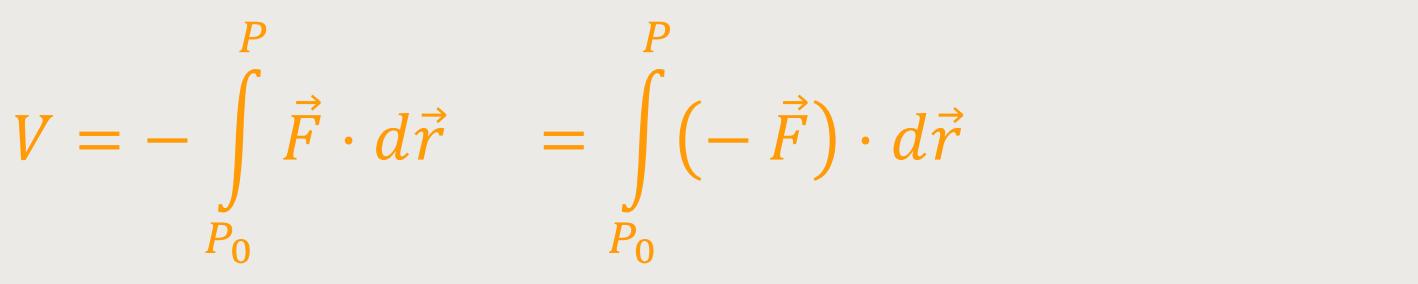
Diese negative Kraft − ist eine Gegen­kraft zu der wirkenden Kraft .

Man kann auch sagen, diese poten­tielle Energie kann aufge­fasst werden als die Arbeit, die von einer Gegen­kraft gegen die wirkende konser­vative Kraft verrichtet wird, wenn man vom Bezugs­punkt zum betrach­teten Punkt aufsteigt. In der Weise wird es auch häufig erklärt.

Man kann die potent­ielle Energie so veranschau­lichen, dass man mit der Muskel­kraft, das ist die Gegen­kraft gegen die Gewichts­kraft, einen Gegen­stand längs einer Bahn­kurve vom Boden aufhebt und auf einen Tisch legt. Letzten Endes ist das dieselbe Arbeit, die anderer­seits von der Schwer­kraft verrichtet wird, wenn der Körper sich wieder hinunter bewegt, vom Tisch zum Boden. Der Boden ist der Bezugs­punkt und auf dem Tisch ist der Punkt P, um den es geht.

Warum wurde das Ganze auf konser­vative Kraft­felder einge­grenzt? Weil hier keine Fest­legung erfolgt ist, längs welchen Weges man sich bewegt, vom Punkt P, wo man sich gerade befindet, zum Bezugs­punkt P_₀.

Diese potentielle Energie ist nur dann ein­deutig, wenn der Ausdruck für die Kraft nicht abhängig ist vom konkreten Verlauf der Bahn­kurve. Hat man die Freiheit, verschiedene Bahn­kurven zu wählen, dann kommen dement­sprechend unter­schied­liche Werte für dieses Intergral heraus. In diesem Fall ist die poten­tielle Energie gar nicht so eindeutig definiert.

Das heißt, eine poten­tielle Energie, als Punkt­funktion, kann nur dann ein­deutig definiert werden, wenn das Kraft­feld, in welchem sich der Körper befindet, ein konser­vatives Kraft­feld ist. Dann aller­dings ist die poten­tielle Energie eindeutig und eine sehr nützliche Größe.

⇦ Kapitel Kapitel ⇨