Im vorherigen haben wir die Massen­anziehung zweier Punkt­massen betrachtet. Abschlie­ßend hatten wir das Newton'sche Gravitations­gesetz in einer vektoriellen Form aufge­schrieben. Jetzt wollen wir untersuchen, ob wir hier eine potentielle Energie einführen können.

Wie wir bereits gesehen haben, hängt die Kraft und die potentielle Energie zusammen:

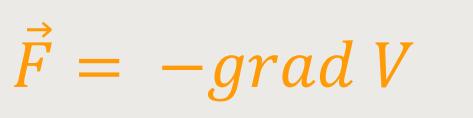
Durch Gradientenbildung dieser potentiellen Energie, die ja selbst eine skalare Orts­funktion ist, erhält man diese Kraft.

Zunächst kann man den Gradienten der Größe 1/r betrachten:

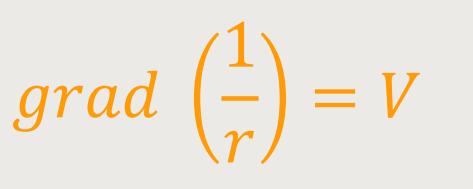
r   ist der Abstand vom Ursprung.

Und das ist nichts anderes als:

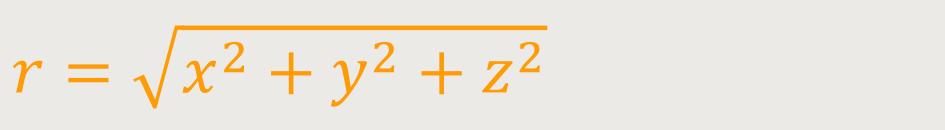
Die Komponenten des Orts­vektors sind die Koordinaten des Punktes, an dem man sich gerade befindet, also x-y-z. Daraus ergibt sich:

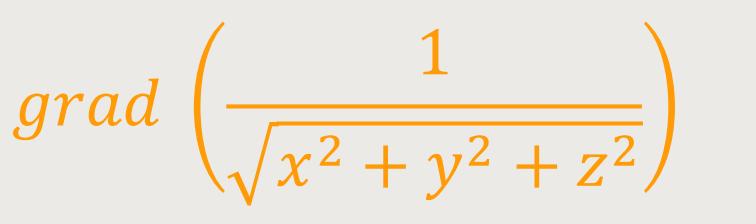
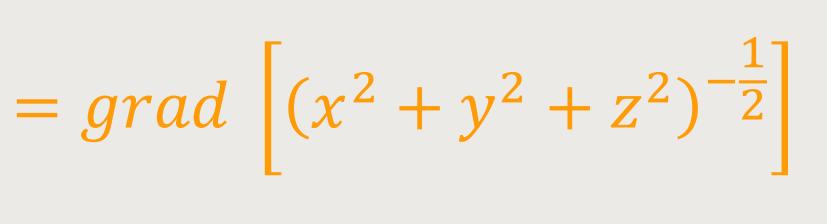
Der Gradient ist ein Vektor­operator, das heißt es werden einfach die partiellen Ableitungen, nach d_x, nach d_y und nach d_z gebildet.

Und wenn man dabei auf die Kettenregel achtet, kommt heraus:

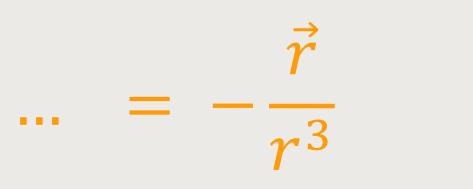
Und dann sieht man sofort, dass man für diese potentielle Energie einen einfachen Ausdruck findet, der das beschreibt was wir für die weitere Betrachtung benötigen.

Als Folgerung erhält man für die potentielle Energie:

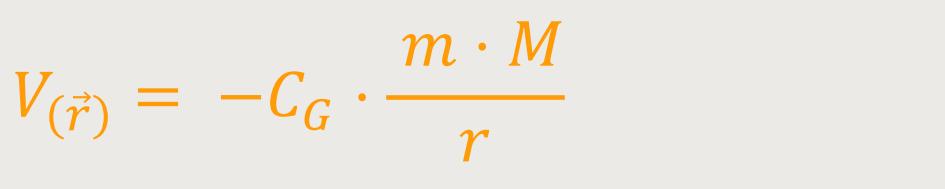
C_G   ist die Gravitationskonstante

Dieses C_G, m und M sind lauter konstante Größen. Wenn man also den Gradienten von dieser potentiellen Energie bildet, erhält man analog zu oben:

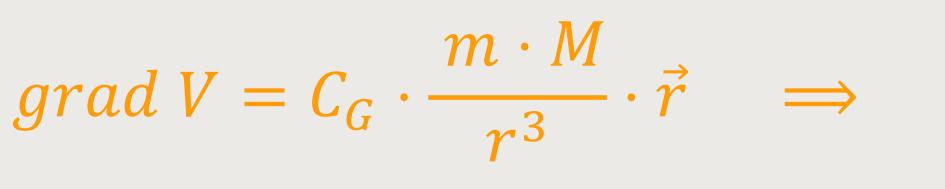
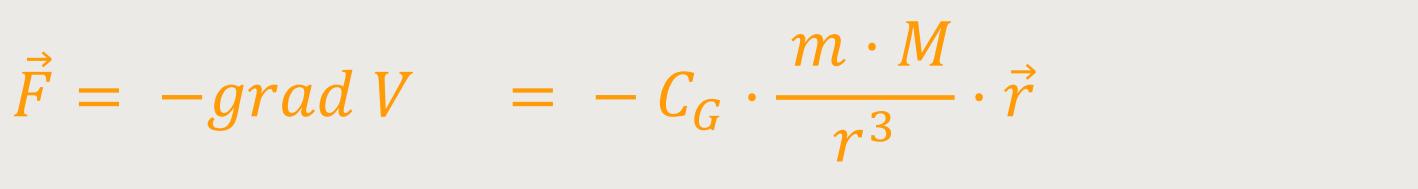
Die potentielle Energie im Gravitationsfeld ist daher:

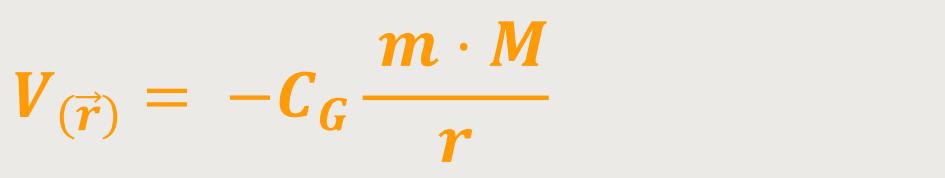
Das Gravitationsfeld in der Umgebung einer Punkt­masse ist demnach ein konser­vatives Kraftfeld.

Wenn der Abstand r gegen unendlich geht, wird die potentielle Energie V gegen Null gehen, bzw. sie wird sukzessive umge­wandelt in kinetische Energie.

Bei Herannahen an die feld­erzeugende Masse wird die Gravitations­kraft immer größer. Wenn man sagt, eine Wechsel­wirkungs­kraft habe unend­liche Reich­weite, dann bedeutet das, dass die zugehörige potentielle Energie nicht stärker als mit 1/r abfällt, sobald man sich von der Punkt­masse entfernt. Dann spricht man von unend­licher Reichweite.

Hinweis: Die potentielle Energie am Bezugspunkt ist Null, das heißt der Bezugs­punkt liegt im Unendlichen.

Daher kann man den Punkt der großen Masse gar nicht in den Bezugs­punkt hinein­legen. Und die nächste vernünftige Über­legung ist, ihn weit weg Richtung unend­lich zu schieben.

Nehmen wir an, wir betrachten zwei Massen, von denen die eine Masse die andere anzieht. Dann zieht umgekehrt die zweite Masse auch die erste an. Und wenn sich die eine durch die Anziehung in Bewegung setzt, müsste die zweite dies ja auch tun. Wie behandelt man eine solche Situation?

Bei der Erde ist das relativ einfach. Als Mensch zieht man die Erde zwar auch an, aber aufgrund der großen Masse ist die Erde so träge, dass dies keine Wirkung hervor­ruft. Genau­genommen fällt die Erde auch auf den anderen fallenden Körper. Nur wegen der größeren Masse viel weniger weit.

Nehmen wir zum Beispiel ein Doppelstern­system mit vergleich­baren Massen, wo sich beide bewegen. Wie lässt sich so etwas beschreiben?

Um das zu visuali­sieren, wendet man sich dem soge­nannten „Zweikörper­problem” zu. Das ist ein ganz wichtiges Problem in der Physik im Allge­meinen und bei der Gravitations­kraft im Besonderen. Ein wesent­licher Punkt ist, um dieses Zweikörper­problem richtig zu verstehen, dass man zunächst zwei Körper beschreibt, die mitein­ander in Wechsel­wirkung stehen. Gemäß Newton III sind diese Wechsel­wirkungs­kräfte so beschaffen, dass die Kraft von dem einen auf den anderen Körper und umge­kehrt die Kraft von dem anderen auf den ersten, entgegen­gesetzt gerichtet sind, aber den gleichen Betrag haben. Der Betrag der Kraft ist zwar jeweils die Gleiche, aber die Trägheit der Masse ist eine andere.

Man betrachtet also zwei Massen m_₁ und m_₂, die gleich­berechtigt sind.

Jetzt kann man die zugehörigen Bewegungs­gleichungen aufstellen, wobei der Einfluss äußerer Kräfte außen vor bleibt.

Zuerst wendet man Newton II auf die Masse m_₁ an:

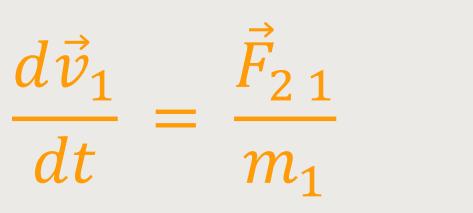
Dann wendet man Newton II auf die Masse m_₂ an:

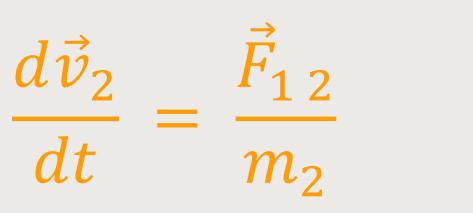
Für oben gilt: Masse · Beschleunigung = wirkende Kraft

Im Grunde sind das zwei gekoppelte Bewegungs­gleichungen, die mitein­ander zusammen­hängen. In Wirklich­keit sind das „gekoppelte Differenzial­gleichungen”. Nun versucht man, wo es geht, sie zu „entkoppeln”. In diesem Fall gibt es eine sehr scharf­sinnige Idee, wie man das umsetzen kann. Und zwar, indem man diese beide Differenzial­gleichungen einfach voneinander abzieht.

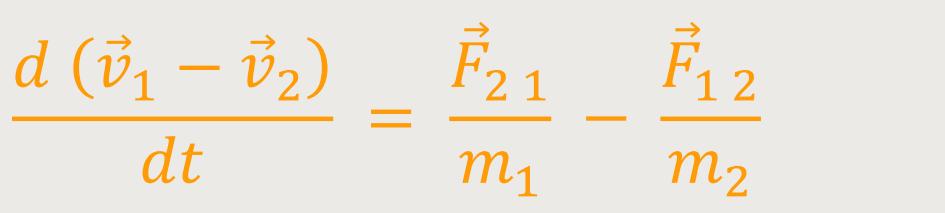
Anschließend lässt sich das noch etwas umformen, indem man zunächst dieses (_₁ − _₂ ) durch die Relativ­geschwindig­keit ersetzt. Denn die Differenz der beiden Geschwindig­keiten ist die Relativ­geschwindig­keit des einen relativ zum anderen:

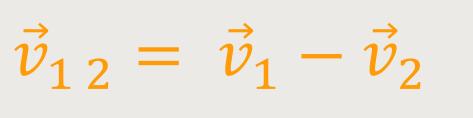
Nach Newton III (Wechselwirkungssatz) ist:

Wenn man beides entsprechend einsetzt, erhält man:

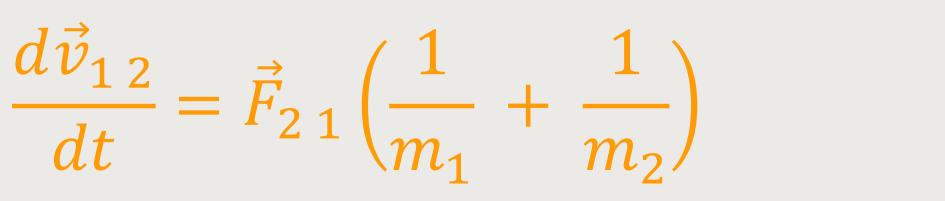
Für 1/m_₁ + 1/m_₂ kann man auch (m_₁ + m_₂ ) / m_₁ · m_₂ schreiben.

Um das weiter zu vereinfachen, setzt man eine reduzierte Masse an:

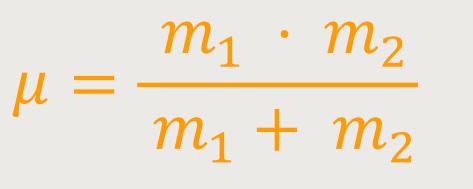
μ   ist die reduzierte Masse

Hinweis:
Hierbei wurden bereits Zähler und Nenner mitein­ander vertauscht, weil sie in der Gleichung auf die andere Seite gebracht werden müssen. Durch Einsetzen der reduzierten Masse erhalten wir nur noch eine Bewegungsgleichung:

Durch diesen formalen Trick gelingt es, ein System mit zwei gekoppelten Differenzial­gleichungen zurück­zuführen auf eine Bewegungs­gleichung. Und diese eine Gleichung beinhaltet sowohl die Relativ­geschwindig­keit als auch die reduzierte Masse.

Das bedeutet nichts anderes, als dass die Relativ­bewegung zweier wechsel­wirkender Massen­punkte m_₁ und m_₂ reduziert wird auf die Bewegung einer reduzierten Masse μ im Feld der Wechsel­wirkungs­kraft _{₁ ₂}.

Und was ist, wenn man mehr als zwei Körper betrachtet? Mehr als zwei Körper kann man analytisch nicht mehr lösen. Das geht nur mit numme­rischen Methoden und ist meistens recht aufwendig. Zumal solche Mehrkörper­probleme nach einiger Zeit Instabili­täten zeigen. Unser Sonnen­system ist demnach ein sehr ausge­klügeltes Mehrkörper­system. Bisher nimmt man an, dass zwischen den verschiedenen Planeten über­wiegend Zweikörper­probleme bestehen. Und diese Zweikörper­probleme sind über Jahrtausende sehr stabil. Wenn man unser Sonnen­system aller­dings mit nummerischen Methoden durchrechnet, zeigen alle Rechen­modelle, dass unser Sonnen­system eigent­lich irgend­wann auseinander­fliegen müsste.

Ich persönlich teile diese Über­zeugung nicht. Wie im Bereich „Neue Physik” gezeigt wird, gibt es durchaus eine Alternative für das Mehrkörper­problem. Das Stichwort heißt Wirbel­strukturen. Doch dazu an anderer Stelle mehr.

Was ist denn, wenn eine Masse sehr groß ist im Verhältnis zu der anderen? Wenn man zum Beispiel das System Sonne-Erde betrachtet? Wenn m_₂ ≠ 0 ist, lässt sich m_₂ wegkürzen und dann erhält man:

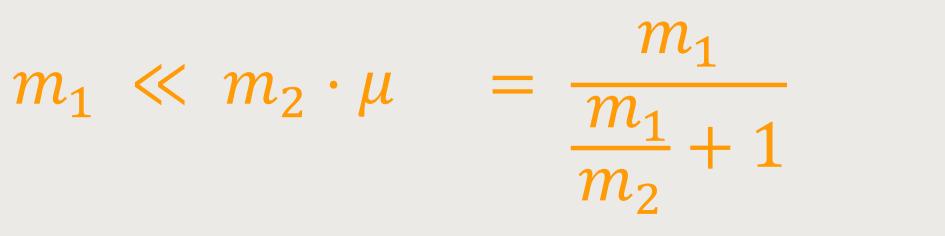
Wenn m_₁ (Erde) sehr klein ist gegen­über m_₂ (Sonne), dann ist m_₁ / m_₂ ∼ 0, und es folgt daraus:

Dadurch lässt sich die Planeten­bewegung in sehr einfacher Weise dar­stellen. Und wenn man alle Planeten mit einbe­zieht, dann taumelt die Sonne nur ein bisschen hin und her. Aber der gemeinsame Schwer­punkt unseres Sonnen­systems liegt trotzdem weiterhin innerhalb der Sonne.

⇦ Kapitel Kapitel ⇨