Bisher haben wir zwei Energieformen besprochen, und zwar die kinetische Energie und die potentielle Energie. Beide haben wir aufgrund des Arbeitsbegriffes eingeführt, weil es in beiden Fällen um eine verrichtete Arbeit ging. Im ersten Fall um eine Arbeit, die man an einem Körper schon verrichtet „hat”. Im zweiten Fall um eine Arbeit, die eine Kraft an einem Körper potentiell verrichten „kann”. Wenn sie also noch verrichtet werden kann, dann ist die Arbeit im Körper gespeichert und abrufbar. Darin besteht also der wesentliche Unterschied. Entweder Arbeit unmittelbar zuführen und wieder abführen, was bei einer negativen Kraft der Fall wäre. Oder Arbeit zuführen und zu irgendeinem späteren Zeitpunkt wieder abrufen. Das ist auch der grundsätzliche Unterschied zwischen Arbeit und Energie.
Wir haben im vorherigen Kapitel die kinetische Energie eingeführt. Das ist ein Parameter, der beschreibt, wie viel Arbeit einem Körper zugeführt werden muss, um ihn aus einem anfänglichen Zustand der Ruhe auf eine bestimmte Geschwindigkeit zu beschleunigen. Wie wir gesehen haben, kann man diese Arbeit sehr allgemein ausdrücken.
Für die kinetische Energie hatten wir erhalten:
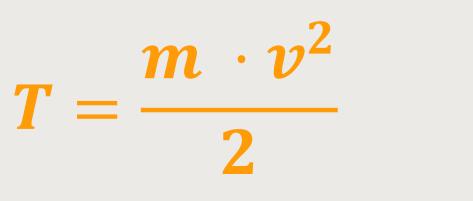
Anschließend hatten wir den zweiten Term dieser Energie, die sogenannte potentielle Energie eingeführt. Wir sind davon ausgegangen, dass sich ein Körper in einem Kraftfeld befindet, wie zum Beispiel dem Gravitationsfeld der Erde oder die Planeten im Gravitationsfeld der Sonne. Das Gleiche trifft auch auf eine Ladung im elektrischen Feld zwischen zwei Kondensatorplatten zu.
Bei unserer Betrachtung haben wir allerdings eine wichtige Einschränkung gemacht. Dieses Kraftfeld muss „konservativ” sein. Das bedeutet, dass sich ein Körper in einem Kraftfeld längs einer geschlossenen Bahnkurve bewegt, vom Anfangspunkt weg, einmal herum, wieder zum Ausgangspunkt zurück. Egal wo sich der Körper gerade befindet, die Summe der zugeführten und wieder abgeführten Arbeit wird stets Null sein. Es wird also längs einer geschlossenen Bahnkurve keine Arbeit verrichtet. Das ist eine Eigenschaft, die man wie bereits erwähnt bei verschiedenen Kraftfeldern vorfindet.
Unter dieser Maßgabe, dass wir uns zunächst auf konservative Kräfte beschränken, ist die potentielle Energie, die ein Körper in einem solchen Kraftfeld hat, die Arbeit, die das Kraftfeld an dem Körper verrichten kann.
Hierbei befindet sich der Körper an einem bestimmten Punkt, bezüglich eines festgelegten Bezugspunktes P₀, und er könnte sich potentiell von dort, wo er ist, zu diesem Bezugspunkt hinbewegen. Er muss es aber nicht, er kann ja auch dort stehenbleiben. In diesem Fall wird die Arbeit zunächst nicht verrichtet. Trotzdem spricht man davon, dass diesem Körper seine Arbeit zugeeignet wurde, sprich seine potentielle Energie.
Sobald er sich jedoch auf den Bezugspunkt P₀ zubewegt, wird die Kraft des Kraftfeldes an ihm Arbeit verrichten. Und damit diese potentielle Energie eindeutig definiert ist, darf sie nicht abhängig sein vom konkreten Verlauf der Bahnkurve. Egal, wie man die Bahnkurve wählt, die Arbeit wird immer die gleiche sein. Und das ist eben nur dann der Fall, wenn man es mit konservativen Kräften zu tun hat.
Hier nochmals die Formel für die potentielle Energie:

Also, bei der potentiellen Energie hängt es immer davon ab, was für ein Kraftfeld man betrachtet.
Im vorherigen Kapitel haben wir bereits gesehen, wie man die Arbeit zwischen zwei Punkten
ausrechnen kann. Indem man die Arbeit am Weg von
Dadurch hatten wir als Ergebnis erhalten, dass die Arbeit gleich der Differenz der kinetische Energien ist:
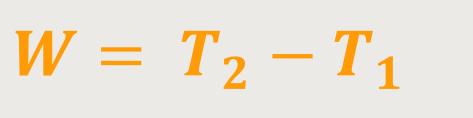
Das ist die Arbeit, die verrichtet wird, wenn sich der Körper vom Punkt
Jetzt wollen wir in ähnlicher Weise ausrechnen, ob man diese Arbeit auch ausdrücken kann mit Hilfe der potentiellen Energie. Hier betrachtet man wieder die Arbeit längs eines Weges von P₁ → P₂.
Man beschreibt im ersten Schritt die Arbeit, wie wir sie bereits definiert haben zunächst
auf. Die Arbeit ist ja das Integral
 ·
d
·
d
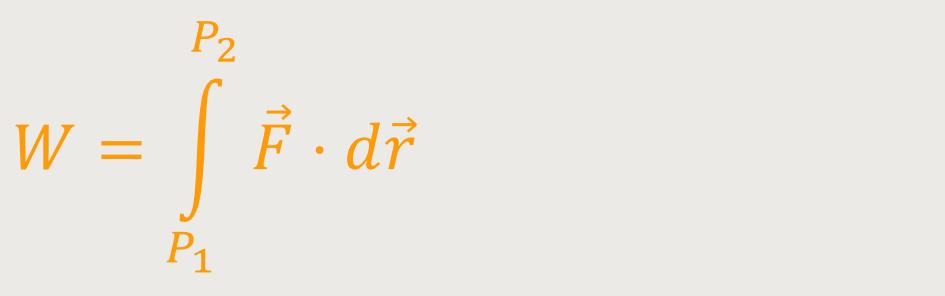
Wir betrachten das Ganze immer noch unter der Voraussetzung, dass wir es mit konservativen Kräften zu tun haben und dass man zudem irgendwo einen Bezugspunkt P₀ festgelegt hat. Hierzu vergleicht man zwei Bahnkurven miteinander. Im ersten Fall bewegt sich der Körper auf der Bahnkurve von P₁ nach P₂. Im zweiten Fall denkt man sich eine Bahnkurve, die von P₁ über den Bezugspunkt P₀ nach P₂ verläuft. Hier wird also der Bezugspunkt P₀ in die Bahnkurve mit einbezogen. In beiden Fällen wird die gleiche Arbeit verrichtet. Und in beiden Fällen ist die Arbeit rundherum gleich Null. Das ist eine Voraussetzung für die konservativen Kräfte.
Das heißt, man kann die Arbeit im zweiten Fall wie folgt beschreiben:
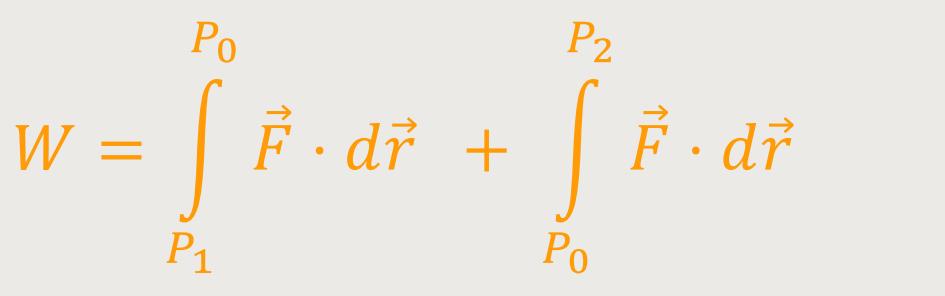
 ist nach wie vor die Kraft in diesem
Kraftfeld. Jedem Raumpunkt ist hier ein entsprechender Kraftvektor
zugeordnet. Im Gravitationsfeld der Erde wäre das an jeder Stelle der gleiche
Kraftvektor dieses homogenen Feldes. Es braucht aber nicht zwingend ein homogenes Feld zu
sein. Es muss nur die Eigenschaft ausweisen, dass die Arbeit wegunabhängig ist.
ist nach wie vor die Kraft in diesem
Kraftfeld. Jedem Raumpunkt ist hier ein entsprechender Kraftvektor
zugeordnet. Im Gravitationsfeld der Erde wäre das an jeder Stelle der gleiche
Kraftvektor dieses homogenen Feldes. Es braucht aber nicht zwingend ein homogenes Feld zu
sein. Es muss nur die Eigenschaft ausweisen, dass die Arbeit wegunabhängig ist.
Hier erhält man ein Integral von

Das ist nichts anderes als die potentielle Energie an der Stelle
Andererseits haben wir ein Integral von

Und das ist nichts anderes als die potentielle Energie an der Stelle
Damit können wir die Arbeit wie folgt ausdrücken:
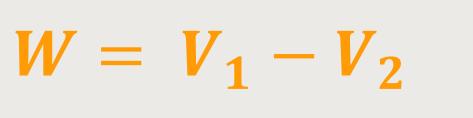
Das ist die Arbeit, die das Kraftfeld verrichtet, wenn sich der Körper vom Punkt P₁ zum Punkt P₂ bewegt. Man kann ohne weiteres erkennen, dass die beiden Ausdrücke für die Arbeit eine gewisse Ähnlichkeit aufweisen.
Wir werden jetzt betrachten, wie die potentielle Energie V und
das Kraftfeld  miteinander
zusammenhängen. Das ist eine besonders wichtige Abhängigkeit, die zeigen wird,
warum in der Physik hauptsächlich die potentielle Energie eine so große
Bedeutung hat.
miteinander
zusammenhängen. Das ist eine besonders wichtige Abhängigkeit, die zeigen wird,
warum in der Physik hauptsächlich die potentielle Energie eine so große
Bedeutung hat.
Um den Zusammenhang erkennen zu können, wollen wir mit einer einfachen Ableitung den
Bezug herleiten. Und zwar unter der Voraussetzung, dass wir zwei Punkte
P₁ und
P₂ untersuchen, die nahe beisammen
sind. Nahe soll in diesem Fall heißen, dass sich über die Distanz zwischen diesen
beiden Punkten die Kraft des Kraftfeldes
 nur wenig ändert, woraus folgt:
nur wenig ändert, woraus folgt:
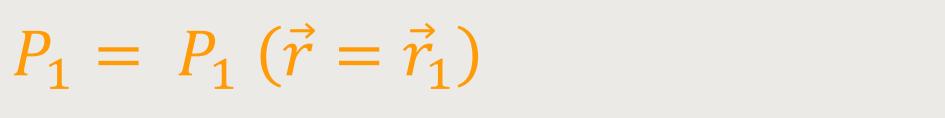
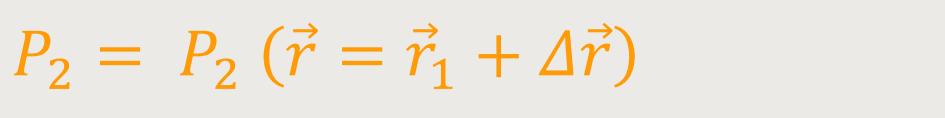
Und jetzt rechnen wir uns die Arbeit aus, welche die Kraft
 längs des Weges von
längs des Weges von
Das werden wir auf zweierlei Weise tun. Einmal mit dem Arbeitsbegriff und einmal mit der Beziehung, die wir erhielten, als wir die Arbeit aus den potentiellen Energien hergeleitet haben.
Zunächst einmal ist die Arbeit als Integral:
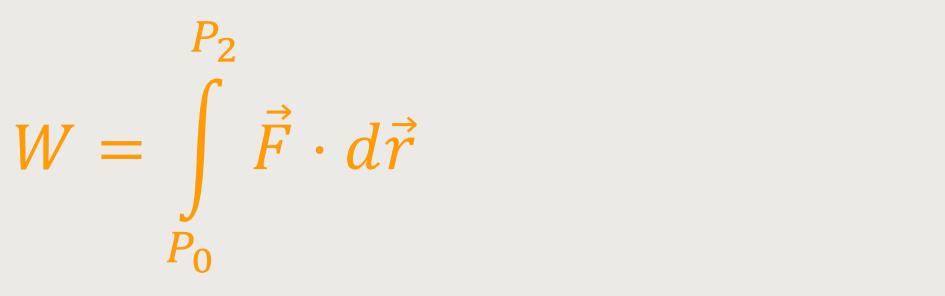
Wenn aber die beiden Punkte P₁ und
P₂ so nahe beieinander liegen, dass
sich das Kraftfeld  praktisch nicht
ändert, dann kann man in guter Näherung die Kraft
praktisch nicht
ändert, dann kann man in guter Näherung die Kraft
 als Konstante vor das Integral setzen
und damit bleibt nur noch stehen:
als Konstante vor das Integral setzen
und damit bleibt nur noch stehen:

Oder anders gesagt, die Kurve ist zwischen den Punkten so kurz, dass man für die Ermittlung dieses Kurvenintegrals die Kurve nicht in noch kleinere Abschnitte unterteilen muss. Die Teilstrecke ist bereits klein genug, um sie ohne große Ungenauigkeit darstellen zu können.
Andererseits können wir diese Arbeit aber auch definieren als:
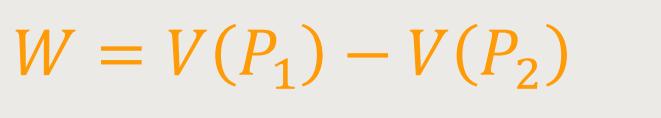
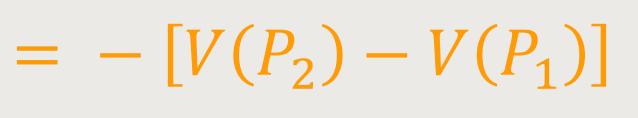
Das lässt sich jetzt umformen. Es geht nämlich um die Differenz von Potentialwerten an nahe beisammen liegenden Punkten:
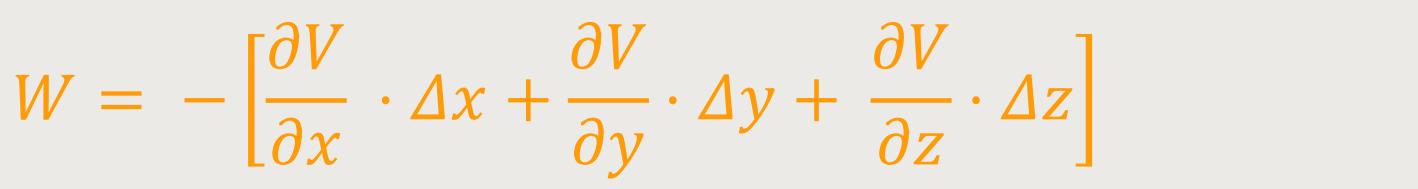
Das ist nur eine einfache Verallgemeinerung einer
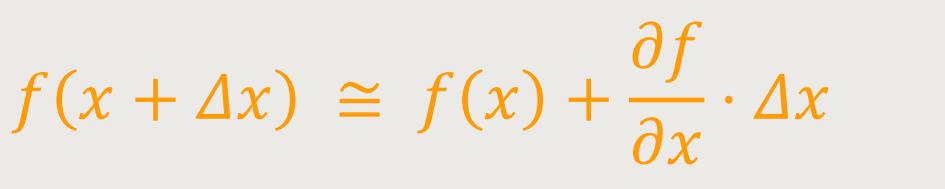
Man ersetzt also die Funktion durch die Tangente und geht um dieses Δx weiter, woraus dann folgt:
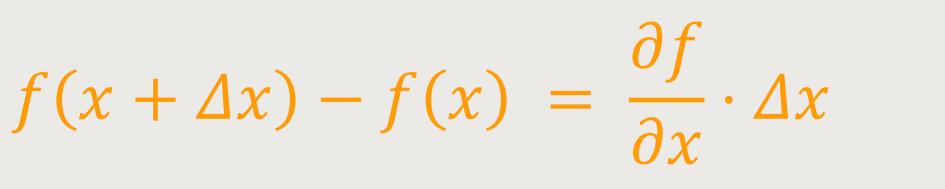
Jetzt stellt sich die Frage, wie lässt sich das darstellen? Dazu führt man den
Gradienten ein. Der Gradient einer skalaren Funktion V ist ein Vektor
mit den Komponenten
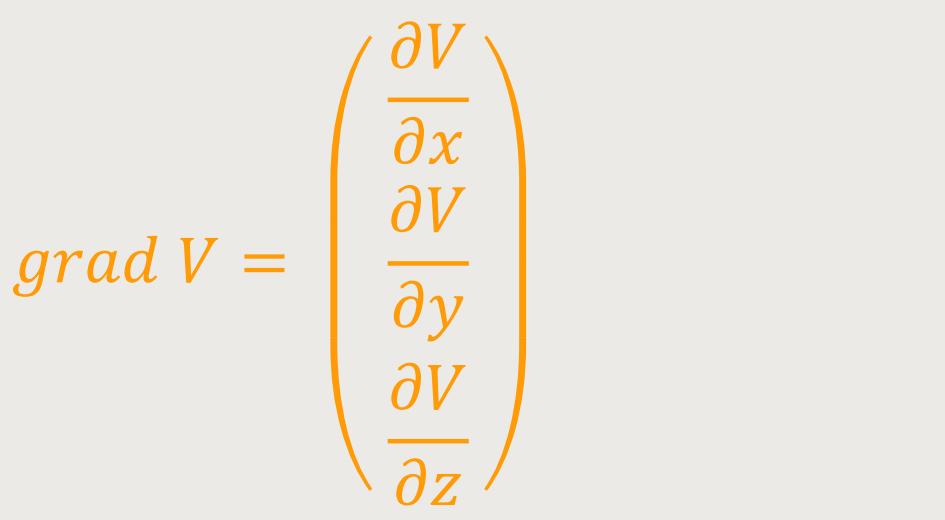
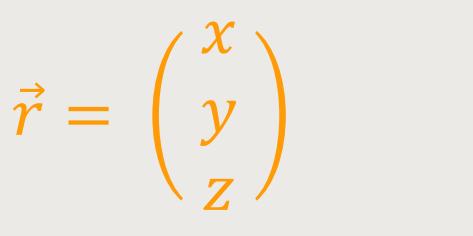
Und das Δ ist die Differenz der beiden Koordinaten der beiden Punkte
P₁ und
P₂:
ist die Differenz der beiden Koordinaten der beiden Punkte
P₁ und
P₂:
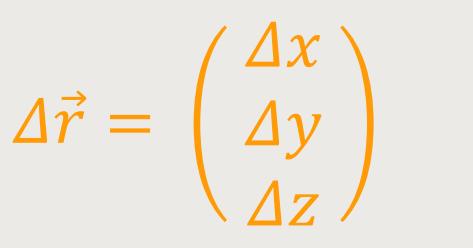
Mithilfe dieser Ausdrücke ergibt sich daraus:

Wenn man jetzt nochmals beide Ausdrücke für die Arbeit miteinander vergleicht, ergibt sich schließlich die Folgerung:

Das ist eine besonders wichtige Beziehung. Denn dadurch wird der Zusammenhang zwischen dem Kraftfeld und der potentiellen Energie in diesem Kraftfeld deutlich.
Wesentlich dabei ist besonders der Umstand, dass es auf die Art und Weise möglich ist, ein Kraftfeld (Vektorfeld) mithilfe nur einer skalaren Ortsfunktion darzustellen. Und auch hier nochmals der Hinweis, das Ganze gilt nur für konservative Kräfte. Bei einem „wirbelhaften” Feld geht so etwas zum Beispiel nicht.
Diese potentielle Energie ist nur dann eindeutig, wenn man einen festen Bezugspunkt P₀ vorgibt. Wechselt man den Bezugspunkt, indem man auf einen anderen Bezugspunkt übergeht, dann wird sich die potentielle Energie nur um einen konstanten Summanden, der auch negativ sein kann, verändern. Wenn man sich im Bezugspunkt P₀ befindet, wird die potentielle Energie Null sein.
Halten wir fest, man kann konservative Kraftfelder als negativen Gradienten der potentiellen Energie schreiben.
Jetzt wollen noch einen Ausdruck für die potentielle Energie ableiten. Das Ganze bezieht sich aber nur auf einen Spezialfall eines „homogenen Kraftfeldes”. Als homogenes Kraftfeld denken wir uns das Kraftfeld der Gravitationskraft auf der Erdoberfläche. An allen Punkten hat die Kraft auf einen Körper den gleichen Betrag. Also, bei einem homogenen Kraftfeld ist der Kraftvektor nicht vom Raumpunkt abhängig.
Der Ortsvektor ist in diesem Fall:
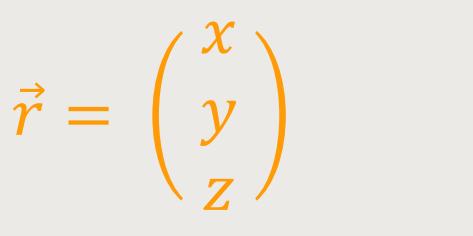
Den Bezugspunkt legt man in den Koordinatenursprung:
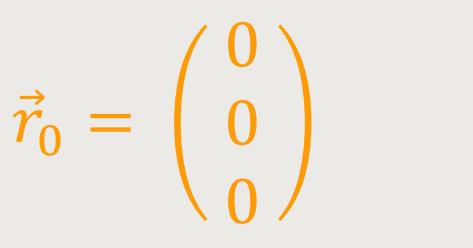
Und die Kraft in diesem homogenen Kraftfeld ist eine konstante Kraft, die
überall nach unten gerichtet ist. Die
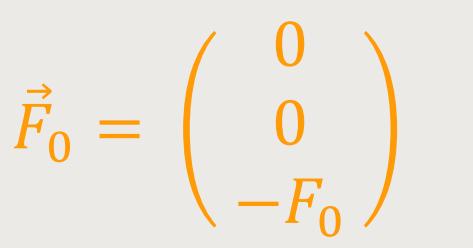
Die Geschwindigkeit an einem beliebigen Punkt stellt sich wie folgt dar:
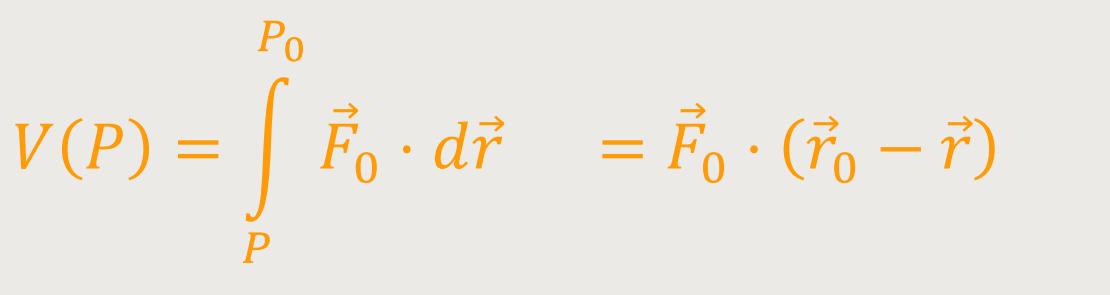
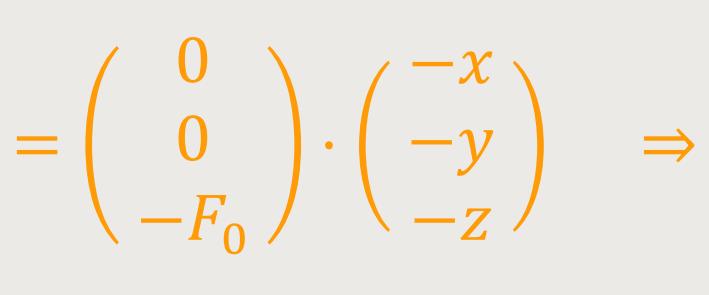
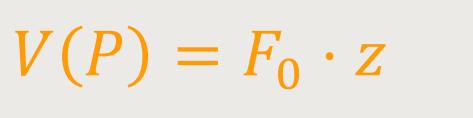
Wenn man sich also in einem homogenen Kraftfeld befindet, und die
Hinweis:
Dieses F₀ ist gleich
Obige Ableitung ist nur ein Ausdruck für einen „Spezialfall” im homogenen Kraftfeld!
Dagegen ist die Beziehung
Nachdem wir jetzt beide Arten der Energie behandelt haben, können wir die Ergebnisse zusammenfassen. Die mechanische Gesamtenergie ist demnach:
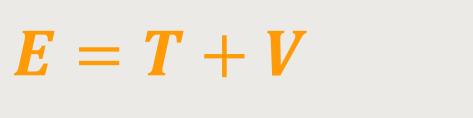
Man misst einem Körper (einem Teilchen oder Massenpunkt) eine „kinetische” Energie und eine „potentielle” Energie zu. Die Summe der beiden ist dementsprechend seine Gesamtenergie. Diese Größe führt zu einem ganz wichtigen Erhaltungssatz. Nämlich dem Energieerhaltungssatz (s.u.).
Denn wir können uns jetzt die Arbeit ausrechnen vom Punkt P₁ → P₂ (s.o.):
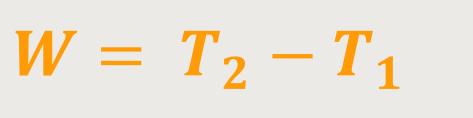
Also die Differenz der kinetischen Energien zwischen Endpunkt und Anfangspunkt.
Quasi, wie viel man an Arbeit noch hineinstecken muss.
Andererseits haben wir die Arbeit auch wie folgt hergeleitet:
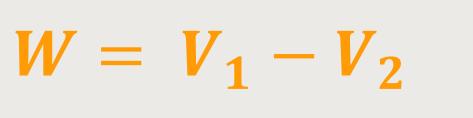
Daraus ergibt sich schlussendlich:
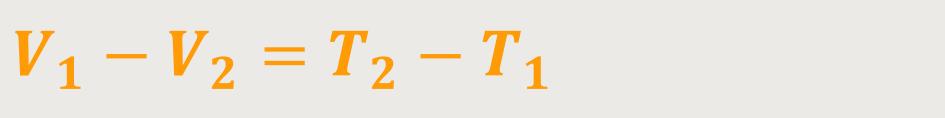
Und daraus lässt sich der „Energieerhaltungssatz” ableiten:
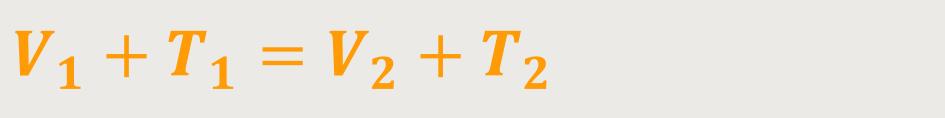
Dieser Satz gilt allerdings nur für konservative Kräfte, und er besagt:
In einem System mit konservativen Kräften bleibt die mechanische Gesamtenergie konstant.
Dennoch kann man durch Hinzunahme von thermischer Energie den Gültigkeitsbereich dieses Erhaltungssatzes erweitern. Diese Erweiterung des Energiesatzes auf den Bereich, wo auch thermische Energien mit berücksichtigt werden, führt dann zum Ersten Hauptsatz der Thermodynamik.
Der Geltungsbereich des Impulserhaltungssatzes dagegen gilt allgemeiner als der Energieerhaltungssatz, weil er nicht auf konservative Kräfte beschränkt ist.
Sehr schön lässt sich das an einem Pendel illustrieren. Bei einem Pendel gibt es ständig einen Wechsel zwischen potentieller Energie und kinetischer Energie. Und die Summe der beiden, bleibt entsprechend dem Energieerhaltungssatz, stets konstant. Es schwingt also gewissermaßen die Energie zwischen kinetischer und potentieller Energie hin und her.
Dazu kommen wir im übernächsten Kapitel.
⇦ Kapitel Kapitel ⇨
