Der Drehimpuls spielt bei der „Punkt­mechanik” keine große Rolle. Der Grund dafür besteht darin, dass Massen­punkte oder Teilchen definitions­gemäß nach bisherigem Verständnis Gebilde sind, die keine signi­fikante innere Struktur aufweisen. Und daher kann ein Massen­punkt auch nicht rotieren. Wenn es also um „Rotations­bewegungen” geht, betrachten wir hier primär ausgedehnte Körper.

Was für einzelne Teilchen gilt, trifft natürlich auch auf Systeme von Massen­punkten zu. Das ist insbesondere dann wichtig, wenn diese Schluss­folgerung auf makros­kopische Körper über­tragen werden soll. Selbst ein starrer Köper ist auch nichts anderes als ein System von Massen­punkten.

In der Natur sind oft „Zentral­kräfte” wichtig. Das sind Kräfte, die sich an einem „Kraft­zentrum” orientieren. Für die weitere Betrachtung wird in dieses Zentrum der Koordinatenur­sprung gelegt. In einem solchen Kraftfeld liegt der Kraft­vektor immer parallel zum Orts­vektor || . In diesem Fall gilt, dass das Drehmoment immer gleich Null ist, und damit bleibt der Dreh­impuls erhalten:

Voraussetzung ist allerdings, dass es sich um ein Zentral­kräfte­feld handelt. Nur so bleibt zum Beispiel bei der Bewegung der Erde um die Sonne der Dreh­impuls erhalten. Mit anderen Worten, der Entfernungs­radius von der Sonne zur Erde, also der Radius­vektor, überschreitet in gleichen Zeiten gleiche Flächen.

Der „3. Erhaltungs­satz”, den wir jetzt näher betrachten wollen, bezieht sich ausschließ­lich auf ein System von Massen­punkten. Denn um kompli­zierte Bewegungen von vielen Massen­punkten irgendwie beschreiben zu können, führt man sinnvoller Weise eine zusätzliche Größe ein – den „Massen­mittelpunkt”. Dadurch ist es möglich, gewisse Aspekte heraus­zugreifen, die dann wieder in einen Erhaltungs­satz münden. Der Massen­mittel­punkt ist ein Punkt, dem ein System von Massen­punkten zugeordnet wird.

Der Ortsvektor des Massen­mittel­punktes wird wie folgt definiert:

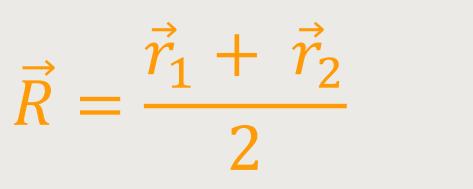
Der Massen­mittel­punkt ist sozusagen der arith­metische Mittel­wert der Orts­vektoren der jeweiligen Massen­punkte. Wenn die Massen­punkte nicht gleich groß sind, führt man eine Gewichtung ein. Ein solch gewichteter Mittel­wert mit den einzelnen Massen ergibt sich aus:

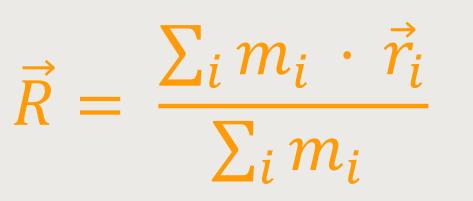
Das ist die allgemeine Definition des Massen­mittel­punktes.

Das hat aber „nichts” mit einem Gewicht zu tun und auch „nichts” mit der Schwer­kraft. Für den Begriff Massen­mittel­punkt sagt man auch gerne „Schwer­punkt”. Die Wolke von Massen­punkten wird somit durch einen Massen­mittelpunkt charakte­risiert, der irgendwo mittendrin liegt und möglichst nahe bei den meisten Einzel­massen. Jetzt wollen wir heraus­finden, wie sich dieser Massen­mittelpunkt bewegen wird. Und was passiert insbesondere mit dem Impuls dieses Massen­mittel­punktes?

Im ersten Moment würde man denken, der Massen­mittelpunkt kann doch gar keinen Impuls haben, weil er keine Masse hat. Er ist doch nur ein „gedachter” Punkt. Dennoch lässt sich diesem Massen­mittelpunkt sinnvollerweise eine Masse zuordnen. Hierzu denkt man sich die gesamte Masse des Systems in einem „einzigen” Massen­mittelpunkt vereinigt. Anschließend über­legt man sich, was mit dem Impuls dieses Massen­mittel­punktes im Laufe der Zeit passieren wird.

Um das weiter untersuchen zu können, wird obige Gleichung weiter umgeformt.

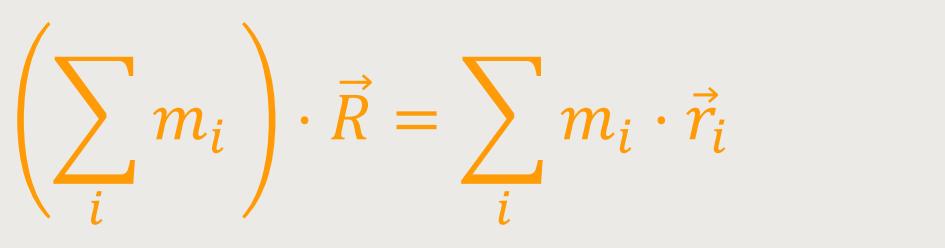
Σ_i m_i   entspricht der Masse aller Massen­punkte
     ist der Orts­vektor des Massen­mittel­punktes

Dann differenzieren wir nach der Zeit:

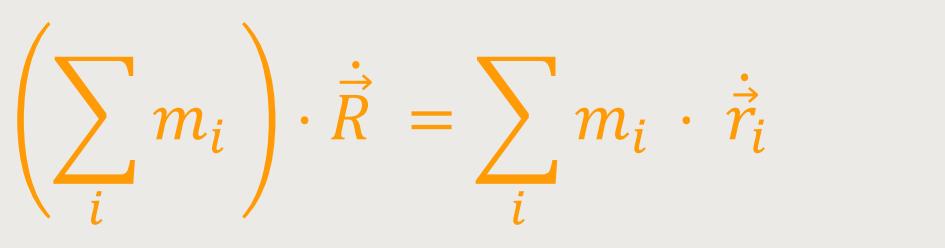
Und jetzt differenzieren wir noch einmal nach der Zeit, wobei m_i · _i = _i entspricht:

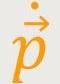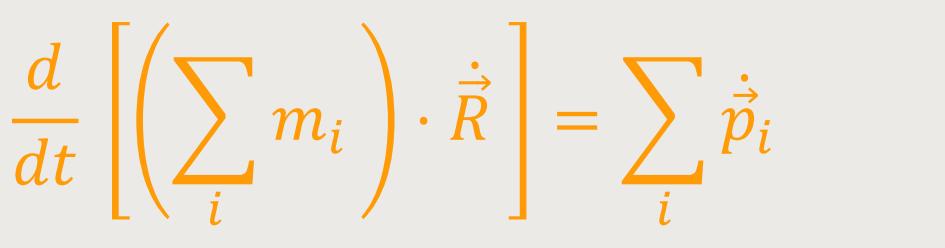
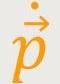_i   sind die Kräfte, die auf die Teilchen angreifen

Es gibt prinzipiell zwei Arten von Kräften, die an so einem Teilchen angreifen können. Einmal eine „äußere” Kraft, wie zum Beispiel die „Gravitations­kraft”. Und als zweites gibt es mögliche „Wechsel­wirkungs­kräfte” zwischen den Teilchen. Bevor man über alle Kräfte bei allen Teilchen aufsummiert, sollte man eine wichtige Überlegung mit einbeziehen. Denn überall dort, wo gleich große Wechsel­wirkungs­kräfte vorliegen, lassen sich diese „inneren” Kräfte paarweise wegkompen­sieren. Was übrig bleibt, sind dann letztlich nur die „äußeren” Kräfte.

Σ_i entspricht Σ_{i i} woraus folgt:

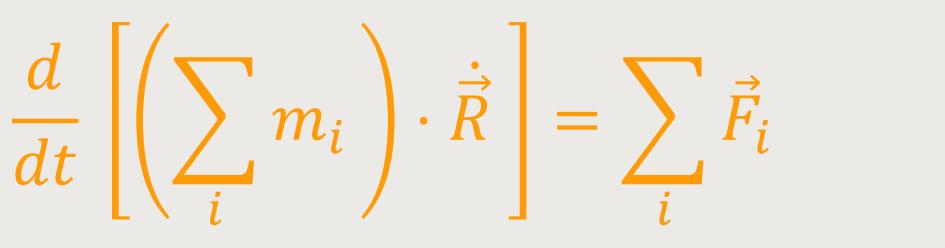
Wir erhalten damit den Erhaltungs­satz des Massen­mittel­punkt­impulses. Dieser Satz wird auch gern als „Schwerpunkt­satz” bezeichnet.

Wenn die gesamte äußere Kraft verschwindet (Σ_{i i} = 0), bleibt der Impuls der im Massen­mittel­punkt vereinigt gedachten gesamten Masse des Systems konstant.

Wenn man jetzt differenziert, ergibt sich folgendes:

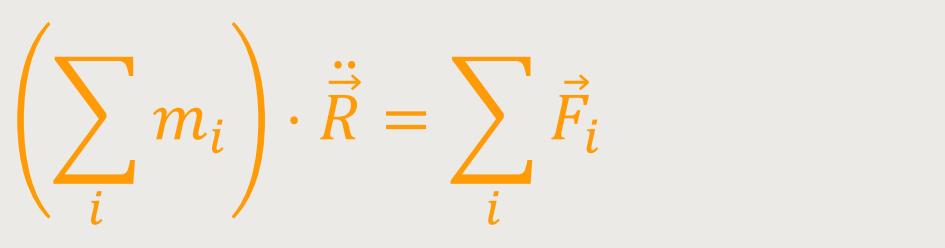
Σ_{i i}   ist wieder die gesamte äußere Kraft

  ist die Beschleunigung des Massen­mittel­punktes

Das ist nichts anderes als das 2. Newton-Axiom umgesetzt auf den Massen­mittelpunkt.

Daraus lässt sich folgendes schluss­folgern: Der Massen­mittel­punkt des Systems bewegt sich so, wie wenn die gesamte äußere Kraft an der gesamten Masse des Systems, die im Massen­mittel­punkt vereinigt gedacht wird, angreifen würde.

Bisher haben wir drei Größen kennen­gelernt, die erhalten bleiben. Der „Impuls”, der „Dreh­impuls” und der „Massen­mittelpunkt”. Alle drei Größen sind jeweils durch drei Komponenten (Vektoren) bestimmt, in Summe ergeben dies neun Vektoren.

Es gibt noch eine weitere Größe, und zwar eine „skalare” Größe, die unter gewissen Voraus­setzungen auch zeit­unabhängig bleibt und daher erhalten ist. Hierbei handelt es sich um die „Energie”. Zunächst sprechen wir über die mechanische Energie. Doch bevor wir darauf eingehen, müssen wir noch zwei andere Begriffe erläutern. Den Begriff der „Arbeit” und der „Leistung”. Das sind zunächst einmal nur Definitionen. Aber anschließend können wir daraus sehr wichtige Schluss­folgerungen ziehen.

⇦ Kapitel Kapitel ⇨