Bisher ging es in der Kinematik um die Leere von den Bewegungen, also um die Frage, was ist die Ursache für diese Bewegungen. In diesem Bereich geht es jetzt insbesondere um Geschwindig­keiten und Beschleuni­gungen. Und die „Dynamik” beschäftigt sich mit der Frage nach dieser Ursache.

Bei näherer Betrachtung stellt sich heraus, dass für die Bewegungen und die Beschleuni­gungen Kräfte angenommen werden können, die auf die betrachteten „Massen­punkte” wirken. Das bedeutet, dass der Bewegungs­ablauf eines Massen­punktes beeinflusst wird durch Wechsel­wirkungen mit der Umgebung. Demnach müssen diese Wechsel­wirkungs­kräfte eine gewisse Reichweite haben.

Da gibt es einer­seits sehr lange Reich­weiten bis hin zu unend­licher Reich­weite. Bisher geht man davon aus, dass dies bei der „Gravitations­kraft” der Fall ist. Aber auch die elektro­magnetische Kraft ist eine solche unendlich weit­reichende Kraft. Daneben gibt es noch zwei weitere Kräfte. Die starke und die schwache Wechsel­wirkung. Diese haben allerdings extrem kurze Reichweiten. Wobei die Reichweite der starken Wechsel­wirkung auf den Bereich der Atomkerne beschränkt ist. Insbesondere die Kräfte mit kurzer Reichweite sind so beschaffen, dass sie bereits im Bereich der Atom­hülle, wo sich die Elektronen befinden, die starke Wechsel­wirkung gar nicht mehr spüren.

Der erste, der das erkannt hat, war Newton. Deshalb wird die „Kraft­einheit” auch nach ihm benannt. Er hat nämlich erkannt, dass der Begriff der Kraft physikalisch gesehen ein zentraler Begriff ist der uns hilft, die Dinge zu interpretieren. Um mit dieser Kraft entsprechend umzugehen, und mit Hilfe des Kraft­begriffes die Mechanik aufbauen zu können, benötigt man gewisse Grund­gesetze. Diese Gesetze werden im Bereich der klassischen Mechanik als „Axiome” bezeichnet. Genauer gesagt als die „Newton'schen Axiome”. Eigentlich kommt dieser Begriff aus der Mathematik. Ein Axiom ist ein nicht weiter beweisbarer Satz, den man annimmt und aus welchem dann weitere Folgerungen gezogen werden.

Man legt also gewisse „Sätze” einfach zugrunde, auch wenn sie zunächst nicht beweisbar sind. Entscheidend ist allerdings, dass die sich daraus ergebenden Schluss­folgerungen mit der Erfahrung zusammen­passen. Dieses Vorgehen ist in anderen Bereichen der Physik ebenfalls sehr wichtig, etwa in der Elektro­dynamik. Dort gibt es auch solche Grund­gleichungen, auf denen die Elektro­dynamik aufbaut. Das sind die schon mehrfach erwähnten Maxwell-Gleichungen.

Halten wir zunächst fest: Wir können die Kräfte als Ursache von Beschleuni­gungen eines Körpers ansehen. Das heißt im Umkehr­schluss, wenn keine Kraft wirkt, gibt es keine Beschleunigung.

Das dem so ist, besagt das 1. Newton-Axiom. Man bezeichnet es auch als „Trägheits­satz”.

Ein kräfte­freier Körper, auf den keine Kraft wirkt, bleibt entweder in Ruhe oder in gleichförmiger geradliniger Bewegung, also unbeschleunigt.

Das bezieht sich allerdings nicht auf jedes Bezugs­system. Es trifft nur auf Systeme zu, in denen der Trägheits­satz gilt. Diese Systeme nennt man deshalb auch „Inertial­systeme”.

Letztlich kann man nur in experimen­tellen Unter­suchungen herausfinden, ob ein betrachteter Körper als kräftefrei anzusehen ist.

Hierzu führen wir den Begriff des „Impulses” ein. Den Impuls definiert man wie folgt:

m   Masse des Teilchens
  Geschwindigkeit

Bei der Masse handelt es sich um die „träge” Masse eines Körpers. Daneben wird nämlich in der Physik auch eine zweite Art von Masse betrachtet: Die „schwere” Masse. In zahl­reichen Experimenten mit hoher Präzision hat sich heraus­gestellt, dass diese beiden Arten letztlich immer proportional zueinander sind. Und so hat man sich darauf geeinigt, dass man letztlich nur eine Masse betrachtet. Dennoch ist es äußerst wichtig, diese zwei unter­schied­lichen Begriffe gut auseinander­halten, wie wir noch sehen werden.

In Verbindung mit der Relativitäts­mechanik hat man erstmals verstanden, dass diese beiden Massen immer proportional zueinander sind. Und so kann man sie als „wesensgleich” ansehen.

Das zweite Newton-Axiom bezeichnet man auch als „Aktionssatz”.

Jede Impuls­änderung eines Körpers wird hervor­gerufen durch eine Kraft. Eine Kraft wird angesehen als zeitliche Änderung eines Impulses.

Die zeitliche Änderung des Impulses definiert man wie folgt:

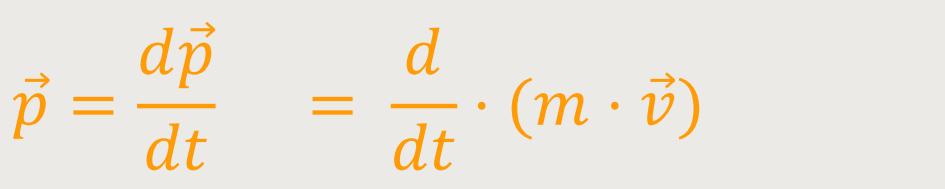
Kräfte werden also angesehen als Ursachen von zeitlichen Änderungen des Impulses. Auch das gilt wieder nur in einem Inertialsystem.

Zur Zeit Newtons ist man davon ausgegangen, dass sich die Masse nicht ändert, wenn sich ein Bewegungs­zustand ändert. Bei der relativis­tischen Mechanik jedoch kann die Masse nicht als unabhängig vom Bewegungs­zustand angesehen werden. Nur für die normalen Geschwindig­keiten unseres Alltags bleibt die Definition erhalten. Aber wenn wir uns der Licht­geschwindig­keit annähern, ändert sich die Physik komplett. Dort kommt es dann zu wesent­lichen Veränderungen der Masse in Zusammen­hang mit den Bewegungs­änderungen. Doch in den aller­meisten Fällen die uns in der klassischen Mechanik interessieren, kann man davon ausgehen, dass es eine konstante Masse gibt.

Falls m = const, lässt sich das 2. Newton-Axiom wie folgt umschreiben:

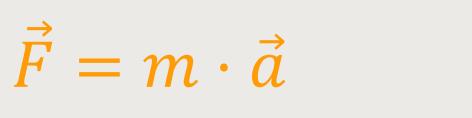
Wenn zum Beispiel eine konstante Kraft auf einen bestimmten Körper mit einer Masse von 1 kg wirkt, dann wird es eine gewisse Beschleuni­gung geben. Wenn jetzt die gleiche unveränderte Kraft auf einen Körper mit einer Masse von 10 kg wirkt, beträgt die Beschleuni­gung nur noch 1 /10.

Also, je größer die Masse des Körpers ist, desto weniger wird er beschleunigt werden. Das bedeutet wiederum, dass dieser Körper sich umso mehr einer Beschleuni­gung seiner selbst widersetzt, je größer seine Masse ist. Man sagt auch, dass er umso „träger” ist. Die Masse m charakte­risiert demnach die Trägheit des Körpers. Daher nennt man m auch die träge Masse.

Wenn man nun eine solche Masse betrachtet, wird sie mit einer gewissen Kraft zur Erde gezogen. Das ist, was man unter dem „Gewicht” eines Körpers versteht, sprich wie stark er zur Erde gezogen wird. Folgendes muss man sich immer vor Augen halten: Das Gewicht ist eine „Kraft”. Die Masse ist ein „Skalar”. Und wenn jetzt der Körper eine größere Masse hat, dann wird dieser auch stärker zur Erde angezogen. Gleich­zeitig wird er aber auch träger. Die Träg­heit, als grund­legende Eigen­schaft eines Körpers mit einer Masse, bleibt bestehen.

Oder wenn wir an die Elektro­statik denken. Entladen (durch Erdung) kann man Körper schon, entmassen (das man ihnen die Schwere wegnimmt) kann man dagegen nicht. Der Unter­schied ist, dass die Masse, die man als „schwere” Masse bezeichnet, dafür verant­wortlich ist, das sich zwei Massen anziehen. Die Anziehung muss zunächst aber noch nichts mit der Trägheit, im Sinne einer Beschleunigungs­möglichkeit, zu tun haben. Die Erfahrung zeigt jedoch, dass diese beiden Dinge immer Hand in Hand gehen. Das ist ein wesentlicher Grund dafür, warum man gerne Masse und Gewicht miteinander verwechselt.

So sagt man oft: "Auf dem Mond hat ein Körper eine kleinere Masse". Das stimmt genau­genommen nicht. Er hat ein kleineres Gewicht, weil er weniger stark angezogen wird. Wir werden bei der Gravitations­kraft später nochmals näher darauf eingehen. Die träge Masse ist also eine Größe, welche die Träg­heit gegen eine Beschleuni­gung charakte­risiert, wogegen die schwere Masse aussagen will, wie stark die Masse von einer anderen Masse angezogen wird. Die „schwere” Masse geht immer Hand in Hand mit der „trägen” Masse.

Ein Spezialfall ist gegeben, wenn eine konstante Kraft _₀ vorliegt. Bei einer konstanten Beschleuni­gung und konstanter Masse ergibt sich daraus:

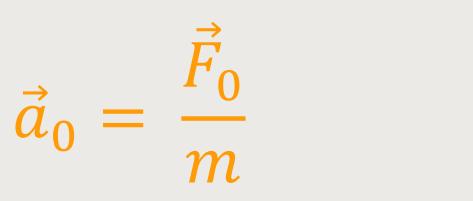
Darunter versteht man auch eine gleich­förmig beschleunigte Bewegung.

Laut Kinematik ergibt sich für die Geschwindigkeit:

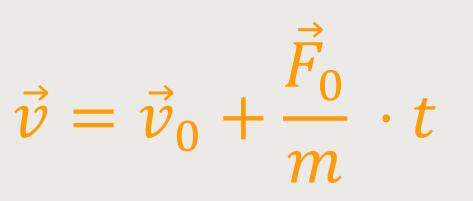
Und für den Ortsvektor gilt:

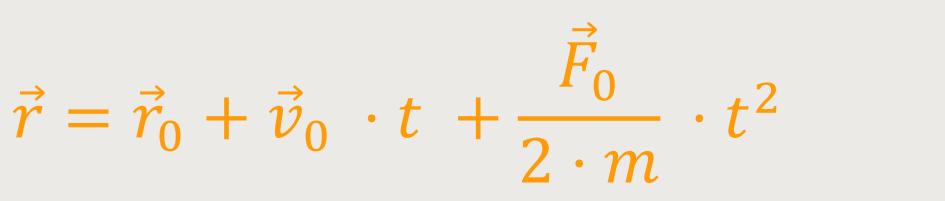
Falls man einen kräfte­freien Körper hat _₀ = , dann ergibt sich daraus für die Geschwindigkeit und den Ortsvektor:

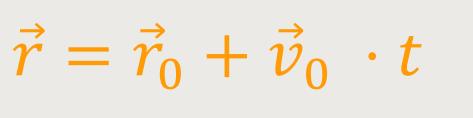
Das ist nichts anderes als eine geradlinig gleich­förmige Bewegung.

⇦ Kapitel Kapitel ⇨