Die „Kreisbewegung” ist weder eine unbeschleunigte, noch eine gleichförmig beschleunigte Bewegung.
Zunächst möchten wir auch hier ein Bezugssystem festlegen. Dazu nehmen wir wieder das kartesische Bezugssystem. Also senkrecht aufeinander stehende Koordinatenachsen (x-y-z). In diesem Fall setzten wir voraus, dass es sich um ein Rechtssystem handelt. Das ist wichtig, weil es nämlich zwei Arten von kartesischen Bezugssystemen gibt. Das „Rechtssystem”, auch Rechte-Hand-Regel genannt, und das „Linkssystem” – Linke-Hand-Regel.
Beide Bezugssysteme sind spiegelbildlich zueinander. Um das zu veranschaulichen, werden der Mittel- und Zeigefinger sowie der Daumen der jeweiligen Hand so gespreizt, dass alle drei Finger einen „rechten Winkel” zueinander beschreiben. Das ist dann gleichbedeutend mit den drei Achsen x-y-z. Der Zeigefinger zeigt jeweils von einem weg, sodass der Daumen nach oben zeigt. Benutzt man dazu beide Hände gleichzeitig, so zeigen die Spitzen der beiden Mittelfinger aufeinander.
Also, das Basiskoordinatensystem für die weitere Betrachtung ist das Rechtssystem. Diese Voraussetzung ist wesentlich, wie wir noch sehen werden. Die Bewegung soll auf einem Kreis erfolgen. Das heißt, es gibt eine „feste Drehachse”, um die sich das betrachtete Teilchen dreht. Der Koordinatenursprung des Bezugssystems liegt ebenfalls auf dieser Drehachse, und ist daher auch unbeschleunigt.
Grafik (wird später eingefügt)
Um anschließend noch die Bewegung eines starren Körpers beschreiben zu können, legen wir den Nullpunkt des Koordinatensystems nicht in den Mittelpunkt des Kreises. Sondern wir legen ihn unterhalb der Kreisfläche in einem verhältnismäßigen Abstand irgendwo auf der Drehachse.
Der Ortsvektor  zeigt jetzt vom
Ursprung O zum Punkt P, wo sich das Teilchen
gerade auf der Kreisbahn befindet. Auf dem Kreis können wir zusätzlich noch
einen Ausgangspunkt P₀ festlegen, von dem aus
sich das Teilchen in Richtung P bewegt. Vom Mittelpunkt des Kreises
aus hat der Radiusvektor R einen Winkel
φ (phi) überstrichen.
zeigt jetzt vom
Ursprung O zum Punkt P, wo sich das Teilchen
gerade auf der Kreisbahn befindet. Auf dem Kreis können wir zusätzlich noch
einen Ausgangspunkt P₀ festlegen, von dem aus
sich das Teilchen in Richtung P bewegt. Vom Mittelpunkt des Kreises
aus hat der Radiusvektor R einen Winkel
φ (phi) überstrichen.
Den Kreisbogen, der vom Teilchen dabei überschritten wird, bezeichnen wir als s. Die Bogenlänge ist demnach:

Der Winkel φ ist hierbei jedoch im Bogenmaß gegeben und nicht als Grad, weil man in der Physik im Allgemeinen so vorgeht. Da der Nullpunkt des Koordinatensystems weiter unten auf der Drehachse liegt, bildet der Radiusvektor R mit dem Ortsvektor ein rechtwinkliges Dreieck. Diesen unteren Winkel nennen wir ϑ (theta).
Der Radius der Kreisbahn lässt sich demnach definieren als:
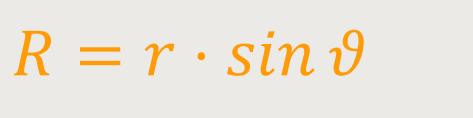

An dieser Stelle ist die Einführung einer weiteren Größe sehr wichtig.
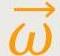
Die „Winkelgeschwindigkeit” hat vektoriellen Charakter, weshalb man sie
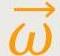 nennt. Die Winkelgeschwindigkeit
definiert man zum einen auf Grundlage des Betrags dieses Vektors.
nennt. Die Winkelgeschwindigkeit
definiert man zum einen auf Grundlage des Betrags dieses Vektors.
Deshalb nennen den Betrag einfach die Winkelgeschwindigkeit. Demnach ist der Betrag:
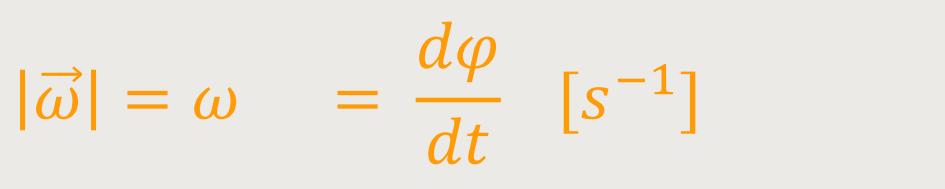
Hier handelt es sich um den Winkel, der von diesem Radiusvektor pro Zeiteinheit überstrichen wird. „Winkel” ist hier eine dimensionslose Größe bzw. [s(-1)]. Halten wir fest: Der Betrag der Winkelgeschwindigkeit ist der Winkel der von dem Radiusvektor pro Zeiteinheit überstrichen wird.
Als Nächstes geben wir die Richtung des Geschwindigkeitsvektors vor.
Der Vektor der Winkelgeschwindigkeit 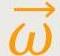 ist parallel zur Drehachse gerichtet. Die Richtung dieses Vektors richtet sich nach der
Umdrehungsrichtung der Kreisbahn. Hierbei einigt man sich auf die
Rechte-Hand-Regel als Richtungssinn. Wenn die Finger der rechten
Hand (leicht geschlossen) in Richtung der Drehbewegung zeigen, dann zeigt der gespreizte Daumen
in Richtung des Winkelgeschwindigkeitsvektors. Mit anderen Worten, er liegt auf
der Drehachse und zeigt vom Kreismittelpunkt nach vorne (oben).
ist parallel zur Drehachse gerichtet. Die Richtung dieses Vektors richtet sich nach der
Umdrehungsrichtung der Kreisbahn. Hierbei einigt man sich auf die
Rechte-Hand-Regel als Richtungssinn. Wenn die Finger der rechten
Hand (leicht geschlossen) in Richtung der Drehbewegung zeigen, dann zeigt der gespreizte Daumen
in Richtung des Winkelgeschwindigkeitsvektors. Mit anderen Worten, er liegt auf
der Drehachse und zeigt vom Kreismittelpunkt nach vorne (oben).
Das ist nicht unerheblich, denn in der „Elektrodynamik” gibt es auch die Rechte-Hand-Regel, bezogen auf die Flussrichtung des Stroms in einer Spule und der Anordnung des Magnetfelds. Der Vektor der magnetischen Flussdichte ist ebenso wie der Winkelgeschwindigkeitsvektor ein Axialvektor, der lediglich die Richtung angibt.
Nun kann man mit Hilfe dieses Winkelgeschwindigkeitsvektors die Geschwindigkeit eines bewegten Teilchens in einer sehr einfachen Weise darstellen.
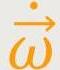
Die Winkelbeschleunigung ist definiert als:
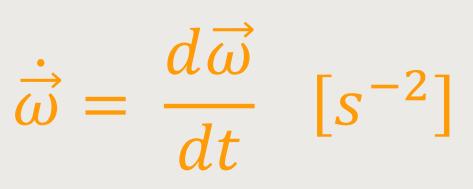
Es geht also um die Änderung der Winkelgeschwindigkeit pro Sekunde und das pro Sekunde, deshalb s(-2).
Der Betrag der Winkelbeschleunigung ist:
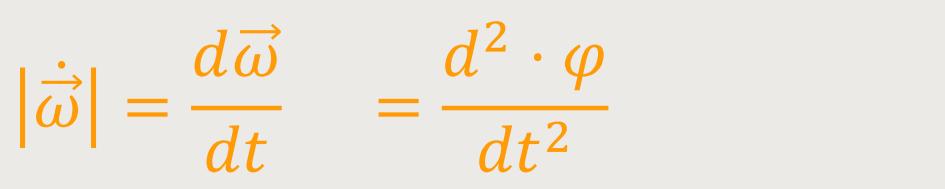
Und da es sich um eine Kreisbewegung handelt, ist die Winkelbeschleunigung parallel
zur Winkelgeschwindigkeit
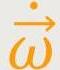 ||
||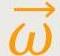
Alles schön und gut, aber das eigentliche Ziel ist es, die Bewegung dieses Teilchens auf
der Kreisbahn zu beschreiben. Deshalb erhält der Punkt (das Teilchen) einen
Geschwindigkeitsvektor  . Da es
sich hierbei um einen Tangentialvektor handelt, ändert dieser ständig seine
Richtung und kann je nach Anwendungsfall auch seine Länge ändern.
. Da es
sich hierbei um einen Tangentialvektor handelt, ändert dieser ständig seine
Richtung und kann je nach Anwendungsfall auch seine Länge ändern.

Den „Geschwindigkeitsvektor” kann man ganz gut in einer übersichtlichen
Form mithilfe des Winkelgeschwindigkeitsvektors beschreiben. Zunächst schauen
wir uns den Betrag | |
an. Das ist nichts anderes als die Änderung der Wegstrecke mit der Zeit
[m · s-1]:
|
an. Das ist nichts anderes als die Änderung der Wegstrecke mit der Zeit
[m · s-1]:
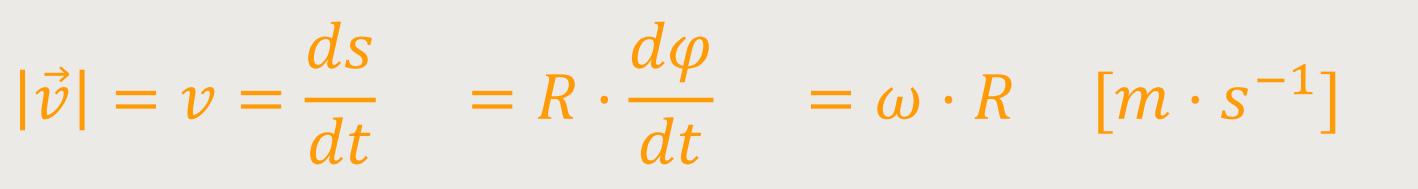
Also, mit mithilfe der Winkelgeschwindigkeit kann man bei bekanntem Kreisradius die Bahngeschwindigkeit, das heißt den Betrag der Geschwindigkeit des Massenpunktes ausrechnen. Nun lässt sich ein Bezug mit der vektoriellen Darstellung der Winkelgeschwindigkeit herstellen. Und zwar, wenn man das Ganze vektoriell schreibt. Dann erhält man ein vektorielles (Kreuz)Produkt:

Aber das darf man nicht verwechseln mit dem Operationszeichen einer Produktrechnung. Denn das vektorielle Produkt zweiter Vektoren ist seinerseits ebenfalls ein Vektor, welches senkrecht auf den einen und senkrecht auf den anderen steht.
Und die Länge des Geschwindigkeitsvektors
 ist gleich der Fläche des von
ist gleich der Fläche des von
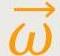 und
und
 aufgespannten Parallelogramms.
Für das vektorielle Produkt gilt, dass sich die Orientierung des Produktvektors
nach der Orientierung des Koordinatensystems richtet. Für den Betrag gilt:
aufgespannten Parallelogramms.
Für das vektorielle Produkt gilt, dass sich die Orientierung des Produktvektors
nach der Orientierung des Koordinatensystems richtet. Für den Betrag gilt:

Selbst wenn sich die Winkelgeschwindigkeit nicht ändert, haben wir mit einer Beschleunigung zu rechnen, weil sich der Geschwindigkeitsvektor ständig ändert. Schließlich ist die Beschleunigung die Änderung des Geschwindigkeitsvektors pro Zeiteinheit.
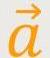
Der Beschleunigungsvektor 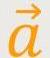 wird wie
folgt definiert:
wird wie
folgt definiert:
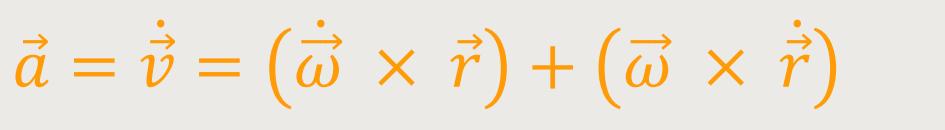

Alternativ kann man auch schreiben:
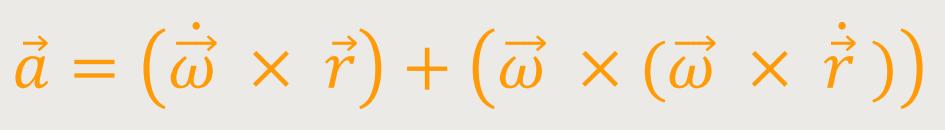
Hinweis: Beim Differenzieren eines vektoriellen Produktes muss man die Produktregel beachten.
Achtung: Das vektorielle Produkt hat die wichtige Eigenschaft, dass es nicht wie das Skalarprodukt kommutativ ist, sondern dass es antikommutativ ist. Würde man die beiden Faktoren vertauschen, würde der Vektor in die andere Richtung schauen. Insofern muss man auf die Reihenfolge der Produkte achten.
Was hat der erste Term bei obigem Vektorprodukt für eine Bedeutung?
Als erstes interessiert uns der Betrag:
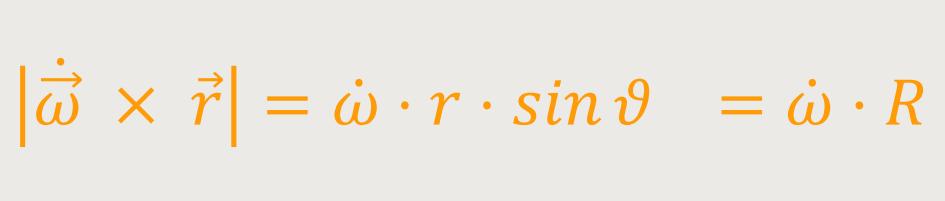
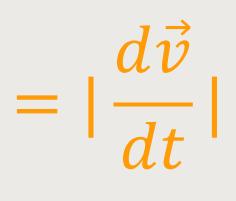
Das ist nichts anderes als der Betrag des Geschwindigkeitsvektors.
Daraus ergibt sich:

Das bedeutet wiederum, dass der erste Term die „Tangentialbeschleunigung”
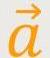 t ist.
t ist.
Schauen wir uns den zweiten Term an.
Auch hier interessiert uns als erstes der Betrag:

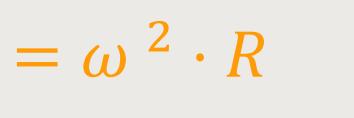
Das ist nichts anderes als die Normalbeschleunigung.
Daraus ergibt sich:
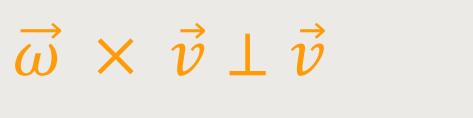
Und das bedeutet seinerseits, dass der zweite Term die „Normalbeschleunigung”
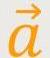 n ist.
Da diese zum Kreismittelpunkt gerichtet ist, nennt man sie auch
„Zentripetalbeschleunigung”.
n ist.
Da diese zum Kreismittelpunkt gerichtet ist, nennt man sie auch
„Zentripetalbeschleunigung”.
Bei einer Kreisbewegung mit konstanter Winkelgeschwindigkeit wird es keine Tangentialbeschleunigung geben. In diesem Fall gibt es nur eine Normalbeschleunigung. Und daher bleibt auch der Betrag des Geschwindigkeitsvektors konstant.
In diesem Zusammenhang gibt es noch die „Zentrifugalkraft”. Darunter versteht man eine Trägheitskraft, die in bewegten und beschleunigten Bezugssystemen eine Rolle spielt. Wenn man, wie oben beschrieben, ein rotierendes Bezugssystem betrachtet, dann wirkt auf das Teilchen eine „nach außen” gerichtete Trägheitskraft, nämlich diese Zentrifugalkraft. Und die Zentripetalbeschleunigung ruft ihrerseits eine entsprechende „nach innen” gerichtete „Zentripetalkraft” hervor, die notwendig ist, um die nach außen gerichtete Zentrifugalkraft zu kompensieren, sodass das Teilchen nicht hinausfliegt.
⇦ Kapitel Kapitel ⇨
