Wir werden im Nach­folgenden eine Bahnkurve kennen­lernen, bei der die Beschleunigung stets senkrecht auf die Bewegungs­richtung steht. Daraus ergibt sich dann auto­matisch, dass die Komponente der Tangential­beschleunigung gleich Null ist. Wobei sich der Betrag der Geschwindig­keit dementsprechend nicht ändert, sondern nur ihre Richtung.

Hier wird vorausgesetzt, dass die Beschleunigung Null ist:

Das ist die Bewegungs­gleichung für die unbeschleunigte Bewegung.

Letzten Endes ist dies eine Differential­gleichung, die integriert werden muss. Wenn man eine solche Integration durch­führt, erhält man eine „Integrations­konstante”:

Derartige Integrationen kann man sich verständ­lich machen, indem man umgekehrt zurück differen­ziert. Um das zu lösen, wird immer eine Anfangs­bedingung benötigt:

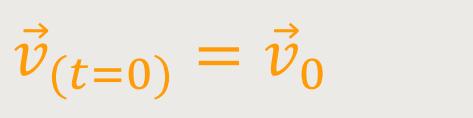
Damit ergibt sich:

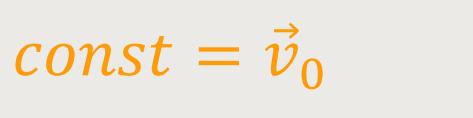
Und das bedeutet:

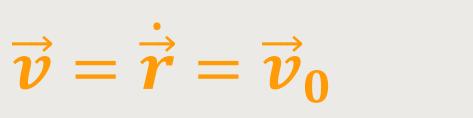
Wenn man wieder eine Integration durchführt, erhält man eine weitere Integrations­konstante:

Es wird wieder eine Anfangsbedingung benötigt:

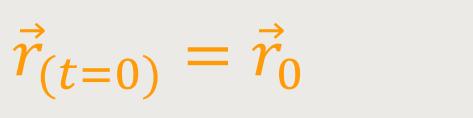
Damit ergibt sich analog zu oben:

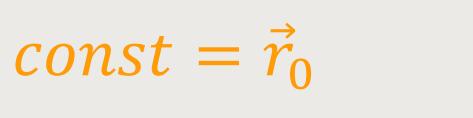
Und das bedeutet:

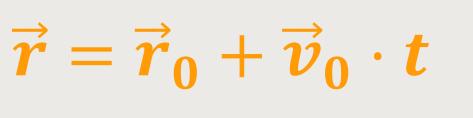
Und damit erhält die Bahn­kurve konkret fest­gelegt. So ergibt sich für positive und negative Zeiten eine gerad­linige gleich­förmige Bewegung.

Jetzt wird vorausgesetzt, dass die Beschleunigung „gleichförmig” ist:

Das ist die Bewegungs­gleichung für die gleich­förmig beschleunigte Bewegung.

Wenn man analog zu oben eine Integration durch­führt, erhält man auch hier eine Integrations­konstante:

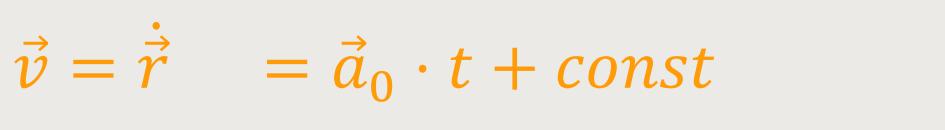
Es wird wieder eine Anfangs­bedingung benötigt:

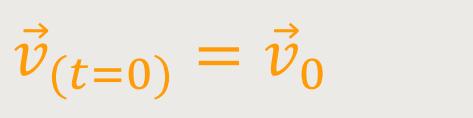
Damit ergibt sich:

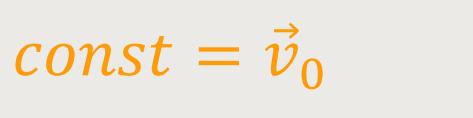
Und das bedeutet:

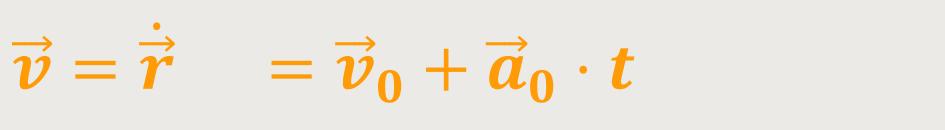
Wenn man abermals eine Integration durch­führt, erhält man auch hier eine weitere Integrations­konstante:

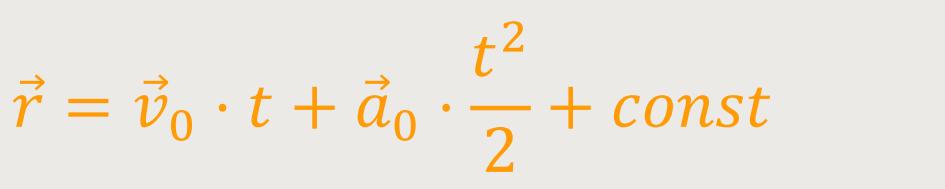
Auch hier wird eine Anfangsbedingung benötigt:

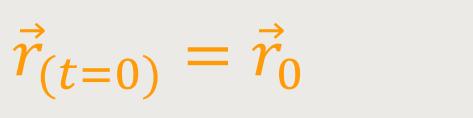
Damit ergibt sich analog zu oben:

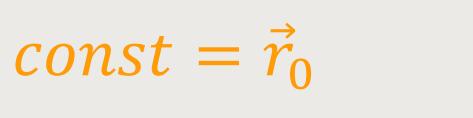
Und das bedeutet:

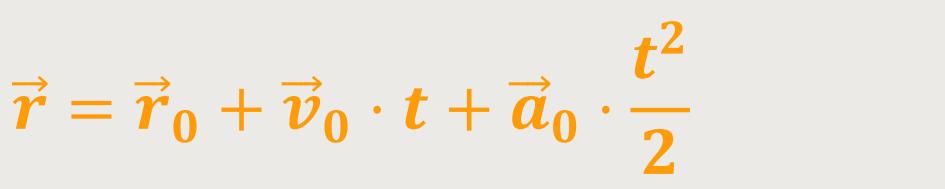
Und damit erhält man den Ausdruck für den „Orts­vektor als Zeit­funktion”.
Und damit lässt sich auch der Orts­vektor für eine andere Situation definieren, nämlich für den freien Fall.

Zunächst legt man in gewohnter Weise ein paar Rahmen­bedingungen fest:

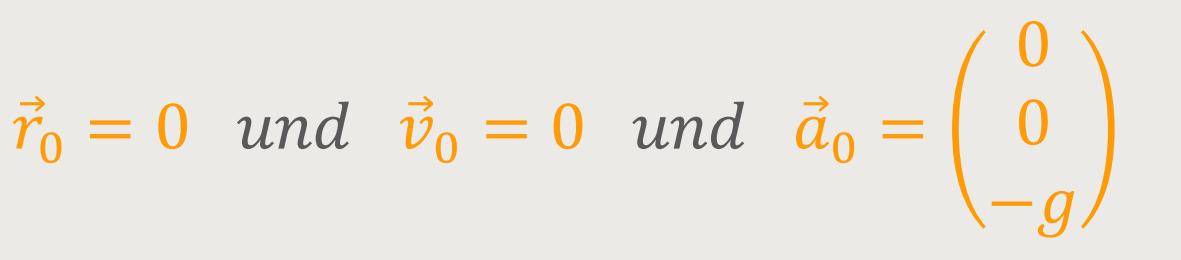
Die Fall­beschleuni­gung ist einfach eine nach unten gerichtete Beschleunigung. Wenn bei der Betrachtung ein „oben” und „unten” eine Rolle spielt, schaut die z-Achse bzw. die x₃-Achse nach oben.

Wenn die Rahmen­bedingungen fest­liegen, kann man zunächst die Geschwindig­keit für den gleich­förmig beschleunigten freien Fall ausrechnen:

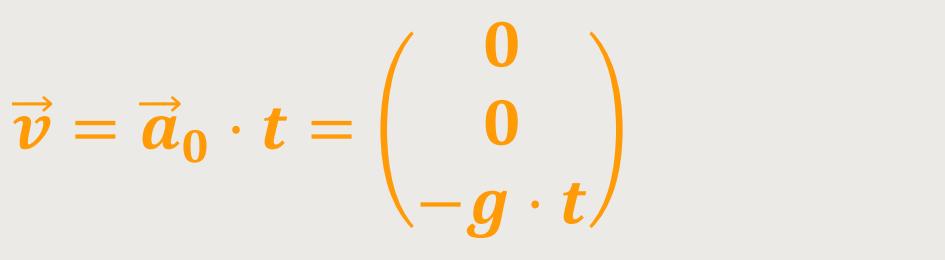
Und für den Orts­vektor ergibt sich:

Mit diesen beiden Ausdrücken erhält das Fall­gesetz. Aller­dings nur unter der Voraus­setzung, dass beim freien Fall tatsächlich eine gleich­förmig beschleunigte Bewegung vorliegt. Und das wäre zum Beispiel im Gravitations­feld nahe der Erdober­fläche gegeben.

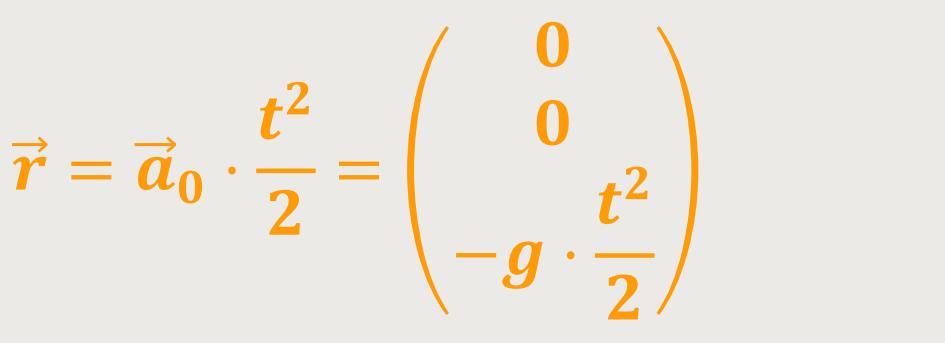
Was passiert aber, wenn die Situation etwas komplizierter wird? Nehmen wir hierzu den „schrägen Wurf”.

Zunächst legt man wieder ein paar Rahmen­bedingungen fest:

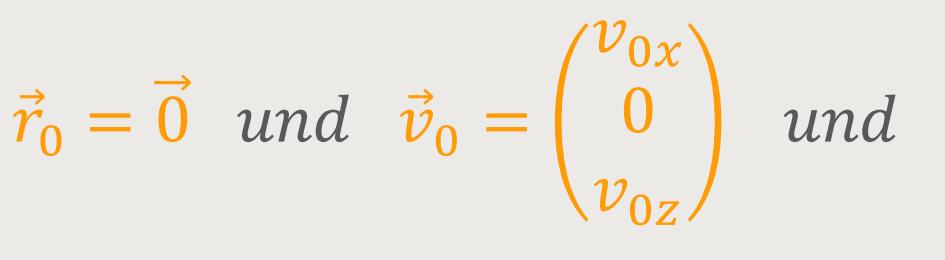
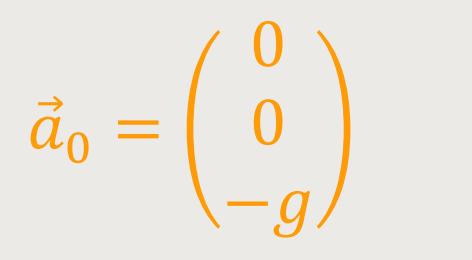
Die Wurf­beschleunigung ist einfach eine nach „schräg oben” gerichtete Beschleunigung. Wenn die Rahmen­bedingungen fest­liegen, kann man zunächst die Geschwindig­keit für den gleich­förmig beschleunigten freien Fall ausrechnen:

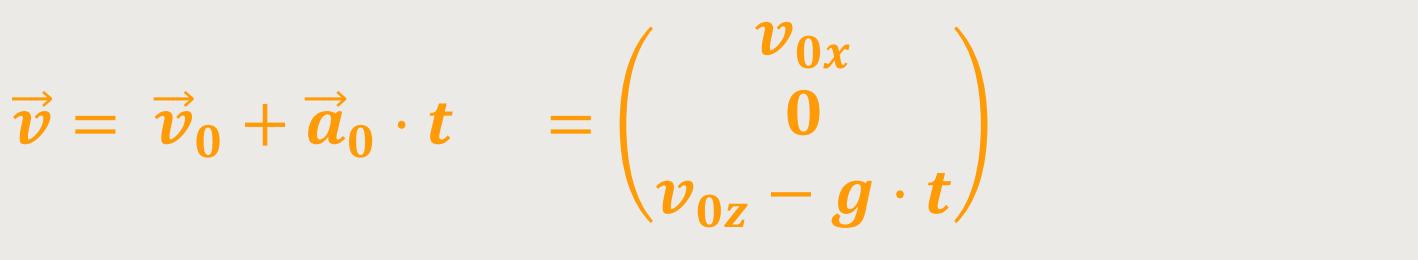
Und für den Orts­vektor ergibt sich:

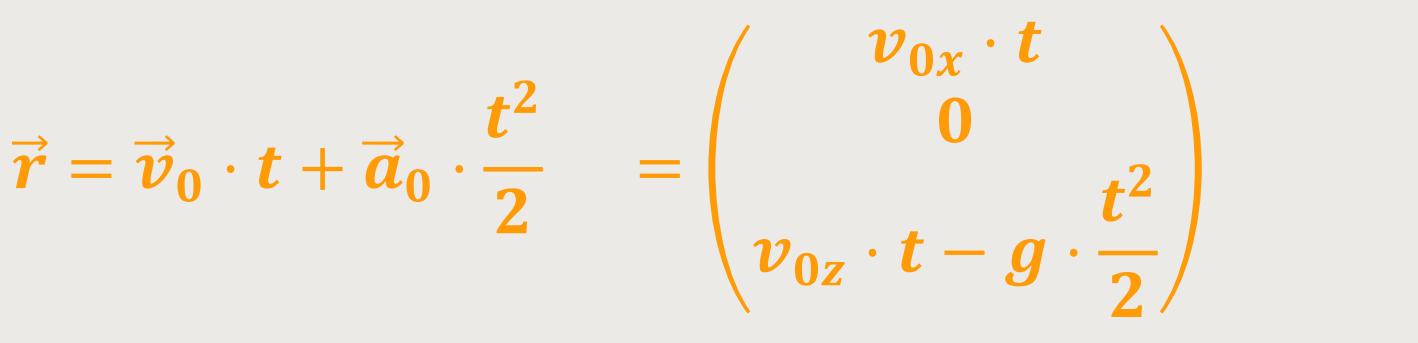
Mit diesen beiden Ausdrücken lässt sich die Bahn­kurve des „schrägen” Wurfes darstellen. Wenn man jetzt noch aus der Gleichung für den Orts­vektor t eliminiert, also t = x / v_0x, dann erhält man eine quadratische Gleichung in der x-z-Ebene:

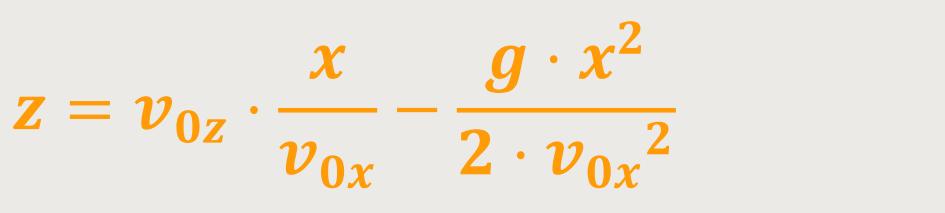
Das ist der Ausdruck für die Wurfparabel.

Zunächst einmal geht es um den Wurfwinkel:

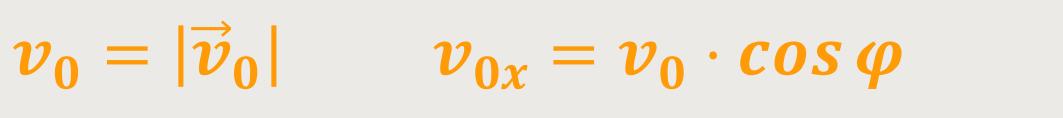
Jetzt verwendet man die Gleichung für die Wurfparabel und setzt die beiden x-z-Komponenten in Bezug zu dem Abwurfwinkel:

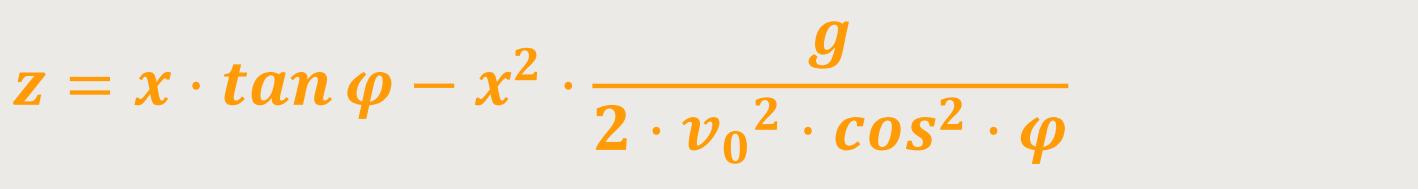
Die maximale Höhe der Wurf­parabel bezeichnet man vorzugs­weise mit H. Und die Weite dement­sprechend mit W. Um das H zu erhalten, führt man eine Kurven­diskussion durch.

Wenn man d_z / d_x = 0 setzt, erhält man die Wurf­höhe und die Wurfweite:

Bei dem Ganzen bleibt natürlich die „Luftreibung” unberück­sichtigt.

Wir verstehen unter Geschwindig­keit immer den gesamten Geschwindig­keits­vektor, bestehend aus den beiden Kompo­nenten. Und auch wenn sich der Betrag des Geschwindigkeits­vektors nicht ändert, ändert sich trotzdem die Geschwindig­keit, wenn sich die Richtung der Geschwindig­keit ändert.

⇦ Kapitel Kapitel ⇨