Wir werden uns jetzt in der Mechanik schritt­weise der Beschreibung von Bewegungen von Systemen zuwenden. Zunächst werden wir diese Betrachtung ohne die Frage nach der Ursache dieser Bewegungen vornehmen. Anschließend gehen wir der Sache näher auf den Grund, denn wir möchten ja auch wissen, wodurch es bewirkt wird, dass sich gewisse Körper so bewegen, wie sie sich bewegen.

Zunächst befassen wir uns mit der Bewegung von Massen­punkten oder Teilchen. Das sind Systeme, wo es zunächst auf die innere Struktur nicht ankommt. Meistens handelt es sich hierbei um kleine Systeme. Man kann nämlich mithilfe dieser Massenpunkt­mechanik sehr viele wichtige Dinge beschreiben und anschließend gedanklich auf größere Systeme über­tragen.

Bei der „Kinematik” geht es darum, die Bewegung von Massen­punkten (Teilchen) zu beschreiben. Dazu werden „Bezugs­systeme” zugrunde gelegt. So ein Bezugs­system hat 3 Raum­koordinaten und 1 Zeit­koordinate. Wir befinden uns zwar in einem 3-dimensionalen Raum, aber es bietet sich grund­sätzlich an, diese Vorgänge in einem 4-dimensionalen System zu betrachten.

Im Rahmen der klassischen Physik, also wenn man keine zu großen Energien und Geschwindig­keiten zulässt, kann man der „Zeit” eine Sonder­rolle zuweisen. Und zwar sieht man diese als absolut an, sprich die Zeit „verfließt” einfach. Für unsere Betrach­tungen in der klassischen Mechanik ist das eine sehr gute Näherung.

Bei Annäherung an die Licht­geschwindig­keit jedoch stellt sich heraus, dass die Physik nicht nur ein bisschen anders wird, sondern gravierend anders. Das war seinerzeit schon dem Newton suspekt, und so schrieb er in seinen schrift­lichen Aufzeich­nungen über die Zeit: „Die absolute, wahre, und mathe­matische Zeit verfließt an sich und vermöge ihrer Natur gleich­förmig und ohne Beziehung auf irgend einen äußeren Gegen­stand“ (Prinzipia).
Obwohl dies in der Realität nicht der Fall ist, beschränken wir uns zunächst darauf, dass die Zeit eine „absolute Größe” sei. Die Raum­koordinaten unseres Bezugs­systems werden wir meistens als „kartesische Koordinaten” einführen (x, y, z) bzw. (x₁, x₂, x₃).

Wir leben in einer 3-dimensionalen räum­lichen Welt. Das können wir durch unsere Wahr­nehmung und durch die Experimente gut beobachten. Und das entspricht einfach unserer Vorstellungs­kraft. Mit der 4. Dimension werden wir uns später noch befassen. Das erste, was man bei so einem Massen­punkt wissen möchte ist, wie bewegt er sich im Raum. Was für eine „Bahn­kurve” verfolgt er? Man möchte also die zeit­abhängige Position im Raum bestimmen. Das geschieht im Wesent­lichen in Form einer „Parameter­darstellung”.

Man geht davon aus, es gibt einen Ursprung. Im All­gemeinen ist das auch der Nullpunkt eines Bezugs­systems. Und dann gibt es noch einen Punkt P, an dem sich dieses Teilchen gerade befindet. Diesen beschreiben wir mit Hilfe des Orts­vektors (vom Ursprung zum jeweiligen Punkt hin). Dieser Orts­vektor hat dann die Koordinaten x-y-z. Das sind die Komponenten des Orts­vektors und damit gleich­zeitig die Koordinaten des Punktes, wo dieses Teilchen gerade ist. Und wenn sich dieses Teilchen entlang einer Bahn­kurve bewegt, wird dieser Orts­vektor zu verschiedenen Zeiten verschiedene Werte annehmen (t₁), (t₂).
Und so bewegt sich dann dieser Massen­punkt längs einer solchen Bahnkurve.

Dieser zeitabhängige Ortsvektor ist dann:

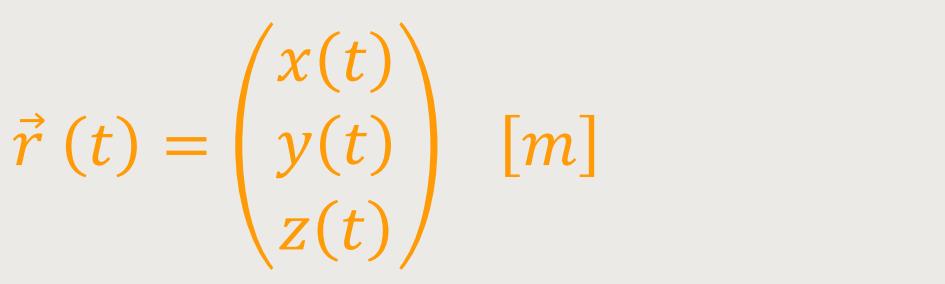
Das trifft aber nur im Rahmen der klassischen Mechanik zu. Im Rahmen der Quanten­mechanik zeigt sich, dass man aufgrund der Unschärfe­relation niemals gleich­zeitig Ort und Impuls genau wissen kann. Und weil man damit die Geschwindig­keit nicht messen kann, verschwimmt die Bahn­kurve. Genau­genommen gibt es gar keine Bahn­kurve im Bereich der Quanten­mechanik, vor allem wenn die Teilchen zu klein werden.

In vielen Bereichen reicht die klassische Mechanik aber aus, und die Unsicher­heiten oder Fehler aufgrund relativis­tischer oder quanten­mechanischer Effekte sind vernach­lässigbar. Und damit ist die klassische Mechanik die gegebene Theorie für das jeweilige Anwendungs­problem. Und nur wenn man an ihre Gültigkeitsgrenzen geht, muss man wachsam sein.

Bei dem Begriff „Theorie” handelt es sich um eine formale Beschreibung von physika­lischen Systemen im Rahmen bestimmter Gültigkeits­grenzen. Es ist solange etwas Gutfundiertes, solange es noch nicht widerlegt werden konnte, wohlbemerkt immer im Rahmen der „Gültigkeits­grenzen”. Und Gültigkeits­grenzen werden oft erst im Lauf der Zeit sichtbar, wenn die Beobachtungs­möglich­keiten es erlauben. Aber die Bewegung der Teilchen lässt sich noch weiter beschreiben.

Die „Geschwindig­keit” ist der Weg pro Zeit­einheit. In diesem Fall betrachten wir die vektoriell beschriebene Positions­änderung pro Zeit­einheit. Der Geschwindig­keits­vektor wird definiert als die „Positions­änderung” pro Zeiteinheit:

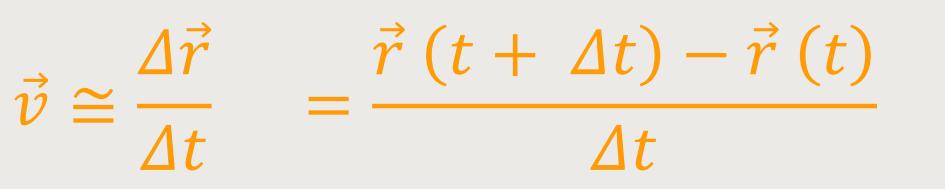
Wenn wir zum Beispiel einen Orts­vektor auf einer Bahn­kurve betrachten, jeweils ausgehend vom Nullpunkt unseres Bezugs­systems, dann wird daraus zunächst einmal der Orts­vektor (t) zu einem bestimmten Zeit­punkt. Nach Verstreichen einer kurzen Zeit wird daraus der zeit­abhängige Orts­vektor (t + Δt). Betrachtet man jetzt dieses kurze Zeit­intervall Δt etwas näher, dann ergibt sich nämlich eine Positions­verschiebung, und das nennt man Δ. Als Ergebnis erhält man einen Tangenten­vektor an die Bahn­kurve. Die Länge dieses Vektors gibt die „speed” oder den Betrag an. Das Δt ist natürlich noch nicht klein genug. Klein genug wird es erst, wenn man den Grenzwert betrachtet:

Das ist die Definition der Geschwindig­keit. Die Einheit ist [m/s]. Der Betrag || ist der zurück­gelegte Weg pro Zeiteinheit.

Ähnlich verhält es sich mit der Beschleuni­gung. Der Beschleunigungs­vektor wird auch definiert als die „Positions­änderung” pro Zeiteinheit.

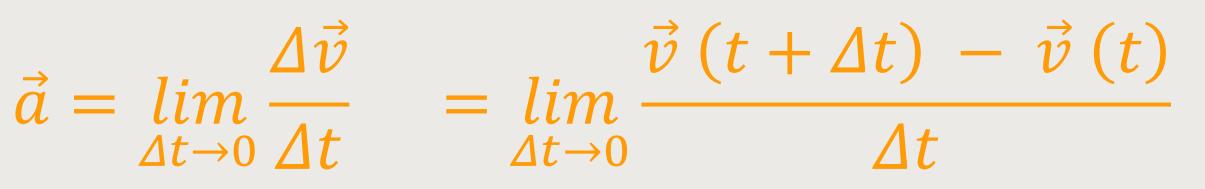
Durch den „Limes” ist das konkret ein Differenzial­quotient.

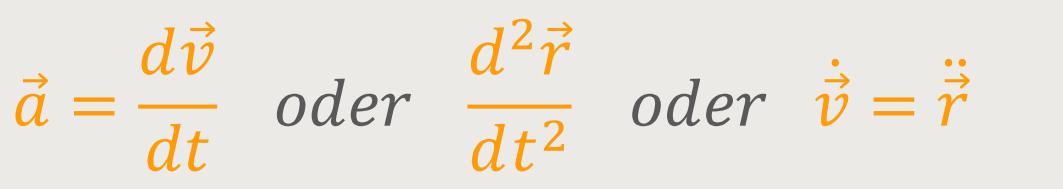
Der Beschleunigungs­vektor 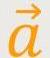wird nun nicht notwendiger­weise tangential an der Bahn­kurve liegen. Und deshalb unter­scheidet man den tangentialen Teil der Beschleunigung. Das ist die Komponente des Beschleunigungs­vektors, die tangential zur Bewegungs­richtung liegt. Diese Komponente nennt man auch die „Tangential­beschleunigung” 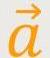_t.

Zusätzlich gibt es noch die andere Komponente, nämlich die „Normal­beschleunigung” _n. Beide zusammen ergeben den „Beschleunigungs­vektor”.

Das ist die Definition der Beschleunigung. Die Einheit ist [m/s²]. Das ist die Geschwindigkeits­änderung pro Zeit­einheit. Also um wie viel Meter pro Sekunde sich die Geschwindig­keit pro Sekunde ändert.

Zusammen­fassend lässt sich sagen: Der Geschwindigkeits­vektor wird immer tangential an der Bahnkurve liegen. Der Beschleunigungs­vektor kann tangential an der Bahn­kurve anliegen, muss es aber nicht.

⇦ Kapitel Kapitel ⇨