Und es geht doch − mit einer Genauigkeit von 99,96 % bzw. einer Abweichung von lediglich 0,04 %.
Die Quadratur des Kreises ist ein klassisches Problem der Geometrie. Die Aufgabe besteht darin, aus einem vorgegebenen Kreis in endlich vielen Schritten ein Quadrat mit dem gleichen Flächeninhalt zu finden, sprich die Konstruktion eines Quadrats mit der Seitenlänge √ π. Sie ist äquivalent zur sogenannten Rektifikation des Kreises, also der Konstruktion einer geraden Strecke, die dem Kreisumfang entspricht. Das wiederum entspricht der Konstruktion der Kreiszahl π (halber Kreisumfang) aus der Strecke, deren Länge gleich 1 Längenmaßeinheit ist.
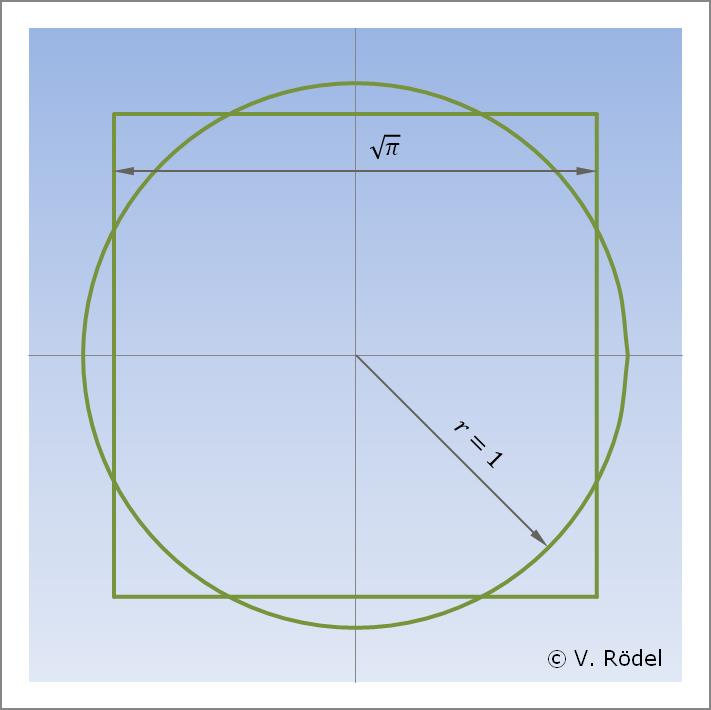
Abb. 1: Das Quadrat und der Kreis haben den gleichen Flächeninhalt.
Die Quadratur des Kreises gehört zu den populärsten Problemen der Mathematik. Die Redewendung „Quadratur des Kreises” ist im allgemeinen Sprachgebrauch zu einer Metapher für eine unlösbare Aufgabe geworden.
In der Mathematik heißt eine reelle oder komplexe Zahl transzendent, wenn sie nicht Nullstelle eines (vom Nullpolynom verschiedenen) Polynoms mit ganzzahligen Koeffizienten ist. Andernfalls handelt es sich um eine algebraische Zahl. Jede reelle transzendente Zahl ist überdies irrational. Erst im Jahre 1882 konnte dies von dem deutschen Mathematiker Ferdinand von Lindemann bewiesen werden.
Beschränkt man die Konstruktionsmittel auf Zirkel und Lineal, so ist die Aufgabe aufgrund der Transzendenz von π unlösbar.
Dennoch erhebt sich die Frage: Gibt es zumindest ein Näherungsverfahren? Vielleicht gelingt es uns ja, mit einer geringstmöglichen Abweichung nahezu gleichgroße Flächen nur mithilfe eines Zirkels und eines Lineals zu konstruieren. Wobei das Lineal keine Maßeinteilung haben darf.
Mit dem nachfolgenden Konstruktionsverfahren lässt sich eine Abweichung von lediglich 0,04 % erzielen!
Wir zeichnen z. B. auf einem DIN A4 Blatt zunächst mit dem Zirkel einen anschaulich großen Kreis. Obwohl wir den Radius bewusst nicht abmessen, soll er aber zum besseren Nachvollziehen genau 100 mm betragen. Dann zeichnen wir eine waagerechte Gerade durch den Mittelpunkt des Kreises, wobei diese Linie den Kreis beidseitig berührt. Nun konstruieren wir die Lotrechte auf die vorhandene Linie. Dazu schlagen wir mit dem Zirkel zwei Halbkreise mit einem Radius r · 2, der dem Durchmesser des vorgegebenen Kreises entspricht. Wenn wir die beiden Schnittpunkte verbinden, erhalten wir im rechten Winkel eine Lotrechte zur Grundlinie.
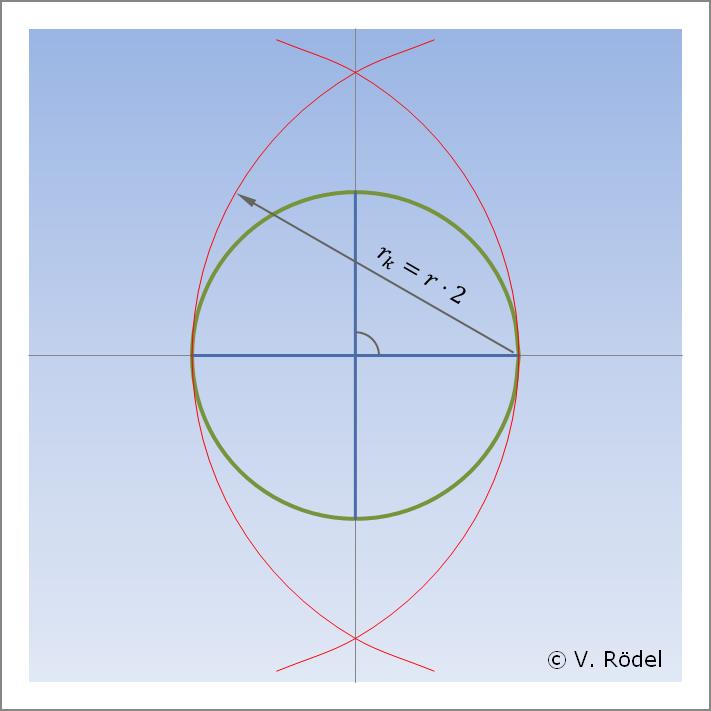
Abb. 2: Konstruieren einer Lotrechten auf einer Grundlinie.
Damit ergibt sich eine Kreisfläche mit einem Flächeninhalt π · r². Bei einem Radius von 100 mm wären das z. B. A = 31415,9265 mm². Zieht man aus diesem Wert die Wurzel, erhalten wir die Seitenlänge des gesuchten Quadrats. Das Quadrat müsste dann in unserem Fall eine Seitenlänge von a = 177,2454 mm haben.
Ziel ist es also, nur mithilfe von Zirkel und Lineal sowie mit möglichst wenig Schritten ein Quadrat zu konstruieren, dass den gleichen Flächeninhalt wie der vorgegebene Kreis hat.
Nun schlagen wir 4 weitere Halbkreise mit dem Radius r, wobei die Mittelpunkte den Schnittpunkten (Endpunkten) der beiden lotrechten Linien am Kreisumfang entsprechen. Anschließend zeichnen wir 2 diagonale Hilfslinien H1 und H2 ein, dessen Enden mit den Schnittpunkten der Halbkreise zusammentreffen. Es entsteht eine Art „Blattmuster”.
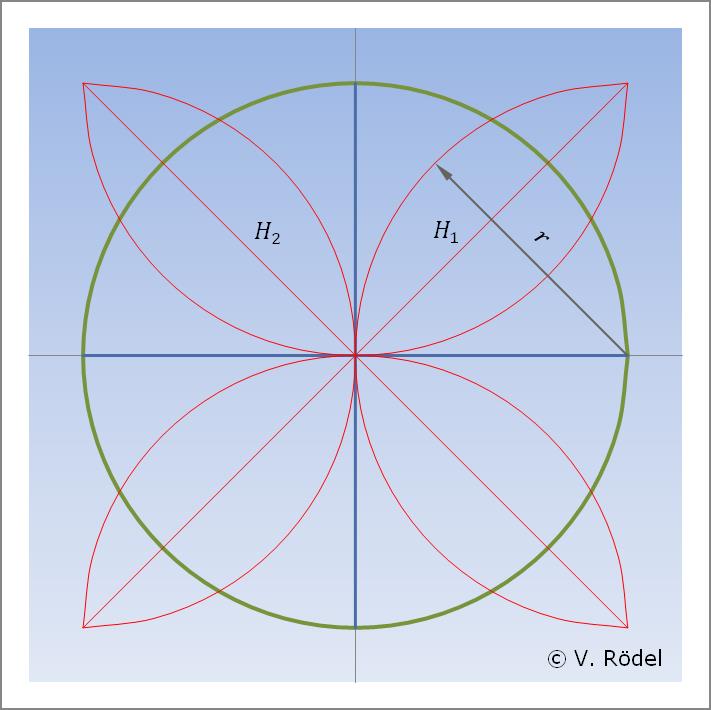
Abb. 3: Konstruieren der diagonalen Hilfslinien (45°).
Nun könnten wir durch die so entstandenen 8 Schnittpunkte
auf dem Kreisumfang 4 Linien einzeichnen, die exakt ein
Quadrat ergeben (orange). Die Seitenlänge beträgt
a = 173,2051 mm und würde einen
Flächeninhalt von exakt A = 30000,00 mm²
ergeben. Das wären immerhin schon 95,49 % vom angestrebten
Hinweis: Die obere „grüne” Linie dient als Referenzlinie.
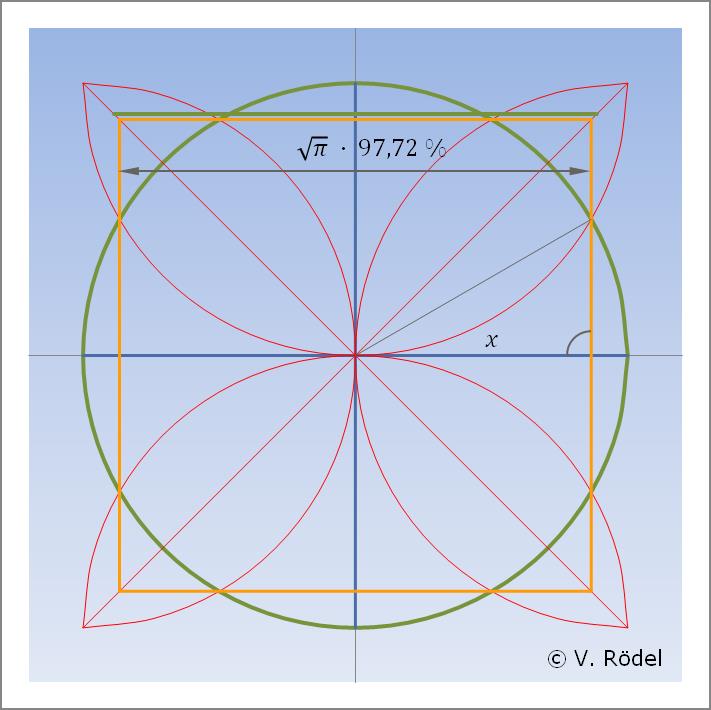
Abb. 4: Erster Versuch − Abweichung 4,5 %.
Geht es noch genauer? Ja, das ist der Fall.
Zur besseren Betrachtung vergrößern wir zunächst den oberen rechten Bereich und zeichnen eine Hilfslinie H2 ein, die geometrisch bedingt genau unter 30° angeordnet ist. Auf dieser Hilfslinie tragen wir mit einem Zirkel 10 kleine, gleichgroße Teilabschnitte auf. Anschließend werden mithilfe der Parallellinien-Konstruktion diese Abschnitte auf die diagonale Hilfslinie H1 übertragen. Genau 7/10 vom Kreisradius r1, schlagen wir einen kleinen Kreis mit dem Radius r3 = 3/10. Dadurch ergeben sich die Schnittpunkte S1 und S2 auf dem großen Kreisumfang.
Hinweis: Wir wissen zwar, dass im vorliegenden Fall der Radius des kleinen Kreises 30 mm beträgt, aber bei einem willkürlich vorgegebenen Ausgangskreis wissen wir nicht, wie viel 3/10 entspricht.
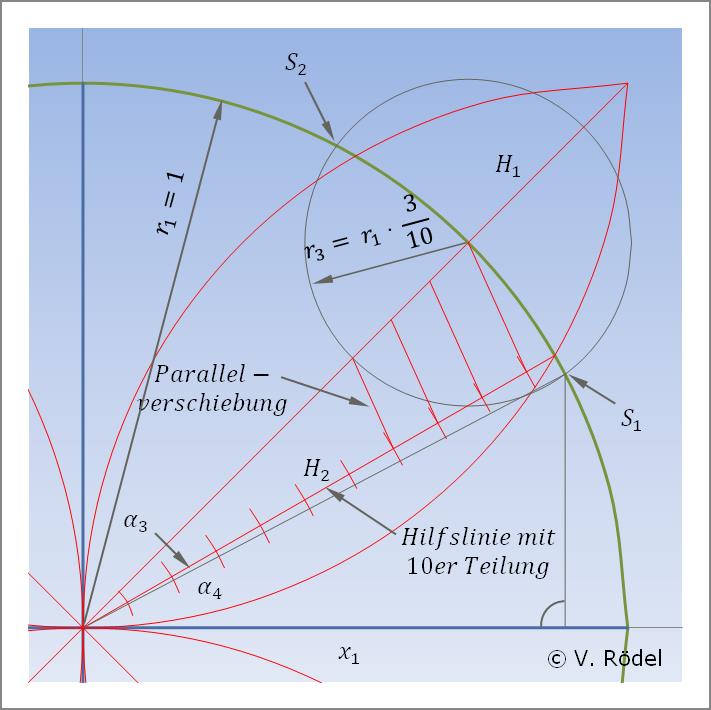
Abb. 5: Konstruieren der
Zur Kontrolle ermitteln wir auf Grundlage des Kosinussatzes die beiden
Teilwinkel vom Gesamtwinkel 30°, und entsprechend den
x-Wert des Schnittpunktes S1.
Mit a/2 = 88,5019 mm und einer entsprechenden
Seitenlänge von a = 177,0038 mm und damit einen
Flächeninhalt von A = 31330,3381 mm². Das sind
bereits 99,73 % vom angestrebten
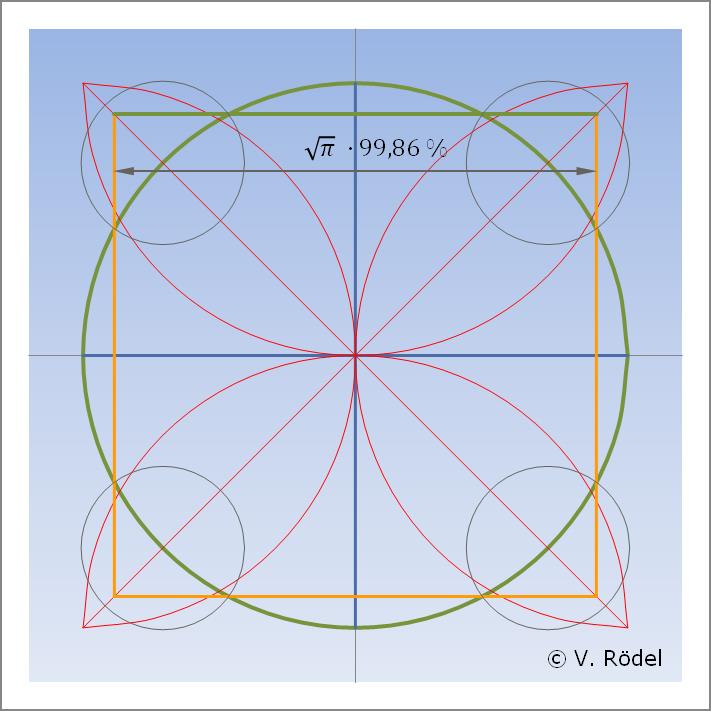
Abb. 6: Zweiter Versuch − Abweichung 0,27 %.
Mithilfe des Kosinussatzes können wir uns an den Grenzwert herantasten, und erhalten schließlich einen Wert für den kleinen Radius r3 von 30,2572 mm. Das wäre der „exakte” Radius des kleinen Kreises bei einem Ausgangskreis mit einem vorgegebenen Radius r1 von 100 mm.
Zur Erinnerung: In der Realtiät dürfen wir nur mit einem Lineal „ohne” Maßeinteilung konstruieren.
Und wir fragen uns ein letztes Mal: Geht es noch genauer? Ja, das ist der Fall.
Der dritte Schritt wurde nur eingefügt, um den Spannungsbogen hochzuhalten. Im Grunde können wir auch gleich gemäß dem vierten Schritt vorgehen.
Hierzu verbinden wir zunächst die Eckpunkte der beiden lotrechten Linien und
erhalten eine weitere diagonale Hilfslinie H3, die
zugleich die bereits vorhandene Diagonale H1 halbiert.
Anschließend zeichnen wir einen innenliegenden Tangentialkreis
r2 mit dem Radius
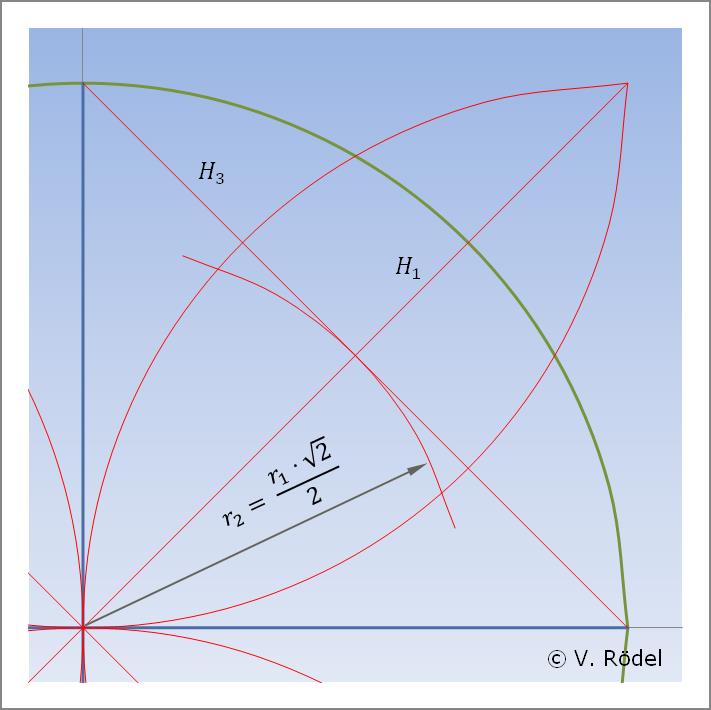
Abb. 7: Konstruieren einer Seitenhalbierenden mit Tangentialkreis.
Sowohl die neue Hilfslinie H3 als auch der Tangentialkreis r2 schneiden die „Blattkontur” an jeweils 2 Punkten. Einer dieser Schnittpunkte dient jetzt als Mittelpunkt für einen weiteren kleinen Kreis K1. Der Radius dieses Kreises soll mit dem Punkt zusammentreffen, wo sich der Schnittpunkt des Tangentialkreises r2 mit der Blattkontur befindet. Den so ermittelten Radius übertragen wir auf den eigentlichen Tangentialpunkt, indem wir dort einen zweiten Kreis K2 übertragen.
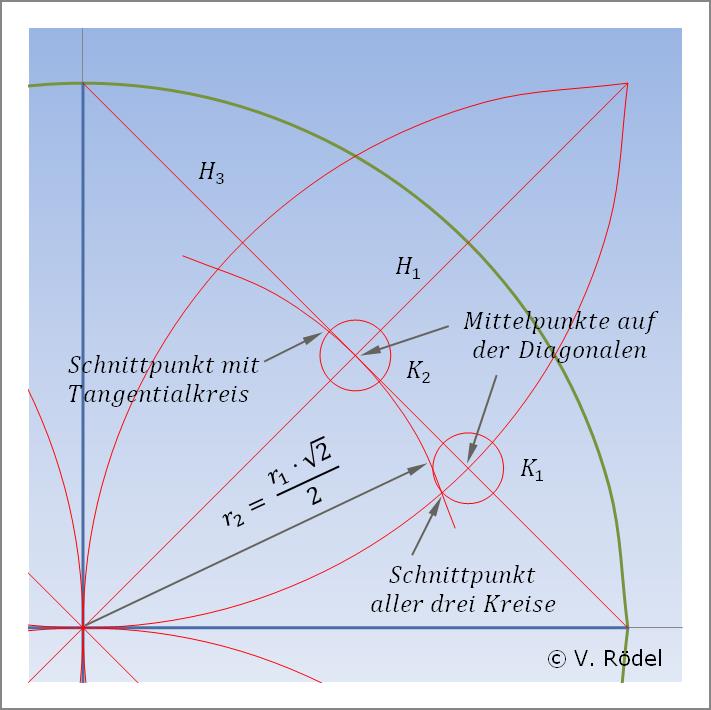
Abb. 8: Konstruieren eines Hilfskreises K1 mit Übertrag nach K2.
Bei genauem Hinschauen kann man erkennen, dass dieser zweite „kleinste” Kreis K2 mit dem Tangentialkreis r2 nochmals zwei Schnittpunkte bildet. Diese Punkte ergeben dann den Radius des bereits unter Schritt drei beschriebenen mittelgroßen Kreises r3 mit dem Wert 3/10 + x. Im vorliegenden Fall sind das 30 mm + x.
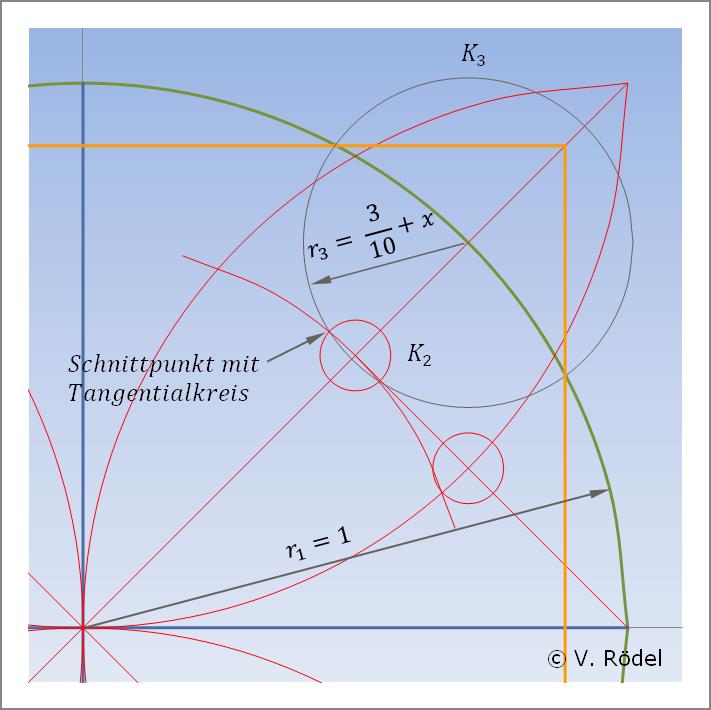
Abb. 9: Konstruieren des finalen Hilfskreises K3.
Wie unschwer zu erkennen ist, kann es sich nur um ein paar Zehntel handeln. Eines vorweg: Die orangen Seitenlinien des Quadrats liegen nahezu genau über dem anfänglich gesuchten grünen Zielquadrat. Aber auf was für Werte kommen wir genau? Um das herauszufinden, folgt jetzt eine rechnerische Beweisführung.
In dem nachfolgenden Eingabefeld kann ein individueller Radius eines Ausgangskreises eingetragen werden. Der Vorgabewert ist in diesem Fall 100 mm. Alle anderen Werte, die man nur mithilfe von Zirkel und Lineal nach obiger Beschreibung konstruiert, ergeben sich zwangsläufig.

Abb. 13: Konstruktionsverfahren mit lediglich 23 Schritten.
Streng mathematisch betrachtet ist die „Quadratur des Kreises” eine unlösbare Aufgabe. Denn mit den beiden irrationalen Zahlen π und √2 lassen sich keine zwei exakt gleichgroße Flächen darstellen.
Aus Sicht des Näherungsverfahrens allerdings ist es möglich, bis auf 4/100 genau einen nahezu gleichen Flächeninhalt nur mithilfe eines Zirkels und eines Lineals in lediglich 23 Schritten zu konstruieren, wobei der obige dritte Schritt übersprungen wird.
Des Weiteren stellt sich heraus, selbst wenn der gewählte Radius des Ausgangskreises größer wird, bleibt die Abweichung mit 0,04 % konstant.
⇦ Kapitel Kapitel ⇨
