In den vor­herigen Kapiteln haben wir die Einzig­artig­keit des Golden Schnitts und des Goldenen Winkels in Ver­bindung mit der Fibonacci-Folge kurz beleuchtet. Ohne Zweifel stehen alle drei Phänomene eng mitein­ander in Verbin­dung. Sie lassen sich alle­samt in der sogenannten Goldenen Spirale wieder­finden. Wie bereits erwähnt, liegen diesen einzig­artigen Mechanismen Zahlen­verhält­nisse zugrunde, die durch irratio­nale Zahlen beschrieben werden. Aller­dings entsteht bei genauerer Betrachtung ein nicht zu vernach­lässigendes Problem.

Wie sich in der Natur deutlich zeigt, spielen nicht die ganzen Zahlen, sondern vor allem die irratio­nalen Zahlen eine wesent­liche Rolle. Denken wir nur an zwei der wichtig­sten Naturkonstanten: π (pi) und √2.
Die Fibonacci-Folge basiert zwar grund­sätzlich auf Brüchen und deren Zahlen­verhältnissen. Des Weiteren wird der Quotient auf­einander­folgender Zahlen der Fibonacci-Folge als Natur­konstante Φ (Phi) bezeichnet und stellt als Ergebnis eben­falls eine irratio­nale Zahl dar.

Doch die Zahlenreihe, sowie deren grafische Dar­stellung, beginnen im Regel­fall mit der Zahl Eins. Aber selbst, wenn man in der Zahlen­reihe optional die Zahl Null mit berück­sichtigt, entspricht das nicht der Realität. Der Linien­zug bzw. der Kurven­verlauf wird hierbei aus Viertel­kreisen gebildet. Der Radius dieser Viertel­kreise ist allen­falls das Verhältnis ganzer Fibonacci-Zahlen.

Die Fibonacci-Folge als Spirale visualisiert, spiegelt lediglich die Zahlen­verhältnisse wider, und damit die statis­tische Anzahl der in der Natur vorkommenden Blüten­blätter. Der Kurven­verlauf ent­spricht aber nicht einmal annähernd der tatsäch­lichen Anordnung bzw. Verteilung der Samen, wie zum Beispiel beim Blüten­korb einer Sonnenblume.

Aus diesem Grund wird die Goldene Spirale, wie im vorherigen Kapitel betrachtet, zweck­mäßig mit der Natur­konstante Φ (Phi) beschrieben. Nach­folgend noch­mals die Gegen­über­stellung beider Spiralen, um den unmittel­baren Unter­schied aufzuzeigen.

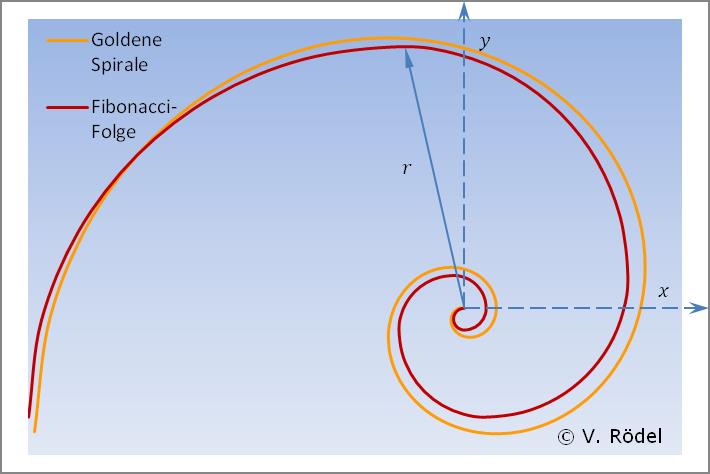
Abb.: Gegenüber­stellung der Goldenen Spirale mit der Fibonacci-Folge

In der Realität muss eine Grenz­wert­bildung gegen unend­lich in Betracht gezogen werden, zumindest aber bis in den Bereich der moleku­laren Strukturen. Eine Formel, die dieser Voraussetzung genügt, müsste demnach einen leicht veränderten „Quellcode” haben.

Alle Pflanzen und Lebe­wesen weisen in ihrem Bau­plan spiralige Struk­turen auf. Manches ist offen­kundig erkenn­bar, wie beispiels­weise bei einem Schnecken­haus. Oder fossile Beispiele sind die Ammoniten. Die „Anordnung” dieser biologisch erzeugten Spiralen, die meistens auf Logarith­mischen Spiralen beruhen, lehnt sich vom Grund­satz her an der Fibonacci-Folge an.

Andere nicht so offen­kundige Spiral­strukturen, wie zum Beispiel die Doppel­helix unserer DNA, bleiben dem sicht­baren Auge zunächst verborgen. Erst die genaue Betrachtung des mensch­lichen Bauplans zeigt eben­falls manig­faltige Spiralmuster auf.

In der Physik vollführt ein elektrisch geladenes Teilchen, das sich in einem Magnet­feld bewegt, eine „Spiralbahn”. Voraus­setzung ist, dass sich das Teilchen nicht parallel, anti­parallel oder quer zur Nord-Süd-Ausrichtung des Magnet­feldes bewegt. Die Kraft, die das Teilchen auf eine spiral­förmige Bahn zwingt, heißt Lorentz­kraft. Streng genommen ist diese Flug­bahn aber eine Art Schrauben­linie. Bei der Bewegung parallel oder anti­parallel zur Nord-Süd-Ausrichtung des Magnet­feldes entsteht eine gerade Flug­bahn, und bei der Bewegung quer zur Nord-Süd-Ausrichtung des Magnet­feldes entsteht eine Kreis­bahn.

Wenn ein elektrisch geladenes Teilchen auf einer sol­chen Kreis­bahn Energie durch elektro­magnetische Strahlung abgibt, dann bewegt es sich auf einer immer enger werdenden Spiral­bahn. Die schrauben­förmige Flug­bahn des elektrisch geladenen Teilchens ist eine Über­lagerung einer geraden Flug­bahn und einer Kreis­bahn. Bei Energie­verlusten durch elektro­magnetische Strahlung und auch in inhomogenen Magnet­feldern, entstehen konische Spiralen aus der Über­lagerung von Schraube und Spirale.

Bei den ganzen Über­legungen darf man aller­dings nicht vergessen, dass wir grund­sätzlich zwischen statischen und dynamischen Prozessen unter­scheiden müssen. Ein Schnecken­haus zum Beispiel ist im eigentlichen Sinne ein statisches Objekt, welches offen­kundig während seines immens lang­samen Wachstums sehr gut durch eine „Logarithmische Spirale” abgebildet werden kann. Darüber hinaus handelt es sich größten­teils bei den bisher betrachteten Spiralen um „ebene” (flache) Spiralen, deren Geometrie sich vornehmlich für 2-dimesionale Darstellungen eignet.

Blumen dagegen scheinen zwar bei ihren Blüten­körben auf ihren ersten Blick auch eine 2-dimesionale Spiral­anordnung zu zeigen, aber in Wirklich­keit vollzieht sich das Wachstum mehr­dimensional. Die Pflanze muss als gesamte Einheit betrachtet werden. Neben ihrer 3-dimensionalen Grund­struktur zeigt sich im Detail bei Zeit­raffer­aufnahmen, dass die Wachstums­bewegung noch hinzukommt, die noch­mals eine eigene Spiral­bewegung vollzieht.

Wenn wir diesen Aspekt eben­falls berück­sichtigen wollen, sind wir sogar auf der Suche nach einer Spirale, die sich bevorzugt für den 4-dimensionalen gekrümmten Raum eignet.

Dies kann man am Blüten­korb der Sonnen­blume bzw. der späteren Anordnung der Samen sehr schön erkennen. Die Goldene Spirale bildet in den meisten Fällen nur die Grund­lage für die Anzahl rechts­läufigen und der links­läufigen Spiralkurven.

Abb.: Spiralmuster bei der Sonnenblume (rechtsdrehend)

Um exakte Spiral­kurven abbilden zu können, muss der Kurven­verlauf dem Wachstum der Pflanze folgen. Es kann nicht einfach eine will­kürlich gewählte Spirale zugrunde gelegt werden. Bei Pflanzen ist jede Spiral­kurve einzig­artig und spiegelt die Energie­zufuhr durch die Sonnenein­strahlung sowie die Nähr­stoffe aus dem Boden wider.

Die Spiralen passen sich dabei in der Krümmung k bei den einzelnen Kurven­segmenten nur im 1/100 Bereich an. Im Grunde sind das äußerst gering­fügige Verände­rungen, wie sie in der Natur bei jeder Pflanze durch das tägliche Wachstum beeinflusst werden. Aber die Inter­pretation hat gravierende Folgen auf die grafische Darstellung.

Obwohl in obiger Grafik jeweils die gleiche Spiral­kurve im exakt gleichen Teilungs­winkel angeordnet wurde, sieht man gering­fügige Unter­schiede, die sich aus dem jeweiligen Zell­wachstum ergeben. Um diesen Effekt zu verdeut­lichen, wurden die einzelnen Spiral­kurven bewusst „nicht” individuell angepasst.

Aus dieser Darstellung wird eines deutlich: Möchte man dynamische Prozesse, wie sie zum Beispiel bei einer Galaxie auftreten, anhand von Spiral­kurven unter­suchen, müssen zusätzlich noch weitere Faktoren wie Rotations­geschwindigkeit und die Wirbel­dynamik, hervor­gerufen durch die inneren Wirbel­strukturen, mit einbezogen werden. Ohne sich dessen bewusst zu sein, bewegen wir uns dann ganz schnell im 4-dimensionalen Raum.

⇦ Kapitel Kapitel ⇨