Albert Einstein soll sich einmal gefragt haben, „wie ist es möglich, dass die Mathematik unser sichtbares Universum so gut beschreibt?”
In der Natur spielen Zahlen offensichtlich eine große Rolle. Greifen wir zum Beispiel die Blumen heraus. Es gibt viele Blumen die 3 Blütenblätter haben oder 5. Manche von ihnen haben 34 oder 55. Diese Zahlen kommen sehr häufig vor. Das mag auf den ersten Blick nur nach zufälligen Zahlen aussehen. Aber sie gehören alle zu der sogenannten Fibonacci-Folge.
Leonardo da Pisa (Fibonacci) gilt als einer der bedeutendsten Mathematiker des Mittelalters. Er hatte seinen Höhepunkt des Schaffens zu Beginn der ersten Hälfte des 13. Jahrhunderts. Auf seinen Reisen nach Afrika, Byzanz und Syrien machte er sich mit der arabischen Mathematik vertraut und verfasste mit den dabei gewonnenen Erkenntnissen im Jahre 1202 das Rechenbuch Liber abbaci (Überarbeitung 1228). Aus diesem Buch kennen wir heute vor allem die nach ihm benannte „Fibonacci-Folge”.
Abb. 1: Leonardo da Pisa (Fibonacci)(CC BY-SA 4.0)
Dabei handelt es sich um eine von ihm entwickelte Zahlenreihe, die sich in der Natur widerspiegelt. Er war allerdings nicht der erste, dem diese Folge aufgefallen ist, denn sie war schon in der Antike sowohl den Griechen als auch den Indern bekannt.[1]
Bei dieser Zahlenreihe beginnt man mit den Zahlen 1 und 1. In der weiteren Folge addiert man anschließend immer die beiden letzten Zahlen.
1 + 1 = 2 ... 1 + 2 = 3 ... 2 + 3 = 5 ... 3 + 5 = 8 ... usw.
Die Fibonacci-Folge stellt sich daher wie folgt dar:
1 - 1 - 2 - 3 - 5 - 8 - 13 - 21 - 34 - 55 - 89 - 144 - 233 ...
Heute wird in dieser scheinbar beliebigen Zahlenreihe der Schlüssel für alles Mögliche gesehen. Beginnend mit den Proportionen eines Menschen bis hin zum Aktienmarkt. Es spricht viel dafür, dass die Natur eine Vorliebe für diese Zahlen hat. Aber warum ist das so? Im vorherigen Kapitel und in den nachfolgenden wird aufgezeigt, dass nicht nur der Goldene Schnitt, sondern auch der Goldene Winkel, ja selbst Die Goldene Spirale, eng mit dieser Zahlen-Folge verbunden ist.
Die Fibonacci-Zahlen lassen sich deutlich in der Anzahl von Blütenblättern
ablesen. Besonders häufig findet man sie bei Gänseblümchen. Und statistisch
gesehen treten diese Zahlen in der Botanik sehr häufig auf. Ist uns schon einmal
aufgefallen, dass viele Pflanzen spiralförmig wachsen? Wenn man sich zum Beispiel
einen Tannenzapfen von schräg unten anschaut, erkennt man spiralförmige
Linien zwischen den Samenschuppen. Oder die Schuppen einer Ananas, sie laufen in
Besonders eindrucksvoll sind diese Zahlenverhältnisse am Beispiel der
Sonnenblume zu erkennen. Der gesamte Blütenkorb besteht aus zahlreichen
kleinen Blüten, die sich später zu Samen ausbilden. Diese sind jedoch nicht chaotisch
angeordnet, sondern man kann deutlich rechtsdrehende und linksdrehende
Spiralzüge erkennen. Selbst die Anzahl der Spiralzüge ist nicht
willkürlich, denn bestimmte Zahlen treten immer wieder auf. Man kann oft
55 und 89 sich kreuzende Spiralen erkennen,
manchmal sogar mehr. Die jeweilige Anzahl dieser Spiralen entspricht in der Regel einer
Fibonacci-Zahl. Und zählt man die Spiralen, die in entgegengesetzter Richtung
verlaufen, erhält man eine benachbarte Fibonacci-Zahl. Bei sehr großen
Sonnenblumen findet sich oftmals ein Verhältnis von 89 : 144
oder sogar



Weitere Untersuchungen haben gezeigt, dass die Fibonacci-Folge noch zahlreiche andere Wachstumsvorgänge der Pflanzen beschreibt. Auf eine sehr simple geometrische Weise setzen die Pflanzen einen Mechanismus in Gang, der in vielen Fällen die Fibonacci-Folge erzeugt. Es scheint, als wenn sie eine Art Wachstumsmuster in der Natur ist. Die Fibonacci-Folge beschreibt interessanterweise sogar das Wachstum von Schneckengehäusen oder, man mag es kaum glauben, selbst das Wachstum einer Kaninchenpopulation.[2]
Aufgrund der Beziehung zur vorherigen und zur nachfolgenden Zahl scheint Wachstum und Fortpflanzung in der Natur einem Additionsgesetz zu folgen. Jede Zahl hat eine Beziehung zur vorherigen Zahl und zur nachfolgenden Zahl. Ähnlich wie Major eine Beziehung zu Minor und dem Ganzen beim Goldenen Schnitt hat. Die Fibonacci-Folge steht somit, wie bereits erwähnt, in einem unmittelbaren Zusammenhang zum Goldenen Schnitt.
Je weiter man in der Folge fortschreitet, desto mehr nähert sich der Quotient
aufeinanderfolgender Zahlen dem Goldenen Schnitt
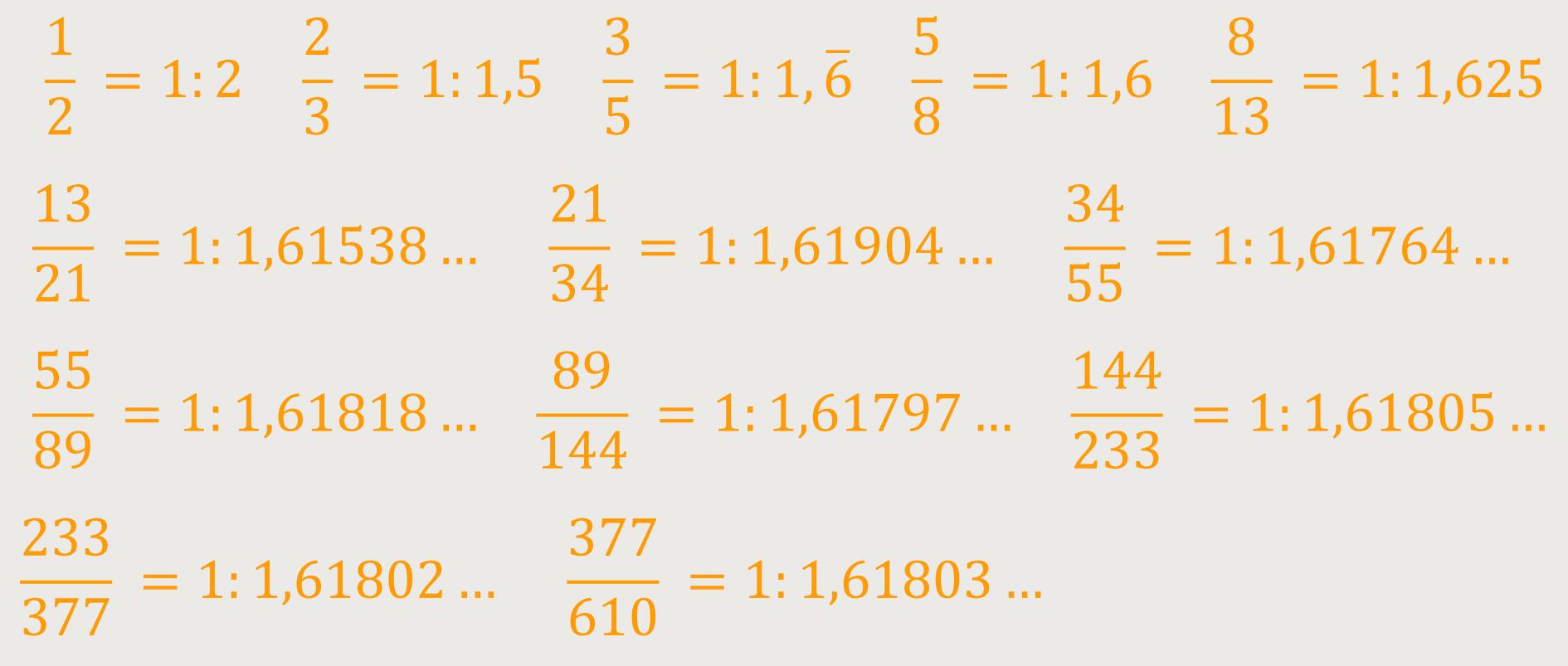
Diese Annäherung ist alternierend, das heißt die Quotienten sind abwechselnd kleiner und größer als der Goldene Schnitt bzw. Der Goldene Winkel. [3]
Am nachfolgenden Beispiel kann man schön erkennen, wie zwei beieinanderliegende Zahlen aus der Fibonacci-Folge ein harmonisches Spiralmuster ergeben. Dabei geht es nicht nur um die Ästhetik wie beim Goldenen Schnitt, sondern eine solche Anordnung beinhaltet die effizienteste Flächenausnutzung für eine maximal mögliche Blütenzahl und damit eine beste Samenausbeute. Nachfolgende vereinfachte Darstellung zeigt dies anschaulich:
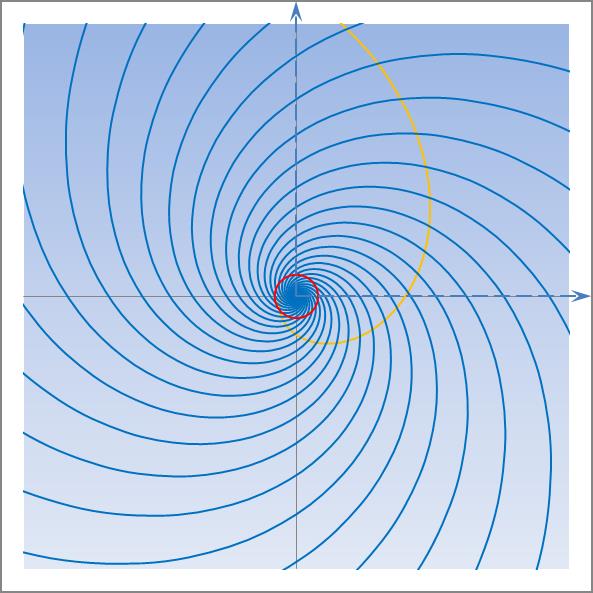
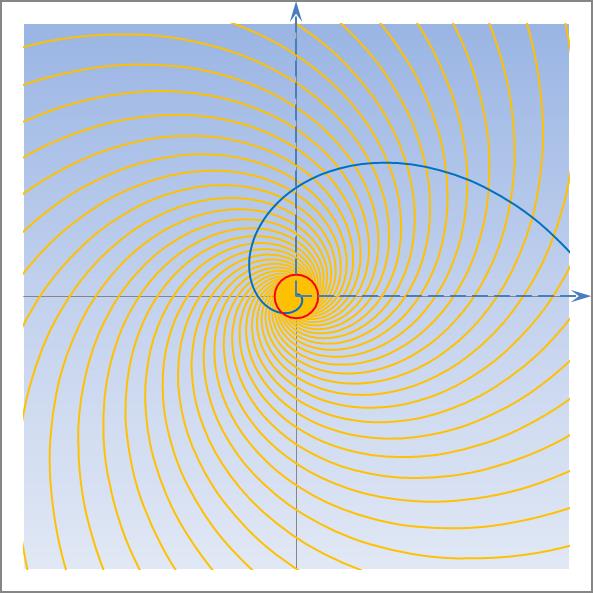
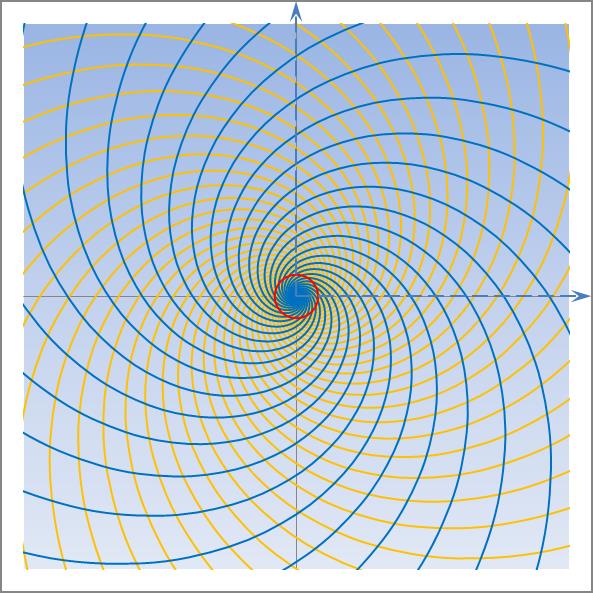
Je mehr Spiralzüge das betrachtete Objekt aufweist, umso exakter wird das Verhältnis des Goldenen Schnitts. Und das heißt wiederum, je exakter das Verhältnis zweier aufeinander folgender Fibonacci-Zahlen, desto mehr nähert sich das Verhältnis der Naturkonstanten Φ (Phi) an.
Aber warum wachsen Pflanzen in Spiralen? Hat es irgendeine Bewandtnis mit der Anzahl der Spiralen? Und warum kann man ähnliche Spiralmuster auch bei den Galaxien erkennen? Dazu später mehr.
Zunächst möchten wir die Einzigartigkeit der Maßzahl des Goldenen Schnitts, auch besser bekannt als die Naturkonstante Φ (Phi) im Detail näher beleuchten.
Quellen
[1] Parmanand Singh: The So-called Fibonacci numbers in ancient and medieval India. In: Historia Mathematica. 12, Nr. 3, 1985, S. 229-244.[2] Ruben Stelzner (in Zusammenarbeit mit Wolfgang Schad): Der Goldene Schnitt. Das Mysterium der Schönheit. In: golden-section.eu.
[3] (Beutelspacher & Petri 1995)
⇦ Kapitel Kapitel ⇨

