Die Zahlen-Folge nach Fibonacci weist, wie wir gesehen haben, einige bemerkens­werte mathe­matische Besonder­heiten auf. Zum einen ist es die Zahl Φ (Phi) selbst.

Die Maßzahl des Goldenen Schnitts und des Goldenen Winkels gehört zu den irratio­nalen Zahlen, das heißt sie ist nicht durch einen Bruch ganzer Zahlen dar­stellbar, wie zum Beispiel 1/3. Zu diesen irratio­nalen Zahlen gehören unter anderem die Kreis­zahl π (pi) und die Zahl, die sich aus der √2 ergibt. Nun scheint es, als wären alle irratio­nalen Zahlen gleich irrational, aber tatsäch­lich sind einige irrationaler als andere.

Die irrationalen Zahlen lassen sich quasi in verschie­denen Stufen der Irratio­nalität beschreiben. In einer Aufzäh­lung der irratio­nalen Zahlen bildet die Goldene Zahl Φ (Phi) das Schluss­licht. Φ (Phi) ist die irratio­nalste aller irrationalen Zahlen. Das wirkt erst einmal erstaun­lich, denn es besagt nichts anderes als, dass wir gerade das Irratio­nalste als besonders harmonisch empfinden.

Und das ist wirklich außer­gewöhn­lich. Rational betrachtet ist das, was wir als extrem wohl­propor­tioniert empfinden, etwas völlig Gegen­sätz­liches. Eine mathe­matische Betrachtung der Zahl Φ (Phi) macht ihre Einzig­artigkeit deutlich. So lassen sich die Verhältnis­mäßig­keiten der drei Größen „Minor”, „Major” und „das Ganze” in einer einfachen Beziehung darstellen. Die bisher bekannteste Formel lautet:

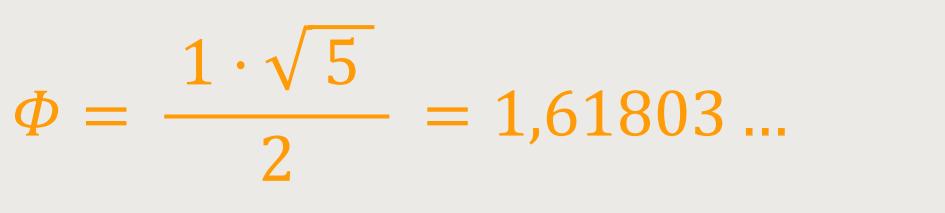
Es gibt noch eine weitere Formel, die selbst unter Mathe­matikern nicht so verbreitet sein soll. Jeder mathe­matische Bruch lässt sich bekannt­lich als sogenannter Ketten­bruch dar­stellen. Beim Ketten­bruch wird das Verhältnis simpli­fiziert, indem man den ursprüng­lichen Bruch in einfachere Brüche auf­gliedert. Zähler jedes einzelnen Bruches ist die Zahl Eins. Zum Beispiel lässt sich ein rationales Verhältnis wie folgt darstellen:

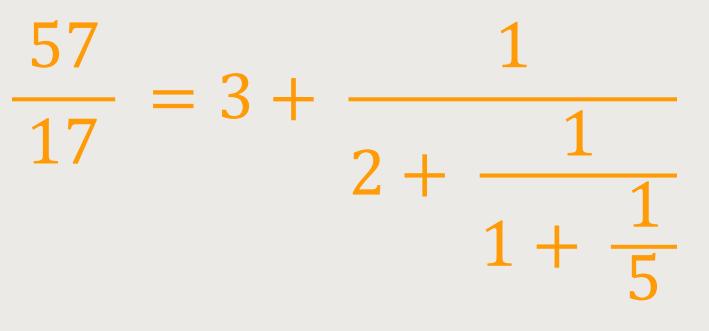
Neben den Bruch­zahlen lassen sich auch irrationale Zahlen durch einen Ketten­bruch darstellen. Der einzige Unter­schied besteht darin, dass der Ketten­bruch einer irrationalen Zahl unendlich ist.

Insofern lässt sich die Kreiszahl π (pi) wie folgt darstellen:

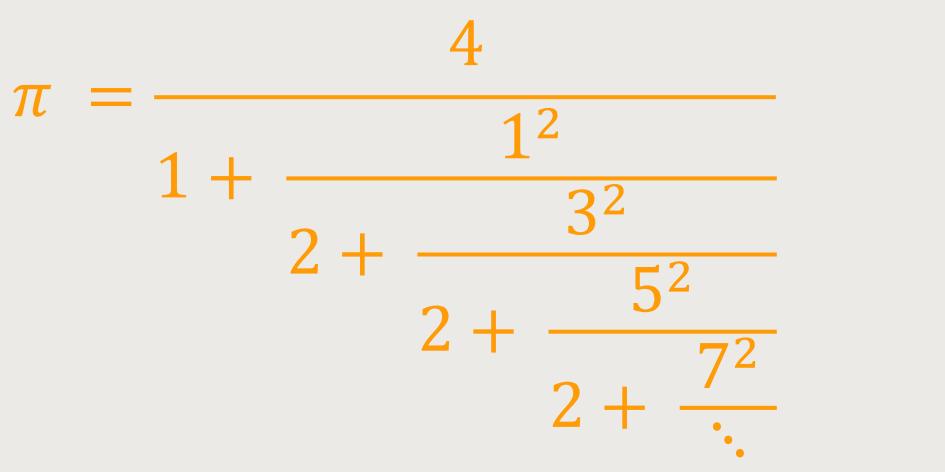
Andererseits lässt sich √2 wie folgt charakterisieren:

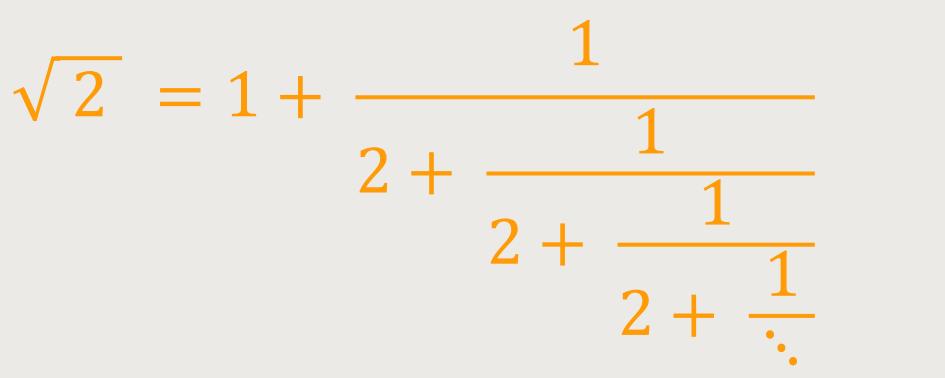
Auch die irrationale Zahl Φ (Phi) lässt sich in Form eines Kettenb­ruches darstellen:

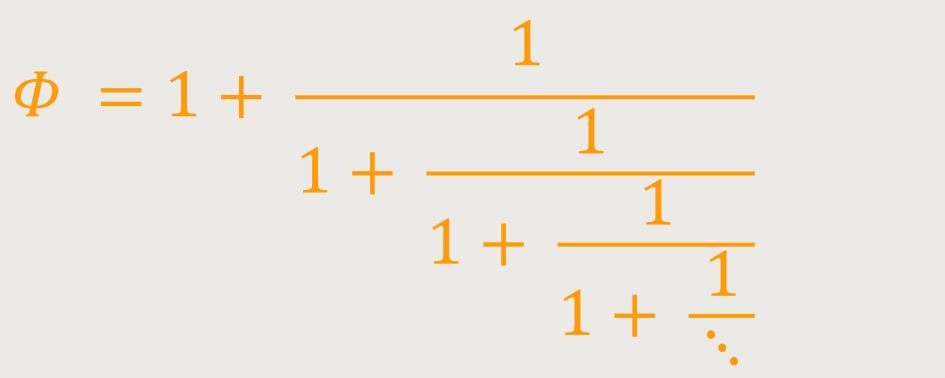
Der Ketten­bruch zur Berechnung der Zahl Φ (Phi) nimmt aller­dings eine Sonder­stellung ein, weil er sich als einziger mit nur einer Zahl darstellen lässt. Der Goldene Schnitt errechnet sich tatsäch­lich nur aus der Zahl Eins. Das Ein­fachste ist somit Aus­druck des Irratio­nalsten. Die Natur bevorzugt dieses Verhält­nis in zahl­losen Erscheinungs­formen. Es spricht viel dafür, dass dieses ver­schachtelte und zugleich minimalis­tische Additions­prinzip Natur­prozesse visualisiert, die wir bisher noch nicht völlig verstanden haben.

Eine zweite Ableitung der Zahl Φ (Phi) sieht wie folgt aus:

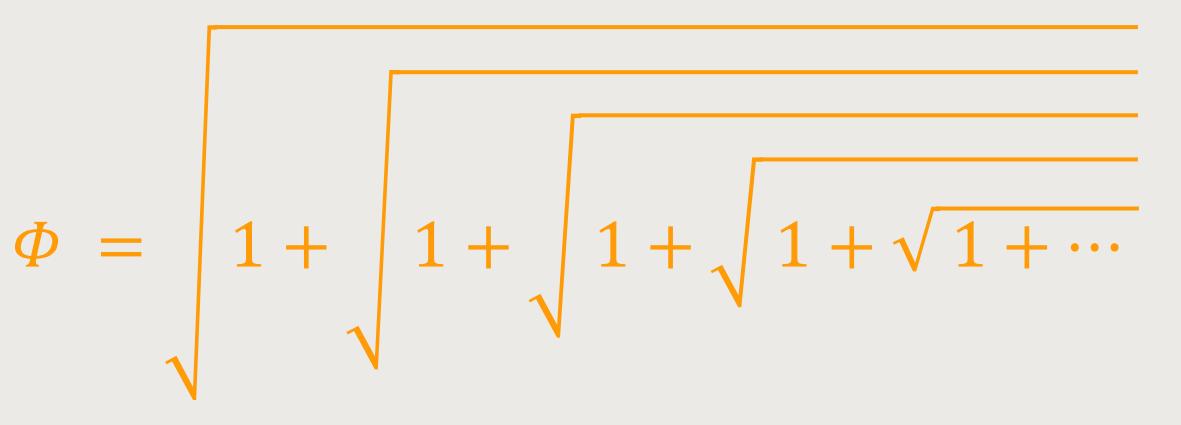
Diese zweite Ableitung gleicht etwas mehr der geome­trischen Ausdrucks­weise des Goldenen Schnitts. So wie „Minor” eine Beziehung zum „Major” hat, so hat auch in obiger Formel jedes Element eine Beziehung sowohl zum über­geordneten als auch zum unter­geordneten Element. Gerade das Verhältnis des „Ganzen” und seiner unter­geordneten Teile zueinander beschreibt anschaulich den Goldenen Schnitt, der sich indirekt hier wiederfindet.

Die mathematischen Ausführungen zeigen auf eindrucks­volle Weise, dass der Goldene Schnitt, der Goldene Winkel, die Fibonacci-Folge, ja selbst die Zahl Φ (Phi) eine „unbezweifel­bar zentrale Rolle inner­halb der Mathe­matik” einnehmen. Im Grunde beschreiben sie alle ein und dasselbe Phänomen.

Bisher ging man davon aus, dass die heraus­ragende Stellung der Zahl Φ (Phi) in der Mathe­matik ein ungeklär­tes Rätsel ist. Und dass sich aus der mathe­matischen Analyse allein keine Erklärung finden lässt. Letzt­lich geht es auch darum, den inhalt­lichen Charakter und dessen Aussage­kraft zu ergründen. Die mathe­matischen Zusammen­hänge können jedoch helfen, die Verbindung zum universalen Charakter der Proportio divina und damit zur Schön­heit der Schöpfung zu finden. Carl Friedrich von Weizsäcker soll einmal gesagt haben: „Vielleicht ist die allgegenwärtig verborgene Mathematik der Natur der Seinsgrund aller Schönheit.” (von Weizsäcker 1995)

Es erhebt sich daher die Frage, wenn letzt­lich auch die Fibonacci-Folge den Mechanis­mus der Pflanzen oder anderer Lebe­wesen so erstaun­lich zu beschreiben scheint, was fehlt uns noch, um den Code endgültig zu entschlüsseln? Um das Bild zu vervoll­ständigen kommen wir nicht umhin, auch kurz den Golden Winkel zu betrachten.

⇦ Kapitel Kapitel ⇨