Wir erinnern uns, der Goldene Schnitt beschreibt das Ver­hältnis von „Minor” zu „Major” mit einem Verhältnis von 1 : 1,61803....

Wir konnten bereits sehen, dass diese Maß­zahl, die auch als Natur­konstante Φ (Phi) bezeichnet wird, sich aus der Fibonacci-Folge ableiten lässt. Aber wie lässt sich der Zusammen­hang zwischen dem Goldenen Schnitt und dem Goldenen Winkel im Detail visualisieren?

Hierzu denkt man sich einen Voll­kreis von 360°. Bei 12 Uhr beginnend, teilt man gegen den Uhrzeiger­sinn einen Winkel von 137,5° ab. Damit ergibt sich ein Rest­winkel von 222,5°. Das Ver­hältnis der beiden Winkel zueinander (137,5°/222,5°) beträgt annähernd 1 : 1,61803.... Da dies genau dem Goldenen Schnitt ent­spricht, bezeich­net man den Winkel von 137,5° verständlicher­weise auch als den Goldenen Winkel.

Jetzt könnte man den gleichen Voll­kreis, wieder bei 12 Uhr beginnend, in jeweils gleich große Stücke unterteilen, wobei die Teilung einer der Zahlen aus der Fibonacci-Folge ent­sprechen muss. Nun kann man fest­stellen, dass beispiels­weise bei 13 gleich großen Stücken, 8 Teilstücke im Bereich der 222,5° liegen und 5 Teilstücke im Bereich der 137,5°.
Oder würde man den Voll­kreis in 55 gleich große Stücke unter­teilen, erhält man 34 Teilstücke im Bereich der 222,5°, und 21 Teilstücke liegen im Bereich der 137,5°.
Die Gesamtzahl teilt sich somit in zwei Anzahlen auf, die jeweils den Zahlen der Fibonacci-Folge ent­sprechen. Unter anderem kann man erkennen, dass die Auswahl der Zahlen, wie bereits ange­sprochen, einem Additions­prinzip folgt.

Je größer die Gesamt­zahl der gleich großen Teil­stücke ist, desto genauer wird das Ver­hältnis zwischen den beiden Teil­abschnitten (225,5°/137,5°), und desto genauer wird der Goldene Winkel. Letzt­lich kann man den Goldenen Schnitt mit 1,61803... angeben und den Goldenen Winkel mit 137,507764...°.

Die anschließende Grafik zeigt sehr schön, wie sich die Blatt­anordnung bei einer unter­schiedlichen Gesamt­zahl darstellt. Zur besseren Sicht­barkeit wurde die jeweilige Blatt­anordnung farblich anders abgesetzt.

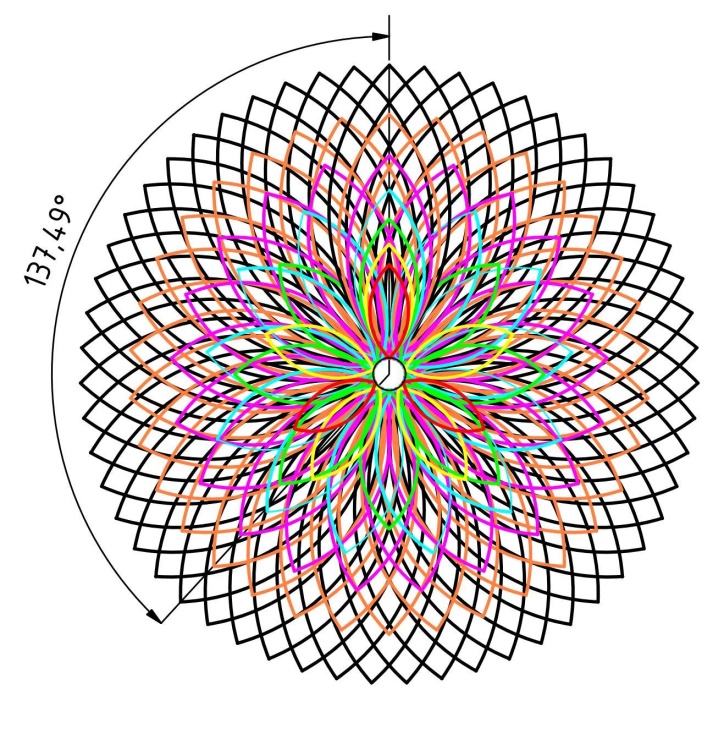
Abb.1: Bei 55 Blütenblättern (schwarz) beträgt der Goldene Winkel ca. 137,49...°

Die Goldene Spirale ist ein Sonder­fall der Logarith­mischen Spirale. Diese Spirale lässt sich mittels rekursiver Teilung eines „Goldenen” Recht­ecks in je ein Quadrat und ein weiteres, kleineres „Goldenes” Recht­eck konstru­ieren. Sie wird oft durch eine Folge von Viertel­kreisen auf Grund­lage der Fibonacci-Folge approxi­miert. Ihr Radius ändert sich bei jeder 90°-Drehung um den Faktor Φ .

Eine vereinfachte Dar­stellung der Goldenen Spirale entspricht somit der Fibonacci-Folge.

Bei nachfolgender Grafik wurden die Zahlen

aus der Fibonacci-Folge zugrunde gelegt. Man kann einen Kurven­verlauf erkennen, der sehr einer Logarith­mischen Spirale ähnelt.

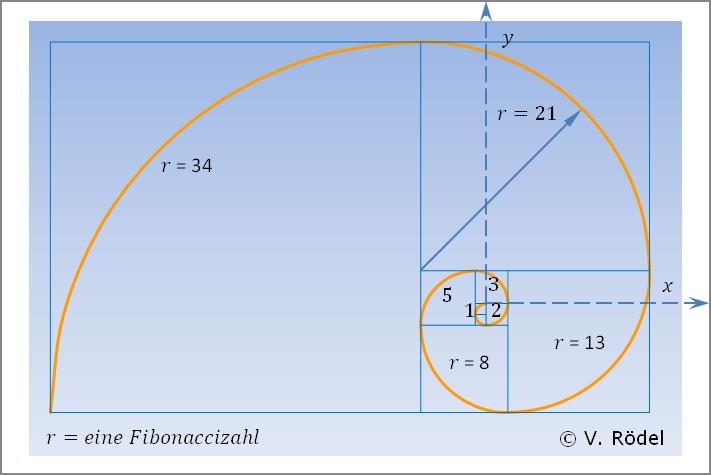
Abb. 2: Fibonacci-Folge (rechtsdrehend)

Die Polardarstellung der Goldenen Spirale ist definiert als:

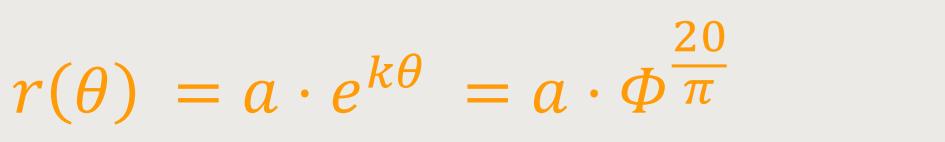
Die Steigung k ist definiert als:

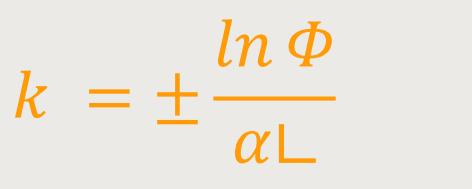
α∟ ist der Zahlen­wert für den rechten Winkel, also 90° oder π/2.

Insofern lässt sich auch schreiben:

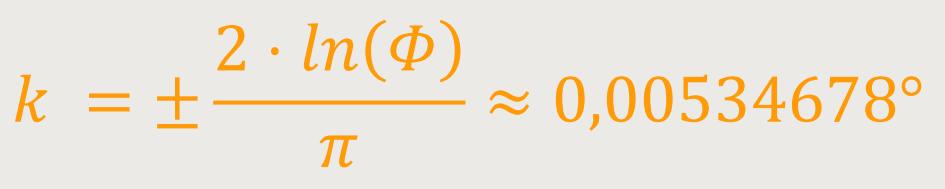
Hierbei ist:

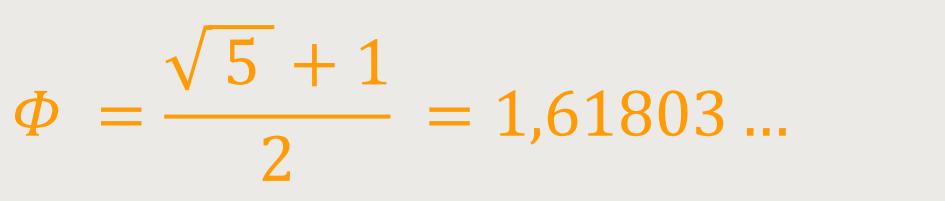
Bei der grafischen Dar­stellung der realen Goldenen Spirale basie­rend auf der irratio­nalen Zahl Φ (Phi) verläuft der Kurven­verlauf fast analog.

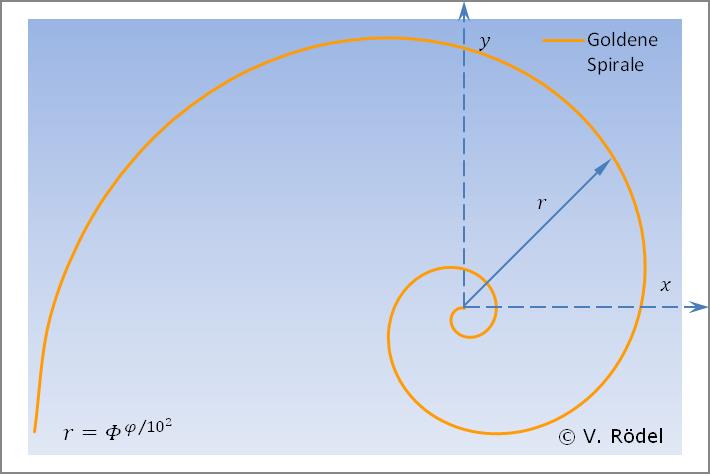
Abb. 3: Goldene Spirale (rechtsdrehend) basierend auf Φ (Phi)

Die Polardar­stellung der realen Goldenen Spirale ist definiert als:

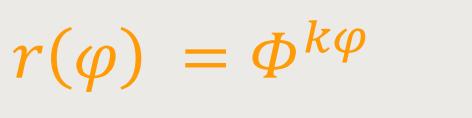
Die Steigung k ist definiert als:

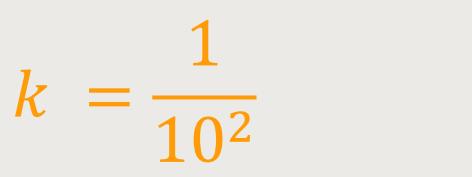
Daraus folgt durch einsetzen:

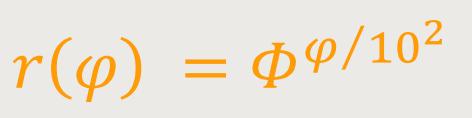
Wie wir später noch sehen werden, hat diese Schreib­weise einen enormen Vorteil.

Eine direkte Gegen­über­stellung beider Spiralen zeigt eine erstaun­liche Ähnlich­keit.

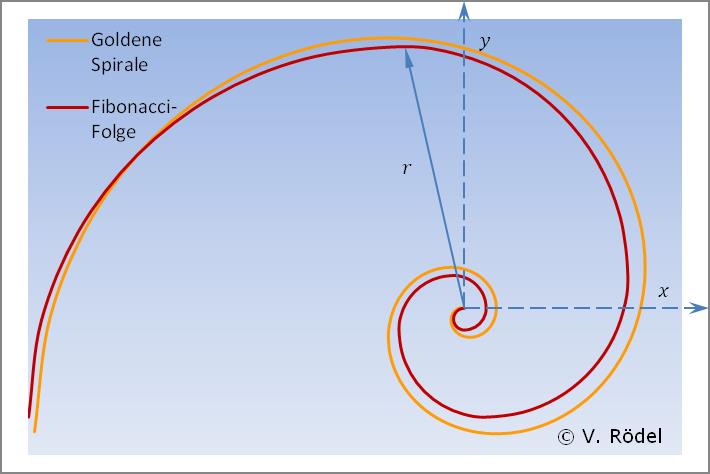
Abb. 4: Gegenüberstellung der Goldenen Spirale mit der Fibonacci Folge

Hierbei gilt analog wie oben:

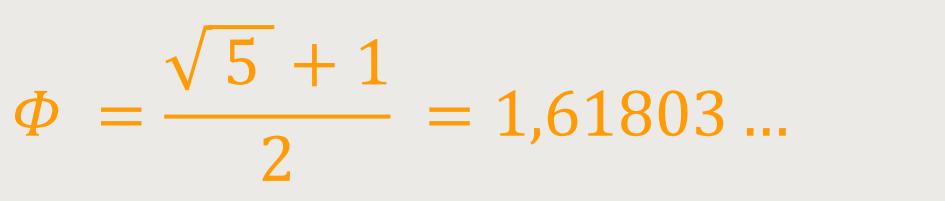
Bei der grafischen Dar­stellung der realen Goldenen Spirale, basierend auf der irratio­nalen Zahl Φ (Phi), ist der Kurven­verlauf homogener.

Man kann ohne Weiteres eine Ähnlich­keit zwischen den beiden Varianten, der Goldenen Spirale und der Fibonacci-Folge, erkennen. Damit zeigt sich, dass sich eine Approxi­mation mittels Fibonacci-Folge anbietet, um den Kurven­verlauf der Goldenen Spirale verein­facht darzustellen.

Soweit so gut, aber jetzt entsteht ein gravie­rendes Problem. Sowohl die Goldene Spirale als auch deren Approxi­mation beginnen im Koordinaten­ursprung bei (0|0). In der Natur wächst aber nichts ausgehend von einem Null-Zustand. Nichts hat eine poten­tielle Energie, die dem Wert Null entspricht.

Wir müssen vielmehr einen Bereich zugrunde legen, beginnend mit der Größe der kleinsten Moleküle, bis hin zum genetisch fest­gelegten maximal mög­lichen Wachstums­stadium einer Pflanze. Somit können wir bei unseren Über­legungen nicht von Null aus­gehen. Und streng genommen können wir selbst den Grenz­wert ± ∞ nicht vor­behaltlos einsetzen.

Des Weiteren muss der Kurven­verlauf bzw. die Krümmung der Kurve etwas flacher verlaufen und zudem um den Ursprung „spiralen”. Und damit betrachten wir im weiteren Verlauf Spiral­kurven, wie sie auch in der Natur auf mannig­faltige Weise vorkommen.

⇦ Kapitel Kapitel ⇨