Die Spezielle Relativitäts­mechanik ist eine konse­quente Weiter­führung der Idee des Relativitäts­prinzips. Dieses Relativitäts­prinzip führt letzt­lich zum Prinzip von der Konstanz der Licht­geschwindig­keit. Und daraus ergeben sich unaus­weichliche Folgerungen, wie die Zeit­dilatation, die Längen­kontraktion und den Verlust der absoluten Gleich­zeitig­keit. Gemäß diesem Prinzip ist die Licht­geschwindig­keit eine Grenz­geschwindig­keit.

Man fragt sich zwangs­läufig, warum das so ist? Wenn eine konstante Kraft auf einen Körper ausge­übt wird, müsste dieser doch immer weiter beschleu­nigt werden können. Demnach müsste es doch mög­lich sein, auch die Licht­geschwindig­keit zu über­schreiten. Zumindest würde aus mecha­nischer Sicht nichts dagegen sprechen.

Dazu gab es ein Experiment beim CERN in Genf. Dort wurde unter­irdisch ein Linear­beschleuniger mit einer Länge von 1 km auf­gebaut, und anschlie­ßend wurden Elek­tronen in einem elek­trischen Feld beschleunigt. Laut der tech­nischen Anforde­rungen sollte der Beschleu­niger in der Lage sein, die Elek­tronen am Ende dieser Weg­strecke von 1 km bis auf eine Geschwindig­keit von 283 · c_₀ zu beschleu­nigen. Man hat diese Elek­tronen parallel mit Licht­signalen laufen lassen, und abge­sehen von einer geringen Fehler­quote hatten beide tatsäch­lich nahezu die gleiche Lauf­zeit. Das hatte man aus Sicht der klassischen Physik nicht erwartet.

Warum wird ein Elektron nicht noch schneller, wenn es doch durch derart hohe Spannungen über eine lange Strecke beschleu­nigt wird? Es muss wohl daran liegen, dass sich diese massiven Körper bei Heran­nahen an die Licht­geschwindig­keit immer stärker einer weiteren Beschleunigung ihrer selbst wider­setzen. Offen­sichtlich erhält der Körper eine immer größere Träg­heit.

Denn die träge Masse ist ein Parameter der beschreibt, wie stark sich ein Körper der Beschleu­nigung seiner selbst wider­setzt. Diese träge Masse ist auch stets propor­tional zur schweren Masse, einem Parameter der beschreibt, wie stark eine Masse von einer anderen ange­zogen wird. Aber das ist im Rahmen der Speziellen Relativitäts­mechanik weitest­gehend ohne Belang.

In der Allge­meinen Relativitäts­mechanik allerdings ist es möglich, auch die Bewe­gungen von massiven Körpern unter dem Ein­fluss der Gravitations­wechsel­wirkungen auf Träg­heits­bewegungen zurück­zuführen. Dabei ist es jedoch not­wendig von einer 4-dimensionalen Raum­zeit zu sprechen, die zusätz­lich noch gekrümmt ist.

Der Tensor­formalismus erlaubt es dann, die Gesetz­mäßig­keiten, die für 2-dimensionale Flächen gelten, auf höher­dimensionale Mannig­faltig­keiten zu verall­gemeinern.

Und so sind zum Beispiel die Diagramme der Lorentz-Trans­formation ledig­lich 2-dimensionale Aus­schnitte aus einer 4-dimensionalen Raum­zeit. Um ein Ereignis in Raum und Zeit fest­zulegen, benötigt man eine solche 4-dimensionale Raum­zeit, und das wird im Rahmen der Speziellen Relativitäts­mechanik auch als der Minkowski-Raum bezeichnet.

Es muss wohl so sein, dass diese massiven Körper, wie beispiels­weise die Elektronen, bei einer Beschleu­nigung ihrer selbst eine immer größere träge Masse erhalten. Auf­grund dessen kann die Licht­geschwindig­keit weder erreicht und schon gar nicht über­schritten werden.

Wenn es um die Masse eines bewegten Körpers geht, führt man als Begriff eine soge­nannte dynamische Masse ein. Diese dynamische Masse ist gleich der Masse die der Körper hat, wenn er sich nicht bewegt, dividiert durch die bereits bekannte Wurzel für Grenz­geschwindig­keit des Lichts.
Und damit wird die dynamische Masse definiert als:

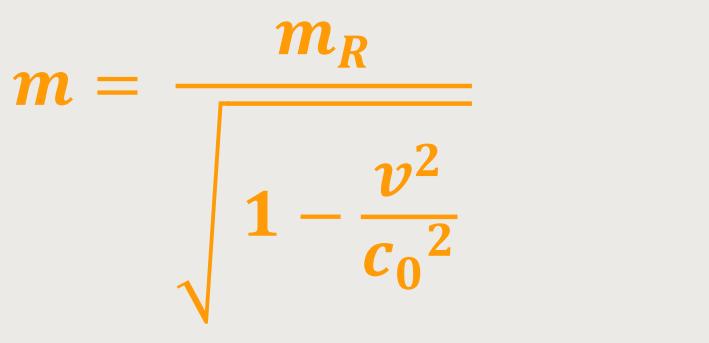
m_R   ist die Masse des ruhenden Körpers

Somit ist die dynamische Masse eines bewegten Körpers immer größer als die in einem Ruhe­system gemessene Masse.

Wenn zum Beispiel Elektronen mit bekannter Geschwindig­keit in elek­trischen und magne­tischen Feldern abge­lenkt werden (siehe Lorentz-Kraft), dann lässt sich bei einem solchen Elektronen­strahl beobachten, dass sich die Bahn bis zu einem Kreis und sogar bis hin zu einer Schrauben­linie ausbildet.

Bei bekannter Beschleu­nigungs­spannung und bekanntem Magnet­feld lässt auf diese Weise die Elementar­ladung e /m_e definieren und damit die Masse eines Elektrons bestimmen. Die Masse wird bei immer höheren Geschwindig­keiten entspre­chend verän­dern. Wenn­gleich deren Wert immer noch deut­lich geringer aus­fällt, als die Masse eines Protons oder Neutrons.

Bei der Beschleu­nigung eines Elektrons wird ständig Arbeit geleistet.

In der klassischen Physik wird die kinetische Energie definiert als:

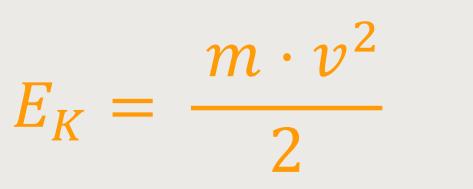
In diesem Fall ent­spricht es der Arbeit, die hinein­gesteckt wird, um diesen Körper in einem Inertial­system von der Anfangs­geschwindig­keit Null auf die Geschwindig­keit v zu beschleu­nigen. Die kinetische Energie wird sozu­sagen dem Körper zuge­eignet.

Bei der relativis­tischen Betrachtung sieht es etwas anders aus.

Um die Über­legung etwas anschau­licher zu machen, sei die Geschwindig­keit v um einiges kleiner als die Licht­geschwindig­keit c_₀. Dann gilt zunächst für die dynamische Masse wie oben definiert:

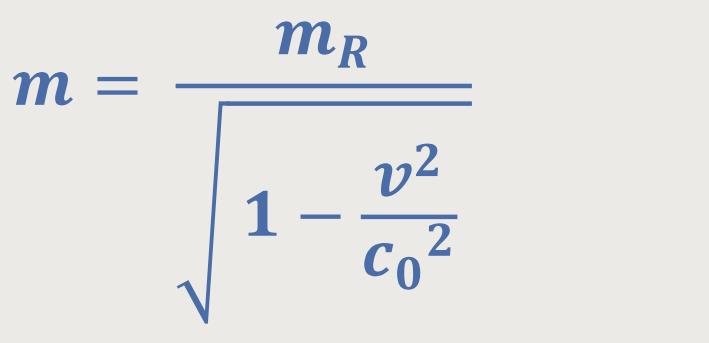
Da dieses v² / c_₀² jetzt sehr klein sein soll gegen 1, kann man eine Verein­fachung durch­führen. Durch entspre­chende (Potenz)-Rein­entwick­lungen lässt sich zeigen, dass für ε ≪ 1 folgendes gilt:

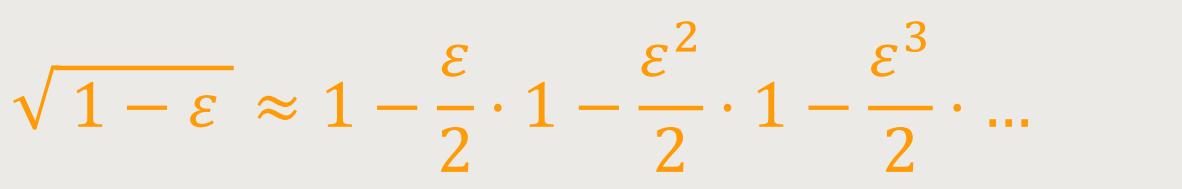
Anderer­seits gilt:

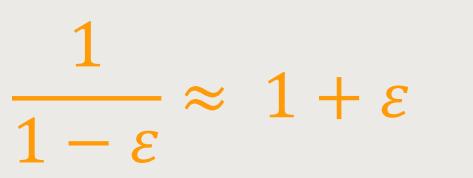
Wenn man diese beiden Nähe­rungs­regeln zugrunde legt, ergibt sich jetzt für die dynamische Masse durch Einsetzen der ersten Regel:

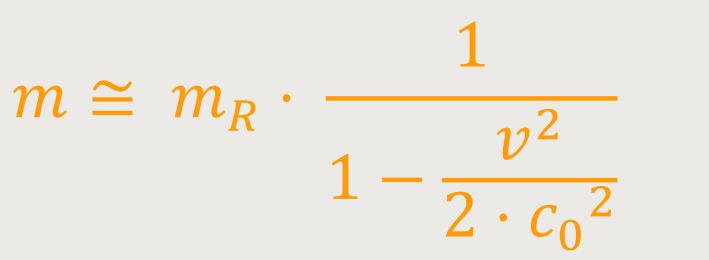
Und durch Einsetzen der zweiten Regel ergibt sich weiter:

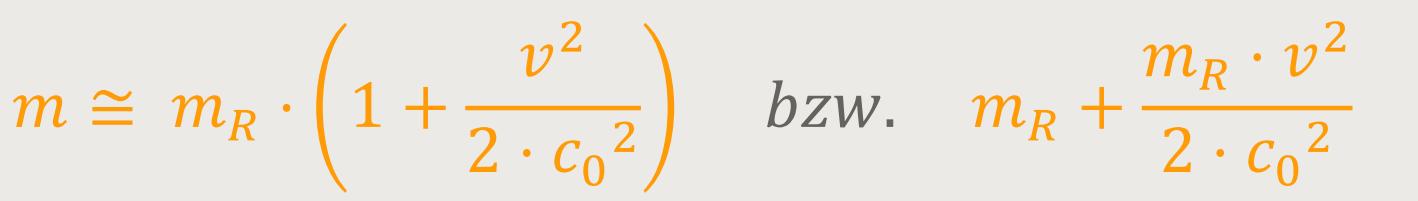
Das ähnelt sehr der Definition der kinetischen Energie (s.o.) und durch Umformung erhält man:

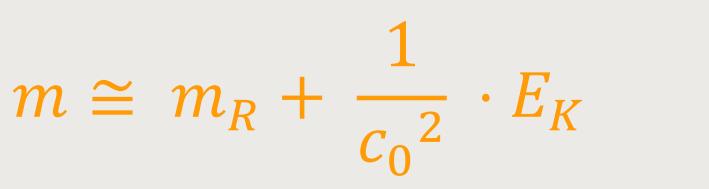
Durch noch­malige Umformung erhält man abschlie­ßend für die kinetische Energie eines Teilchens mit der Geschwindig­keit v:

Man erkennt, dass die kinetische Energie, die der Körper aufnimmt, wenn er sich mit der Geschwindig­keit v bewegt, ausge­drückt werden kann durch die Verän­derung seiner Masse, in diesem Fall eine Massen­zunahme, multi­pliziert mit der Licht­geschwindig­keit zum Quadrat.

Diese Beziehung gilt nicht nur bei niedrigen Geschwindig­keiten, sondern auch im all­gemeinen Fall.

Grafik (wird später eingefügt)

Die dynamische Masse eines bewegten Körpers macht sich bei moderaten Geschwindig­keiten kaum bemerk­bar. Wenn sich die Geschwindig­keit aller­dings Richtung Licht­geschwindig­keit bewegt, nimmt die Masse rapide zu, quasi hyperbo­lisch. Man kann damit auch von einer Äqui­valenz von Masse und Energie sprechen.

Um die Masse eines Körpers um einen Betrag Δm zu erhöhen, ist eine entspre­chende kinetische Energie E_K erforderlich:

Im Umkehr­schluss ergibt sich daraus, wird die Masse um Δm gesenkt, dann wird die gleiche Energie wieder frei.

In unserem Alltag bedeutet das zum Beispiel, dass ein Energie­verbrauch von 1 kWh einer Massen­veränderung von 4×10⁻¹¹ kg ent­spricht. Deshalb merken wir davon im Alltag nichts. Aber um wie viel kann die Masse eines Körpers gesenkt werden? Zunächst würde man denken, Schluss ist bei der Ruhe­energie. Denn Ausgangs­punkt war ja die Ruhemasse.

Grafik

Aber Experimente weisen darauf hin, dass Teilchen ihre Masse auch komplett verlieren können. Zum Beispiel, wenn ein Proton und ein Antiproton zusammen­stoßen. Die sind zwar nur in sehr kleiner Zahl vor­handen, aber wenn trotz­dem ein der­artiger Zusammen­stoß beispiels­weise in einer Beschleu­nigungs­anlage erfolgt, dann kommt es zu einem großen Crash. Und deren Masse wird umge­wandelt, wobei ein großer Licht­blitz ent­steht, sprich es werden Gamma­strahlen ausge­sendet. Das sind hoch­energe­tische Photonen.

Auch bei anderen Elementar­teilchen­reaktionen kann es vorkommen, dass vielerlei andere neue Teilchen entstehen können. Das deutet darauf hin, dass mit der Ruhe­masse noch nicht das Ende der Fahnen­stange erreicht ist. Letzten Endes ist es somit möglich, dass die gesamte Masse eines Körpers inklusive seiner Ruhe­masse in Energie umgesetzt werden kann. In diesem Fall spricht man deshalb auch von einer „Ruhe­energie”.

Daraus ergibt sich dann für einen ruhenden Körper mit Ruhe­masse m_R, dass er auch eine Ruhe­energie E_R enthält, woraus folgt:

Und das ist die berühmte Formel von Albert Einstein.

Damit lässt sich letzt­lich die Gesamt­energie eines bewegten Körpers mit einer dynamischen Masse berechnen:

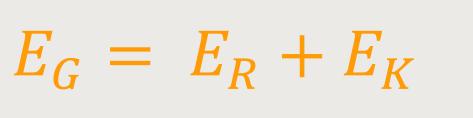
Oder wenn man das, was wir zuvor erarbeitet haben, entspre­chend einsetzt, erhält man:

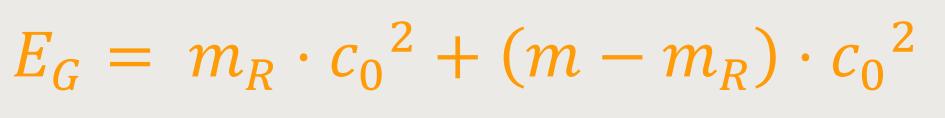
Nach Kürzen bleibt nur mehr übrig:

Damit ent­spricht die Gesamt­energie eines bewegten Körpers der dynamischen Masse multi­pliziert mit der Licht­geschwindig­keit zum Quadrat.

Insofern erhält man zwei unter­schied­liche Bezie­hungen für die Energie eines Körpers. Einmal bezogen auf seine Ruhe­masse und einmal bezogen auf seine dynamische Masse.

Welche Auswirkung hat das nun auf die Erhaltungs­sätze?

Wie wir wissen, ist die Summe der Impulse vor und nach einem Stoß jeweils die Gleiche. Die Summe der Energien vor und nach einem Stoß ist die Gleiche. In der klassischen Mechanik ändert sich beides nicht.

Bei hohen Energien dagegen sieht das für die Impulse wie folgt aus, wenn zwei Teilchen einander stoßen:

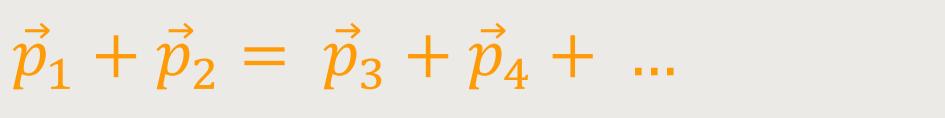
Somit können sich Impulse von neuen Teilchen bilden.

In der klassischen Physik bilden sich solche Schauer von Teilchen nicht. Aber in der Physik der Elementar­teilchen kann es sehr wohl dazu kommen.

Des Weiteren gilt für die Gesamt­energie der Stoß­partner:

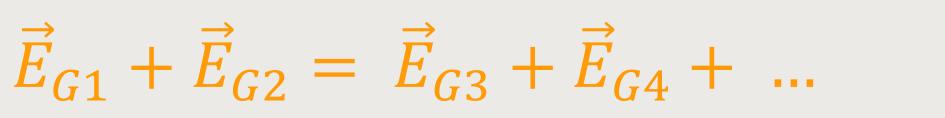
Und damit können sich auch Gesamt­energien von neuen Teilchen bilden.

Wichtig ist aber hierbei zu berück­sichtigen, dass der Impuls grund­sätzlich wie in der klassischen Physik definiert wird:

Aber für das m muss jetzt die dynamische Masse einge­setzt werden, und daher ergibt sich für die relativis­tische Mechanik:

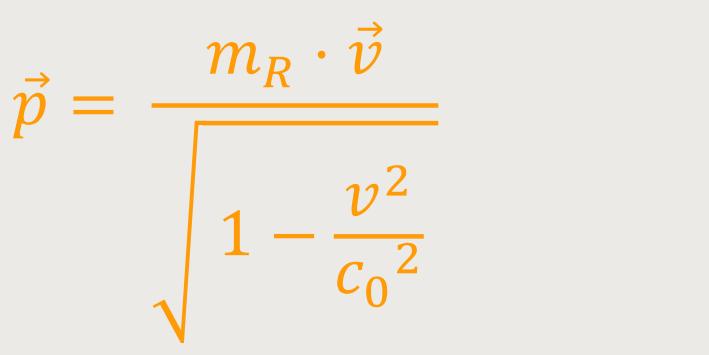
Ähnliches gilt für die Gesamt­energie, die in gemäß der klassischen Physik definiert wird:

Auch hier setzt man für das m wieder die dynamische Masse ein, und daher ergibt sich:

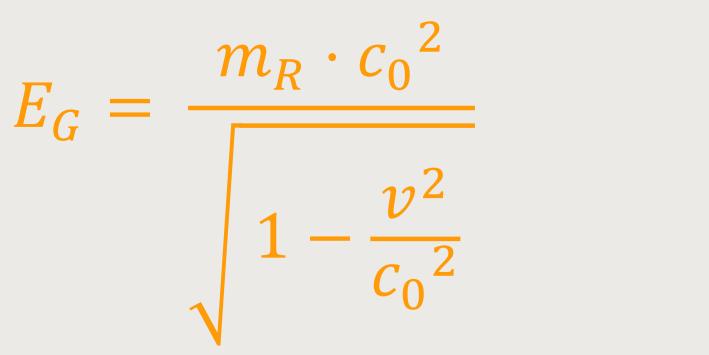
Auf diese Art und Weise bleiben die Erhaltungs­sätze, insbe­sondere für den Impuls und die Energie, auch in der Relativitäts­mechanik gültig.

In neueren Darstel­lungen der Relativitäts­mechanik wird es manch­mal vermieden, den Begriff der dynamischen Masse einzu­führen. So versucht man das Problem mit der Gravitations­wechsel­wirkung zu umgehen. Man geht dazu über, die Masse eines Körpers nur durch seine Ruhe­masse darzu­stellen. Aller­dings wird dadurch der Effekt der dynamischen Masse ledig­lich in obige neue Impuls­definition verschoben. Das ändert aber grund­sätz­lich nichts an der klassischen Physik.

⇦ Kapitel Kapitel ⇨