Wie misst man denn eigentlich die Zeit? Eine Uhr, die sich für solche Gedankenexperimente sehr gut verwenden lässt, ist die sogenannte Licht-Uhr. Denn hier geht es nur um das Verhalten von Lichtwellen.
Bei der Licht-Uhr handelt es sich um eine Apparatur, bei der zwei Spiegel in einem Abstand zueinander angebracht sind. Zwischen beiden Spiegeln läuft ein Lichtsignal hin und her. Da die Spiegel eine gewisse Absorption aufweisen, verliert sich das Lichtsignal sehr schnell, sodass es nach jedem Durchlauf neu gestartet wird. Ein solcher Resonator ist ein periodischer Vorgang und gestaltet damit eine Uhr. Wenn die Spiegel beispielsweise einen Abstand von 15 cm haben, braucht das Licht für einen Durchlauf eine Nanosekunde (ns). Das ist dann quasi eine Nano-Uhr.
Jetzt könnte man eine solche Licht-Uhr in einem anderen Inertialsystem betrachten, welches sich mit gleichförmiger Geschwindigkeit vorbeibewegt. Wenn die Licht-Uhr an einem vorbeizieht, vollzieht der Lichtstrahl eine Zickzackbewegung. Und je schneller die Bewegung der Licht-Uhr ist, desto flacher ist dann der Einfallswinkel des Lichtes.
Wenn man hierbei an die Konstanz der Lichtgeschwindigkeit denkt, ist sowohl im Inertialsystem des Betrachters als auch im bewegten Inertialsystem die Geschwindigkeit des Lichts die gleiche. Aber im bewegten System ist der Weg wegen des Zickzackverlaufes länger. Das heißt, aus der Sicht desjenigen, an dem sich die Uhr vorbei bewegt, tickt die Uhr langsamer, weil der Weg des Lichtes länger ist. Und damit ist die Zeitmessung davon abhängig, wie sich die Uhren bewegen.
Wenn aus der Sicht eines Inertialsystems eine Uhr bewegt wird, wobei sie sich relativ zu diesem Inertialsystem bewegt, dann scheint die Periodendauer dieser bewegten Uhr verlängert. Die Zeit ist dabei nicht irgendetwas Undefiniertes, sondern eine Messgröße, die mit Uhren gemessen wird. Und wenn eine Uhr aus der Sicht eines bestimmten Bezugssystems eine längere Periodendauer hat, dann misst sie eine kürzere Zeit.
Warum verwendet man für die Zeitmessung zwei Uhren? Es geht darum, aus der Sicht des ruhenden Inertialsystems die Periodendauer einer bewegten Uhr zu bestimmen. Hierbei genügt es nicht, lediglich einen Wert abzulesen, denn dabei lässt sich nur die jeweilige Uhrzeit feststellen. Denn es sich nicht feststellen, wie schnell die Uhr „läuft”. Um die Ganggeschwindigkeit festzustellen, muss man zweimal draufschauen. Und um zweimal draufschauen zu können, muss man an zwei Stellen auf die relativ zu dem ruhenden System bewegte Uhr schauen.
Um das zu erreichen, überzieht man das ruhende Inertialsystem mit lauter synchronisierten Uhren, und vergleicht anschließend jeweils genau den Zeitpunkt, an dem bei der in Bewegung befindlichen Uhr der Lichtimpuls genau eine Periode durchlaufen hat. Diese Zickzackbewegung des Lichtsignals in der bewegten Uhr wird, mit der an der Periodenstelle befindlichen synchronisierten Uhr, im ruhenden System verglichen.
Das sind dann genau die beiden synchronisierten Uhren, bei denen aus Sicht der bewegten Uhr zunächst das Lichtsignal startet und nach einer Periode wieder eingefangen wird.
Grafik (wird später eingefügt)
Jetzt möchten wir den Verlauf des Lichtstrahls aus Sicht des ruhenden Inertialsystems in der bewegten Uhr betrachten und formal darstellen.
Wir gehen also davon aus, das ein Lichtstrahl von einer oben befindlichen Lichtquelle, von einem Punkt P, schräg hinunter verläuft. Anschließend trifft er auf den unteren Spiegel auf und wird schräg zurückreflektiert, wieder hinauf zum Punkt P. Die Uhr hat sich somit während einer Periode seitlich mit der Geschwindigkeit v fortbewegt. Längs dieses Weges breitet sich das Licht auf einem Zickzack-Weg mit der Geschwindigkeit c₀ aus. Je schneller die Uhr unterwegs ist, desto flacher wird die Zickzackbewegung und desto größer wird der Winkel φ.
Der Winkel φ lässt sich darstellen als:
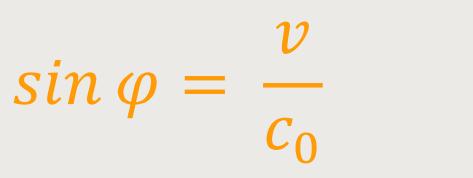
Im Allgemeinen wird der Winkel sehr klein sein, weil die Geschwindigkeit einer solchen Uhr im Verhältnis zur Lichtgeschwindigkeit auch sehr klein ist. Anders sieht es natürlich bei den Elementarteilchen aus, die man mit entsprechend hohen Energien, zum Beispiel im LHC, beschleunigt.
Wie schaut es jetzt mit den Periodendauern der Uhren aus, sowohl im ruhenden als auch im bewegten Inertialsystem? Je länger die Strecke des zurückgelegten Lichtsignals ist, desto länger ist auch deren Periodendauer.
Von Interesse ist insbesondere die Zeit Q am Punkt P, bis zu der Zeit Q', an dem der Lichtstrahl auf den ebenen Spiegel auftritt. Die Periodendauern der beiden Inertialsysteme sind jeweils proportional zu den Wegen, die das Licht zurücklegt.
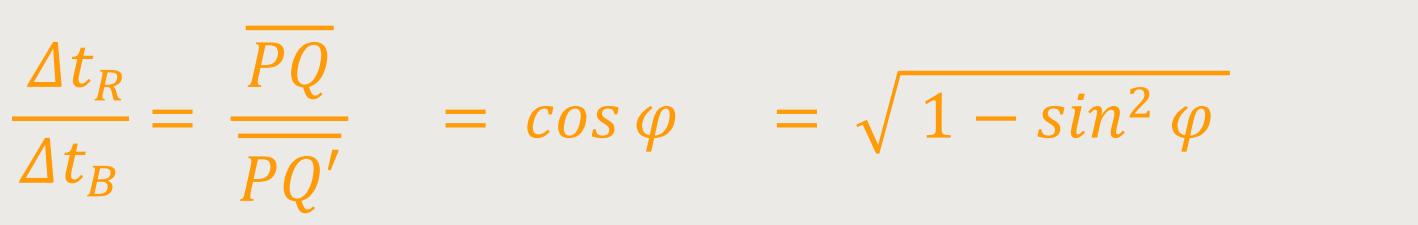
Sodass sich letztlich ergibt:
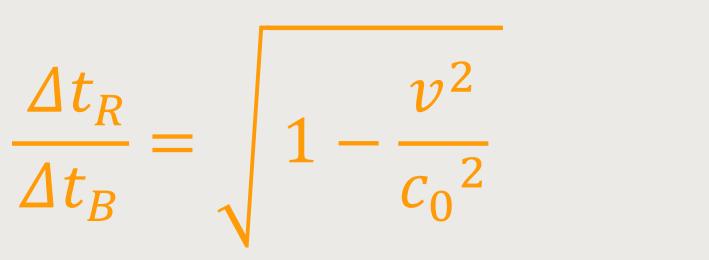
Wenn das Verhältnis der Periodendauern bekannt ist, stellt sich die Frage, wie man letztlich die Zeit abliest. Wenn die Periodendauer bei der Uhr um einen gewissen Faktor länger ist, wird die abgelesene Zeit um diesen Faktor kleiner ausfallen. Und was man tatsächlich an der bewegten und an der ruhenden Uhr abliest, ist der Reziprokwert.
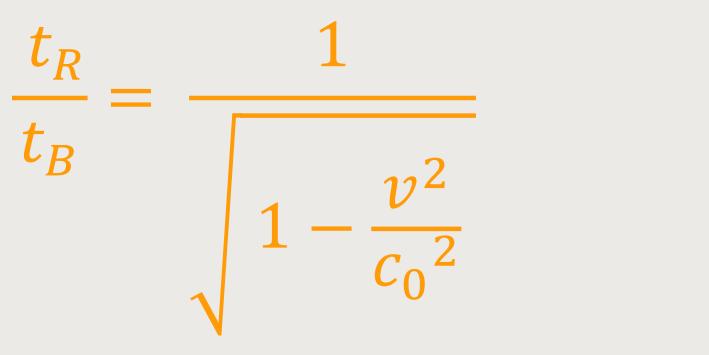
Damit lässt sich die Zeit an der bewegten Uhr definieren als:
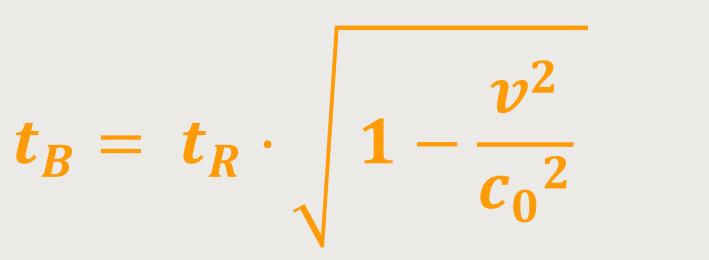
Man kann sofort erkennen, dass die Zeit, die mit der bewegten Uhr gemessen wird, kleiner ist als die Zeit, die mit den ruhenden Uhren gemessen wird. Daher müsste man eigentlich von einer „Zeitkontraktion” sprechen und nicht von einer Zeitdilatation. Der Begriff Dilatation bezieht sich deshalb auf die Periodendauer, die länger wird.
Grafik (Folie) (wird später eingefügt)
Der Begriff „Zeitdilatation” ist wie folgt definiert:
Für einen in einem Bezugssystem ruhenden Beobachter geht eine relativ
dazu bewegte Uhr langsamer − und misst somit eine geringere Zeit − als die in diesem
Bezugssystem ruhenden Uhren.
Wenn die Geschwindigkeit immer größer wird, und schließlich in die
Nähe der Lichtgeschwindigkeit kommt, geht der Faktor
Und damit entspricht der Wert c₀ einer Grenzgeschwindigkeit.
Grafik (Folie) (wird später eingefügt)
In dem Diagramm wird die Geschwindigkeit
Der k-Faktor ist definiert als:
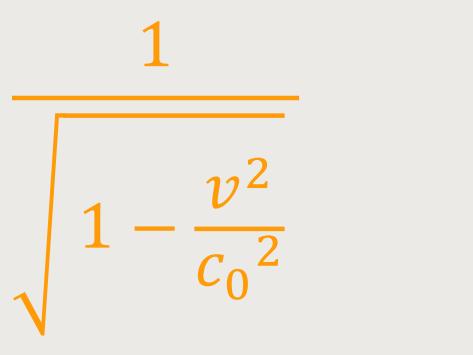
Ungefähr bei der Hälfte der Lichtgeschwindigkeit liegt die Gültigkeitsgrenze der klassischen Physik.
Grafik (Folie) (wird später eingefügt)
Grafik (Folie) (wird später eingefügt)
⇦ Kapitel Kapitel ⇨
