In der „Wellenoptik” befassen wir uns mit Aspekten, die durch die Lichtstrahlen und das Model der Strahlenoptik allein nicht beschrieben werden können. Das ist besonders dann der Fall, wenn man zu kleineren Objekten übergeht.
Mit einer Lochkamera kann man zwar die geradlinige Ausbreitung des Lichtes verfolgen. Wie ist es aber, wenn das Loch einer solchen Kamera um einiges kleiner ausfällt?
Wenn man zum Beispiel einen Laserstrahl durch ein kleines Loch mit gerade einmal
Die Ringe lassen sich nur durch einen Wellenaspekt des Lichtes erklären, sodass es zu Interferenz- und Beugungserscheinungen kommt. In diesem Kapitel werden wir primär die „Interferenzerscheinungen” betrachten.
Für derartige Betrachtungen verwendet man allerdings nicht Löcher sondern sehr häufig Spalte.
In einer solchen Versuchsanordnung schickt man den Laserstrahl durch einen sehr schmalen Einfachspalt. Und auch hier sieht man in der Mitte nicht nur eine helle Lichterscheinung, sondern seitlich verlaufend in beiden Richtungen „Interferenzerscheinungen”. Grund dafür ist offensichtlich eine wellenförmige Ausbreitung des Lichtes.
Jetzt stellt sich natürlich die Frage, warum solche Interferenzstreifen nicht ständig um uns herum in Erscheinung treten?
Die Beugungserscheinungen treten erst dann in Erscheinung, wenn die Objekte sehr klein sind, sprich wenn deren Größe in die Nähe der Lichtwellenlänge kommt. Zusätzlich ist entscheidend, dass sich verschiedene Wellen miteinander in bestimmter Weise überlagern.
„Interferenz” bedeutet, dass sich zwei Wellenzüge beispielsweise entweder in Phasengleichheit oder in einer Phasenverschiebung ausbreiten.
Grafik (wird später eingefügt)
Wenn sich Wellenzüge von zwei Quellen kommend phasengleich ausbreiten, spricht man von „konstruktiver Interferenz”. Der Gangunterschied ist jeweils ein Vielfaches der Wellenlänge.
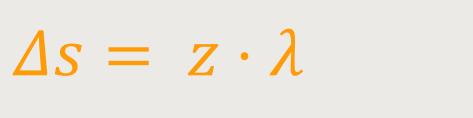
z ist ein ganze Zahl
λ ist die Wellenlänge
Wenn man dagegen die Situation betrachtet, bei der sich die Wellenzüge phasenverschoben ausbreiten, spricht man von einer „destruktiven Interferenz”.
Grafik (wird später eingefügt)

In diesem Fall werden sich die beiden Wellenzüge komplett auslöschen.
Dass sich Lichtwellen so ohne weiteres Überlagern können, liegt daran, dass die Wellengleichung eine lineare Differenzialgleichung ist. Derartige Gleichungen haben den Vorteil, dass lineare Kombinationen von Lösungen wieder Lösungen ergeben. Als Ergebnis kommt wieder ein physikalischer Wellenzug heraus.
Warum man Interferenzerscheinungen allerdings nicht überall beobachten kann, liegt daran, dass die Entstehung des Lichtes auf verschiedenen Vorgängen beruht. Das Licht wird nämlich in sogenannten „Wellenpaketen” ausgesandt.
Solche Wellenpakete werden deshalb ausgesendet, weil Licht immer dann emittiert wird, wenn ein Hüllenelektron von einem höheren Energiezustand in einen niedrigeren übergeht. In diesem Fall wird ein entsprechender Energiebetrag in Form eines Photons freigesetzt. Und ein solches Photon wird dann im Rahmen des Wellenmodels als ein solches Wellenpaket beschrieben.
Bei einem Schwall von derartigen Wellenpaketen kommt es aufgrund der sich ständig ändernden Anordnung andauernd zu Phasenverschiebungen. Deshalb lässt es sich im Alltag auch nicht beobachten. Wenn man solche Interferenzerscheinungen allerdings untersuchen möchte, muss sogenannte „Kohärenz” vorhanden sein. Das ist dann der Fall, wenn die Phasenbeziehung zwischen zwei Lichtwellen über eine genügend lange Zeit nahezu erhalten bleibt.
Die wichtigste Kohärenzgröße ist die
Daneben gibt es noch die
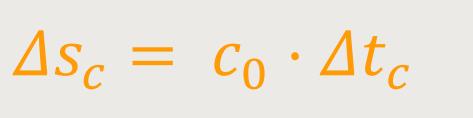
Beim Licht, welches beispielsweise von einer normalen Glühbirne ausgesendet wird, liegen die Kohärenzlängen in der Nähe von μm. Bei hochwertigen Lasern sind die Kohärenzlängen in der Gegend von km angesiedelt. Laser haben somit über lange Strecken konsistente Wellenzüge mit langgestreckten Wellenpaketen. Und erst durch diese technische Umsetzung lassen sich Beugungserscheinungen des Lichtes sichtbar machen.
Aber Licht in Form von elektromagnetischen Wellen durchsetzt den Raum in
Deshalb betrachtet man auch die Kohärenzfläche Fc. Darunter versteht man diejenige Querschnittsfläche, auf der keine nennenswerten Phasenunterschiede auftreten. Das bedeutet natürlich, dass die Phasenverschiebungen, die auf so einer Querschnittsfläche auftreten können, klein sind gegen die Lichtwellenlänge.
Wenn Licht durch so eine Querschnittsfläche hindurchtritt, wird sich auch ein Volumenbereich ergeben, innerhalb dessen eine genügende Kohärenz der Wellenzüge vorhanden ist. Ein solches Volumen bezeichnet man als das Kohärenzvolumen ΔVc. Somit wird das Kohärenzvolumen definiert als:
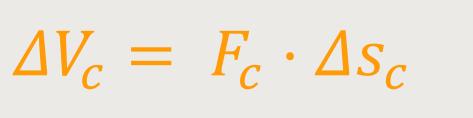
Der erste, dem das gelungen ist, Interferenz zu beobachten, war Thomas Young (1802). Er betrachtete von einem Lichtwellenzug nur einen sehr kleinen Querschnitt. Young verwendete für seinen Versuch Sonnenlicht, also inkohärentes Licht. Er beschreibt seinen Versuchsaufbau wie folgt:
"Ich machte ein kleines Loch in einen Fensterladen, überdeckte es mit einem Stück dicken Papieres, in das ich mit einer feinen Nadel ein Loch stach, und benutze einen Spiegel, um den dünnen Lichtstrahl umzuleiten, der durch das Loch kam. Ich nahm die dünne, ungefähr ein dreißigstel Inch (ca. 0,85 mm) breite Seite einer Spielkarte und hielt sie in den Weg des Lichtstrahls, sodass dieser zweigeteilt wurde. Ich beobachtete den Schatten: neben farbigen Streifen zu beiden Seiten des Schattens war der Schatten selbst durch ähnliche parallele Streifen geteilt."
Quelle: T. Young 1804 Experiments and calculations relative to physical optics (The 1803 Bakerian Lecture) Philosophical Transactions of the Royal Society of London 94 1-16Grafik (wird später eingefügt)
Wenn zwei Spalte nahe genug beieinander liegen, entstehen quasi zwei nebeneinander befindliche Lichtquellen. Der Lichtwellenzug wird beim Auftreffen auf die Spalte, aufgrund des kleinen Spaltabstandes, anschließend kohärente Lichtquellen darstellen. Hinter dem Doppelspalt wird sich das Licht dann in Form von Kugelwellen ausbreiten. Und aufgrund der Kohärenz lassen sich schließlich Überlagerungen deutlich erkennen.
Grafik (Folie) (wird später eingefügt)
Der „Doppelspalt” ist in der Physik von größter Bedeutung. Auch zum besseren Verständnis quantenmechanischer Phänomene dient der Spalt als Grundlage, denn auch bei anderen Strahlen von Teilchen (Elektronen, Protonen, Neutronen) zeigen sich ebenfalls Interferenzerscheinungen.
Nach heutiger Sicht: Wenn man einen Detektor an beiden Spalten positioniert, um festzustellen durch welchen Spalt das Elektron hindurchtritt, verschwinden die Interferenzerscheinungen. Wenn man dagegen keinen Detektor hinstellt, bleiben die Interferenzerscheinungen erhalten.
Die Quantenmechanik ist insofern ein Gebiet, bei dem der Aspekt der Informationsübertragung eine äußerst große Rolle spielt. Die Wellenoptik zeigt Interferenzerscheinungen, die mit klassischen Methoden nicht verstanden werden können.
Einen weiteren Versuch hatte Augustin J. Fresnel (1821) unternommen. Er konnte mit Hilfe eines Winkelspiegels zwei kohärente Lichtquellen noch konkreter darstellen.
Grafik (Folie) (wird später eingefügt)
Einer, der sich auf dem Gebiet der Optik besonders verdient gemacht hat, war der Physiker Albert A. Michelson. Er hatte ein „Interferometer” erfunden, mit dessen Hilfe man die Interferenzen messen konnte.
Grafik (Folie) (wird später eingefügt)
Mit einem solchen Interferometer lässt sich das Maximum und das Minimum einer Interferenz ermitteln und damit auch die Kohärenzlänge gut sichtbar machen. Wenn man in einen der beiden Lichtwellenzüge zum Beispiel zusätzlich noch ein Dielektrikum einfügt, lassen sich Präzisionsmessungen des Brechungsindexes dieses Mediums durchführen. Darüber hinaus kann auch die Lichtwellenlänge quantitativ bestimmt werden.
Michelson war der erste, der den Brechungsindex von Luft aufgrund der Änderung des entsprechenden Interferenzmusters ermittelte. Man spricht in diesem Zusammenhang auch von einer „Zweistrahl-Interferenz”.
Später hat sich gezeigt, dass die Interferenzen noch wesentlich deutlicher sichtbar werden, wenn nicht nur zwei Strahlen miteinander in Interferenz gebracht werden, sondern viele Strahlen, die jeweils eine gewisse Phasenbeziehung zueinander haben. Dann kommt es zu einer deutlichen Aufschärfung der Interferenz.
Grafik (Folie) (wird später eingefügt)
Bei sehr vielen Strahlungsquellen bilden sich die Interferenzen zu scharfen Resonanzspitzen aus. Durch ein solches Verfahren wird die Messmethodik um ein Vielfaches genauer. Das erreicht man insbesondere durch ein Fabry-Perot-Interferometer.
Grafik (Folie) (wird später eingefügt)
Hierbei wird von einer ausgedehnten Lichtquelle die ausgehenden Strahlen durch eine Sammellinse zu einem parallelen Strahlenbündel umgewandelt. Anschließend trifft das Bündel unter einem bestimmten Winkel auf ein Glasplatten-Paar. Jedes Glas hat eine bestimmte Brechung und Reflexion. Der entsprechende Winkel ϑ ist entscheidend dafür, dass einige reflektierte Strahlen mit dem parallel verlaufenden Strahlenbündel zusammentreffen und sich überlagern.
Dadurch kommt es zu einer „Vielstrahl-Interferenz”. Je nachdem welcher Winkel und welcher Abstand zwischen den Glasplatten gewählt wird, kommt es zu konstruktiver oder destruktiver Interferenz. Abschließend wird das Parallelstrahlenbündel in einer zweiten Sammellinse gebündelt, und auf einem Beobachtungsschirm ein Ringmuster abgebildet.
Grafik (Folie) (wird später eingefügt)
Wenn man unter einem bestimmt Winkel ϑ auf die Glasflächen einstrahlt, kommt es zu einer gewissen Phasendifferenz und Wegdifferenz, die sich definieren lässt als:

Grafik (Folie) (wird später eingefügt)
Haben solche Glasplatten eine relativ schlechte Reflexivität, wird der Lichtstrahl nicht sehr oft reflektiert. Dann kommt es nur zu einer Sinuskurve in Abhängigkeit von dem Winkel ϑ. Wenn dagegen eine oder beide Glasplatten im Innern etwas mehr verspiegelt werden, beginnen die Einbrüche der Lichtstrahlen immer größer zu werden, und damit werden die Maxima immer schärfer. Bei einem Wert von 0,95 kommt es zu ganz scharfen Abgrenzungen mit dazwischen liegenden Dunkelbereichen. Mit solch scharfen Resonanzmaxima lassen sich Wellenlängen und Distanzen mit sehr großer Genauigkeit ermitteln.
⇦ Kapitel Kapitel ⇨
