Nun stellt sich die Frage, wie es im Einzelnen mit den Koordinaten­systemen aussieht, wenn die Lorentz-Trans­formation als Grund­lage dient.

Zunächst nochmals eine kurze Gegenüber­stellung beider Trans­formationen:

Gemäß Galilei-Trans­formation:

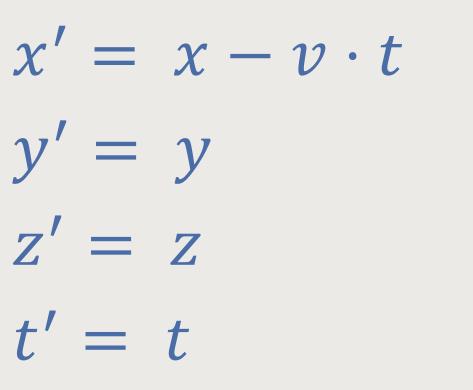
Gemäß Lorentz-Trans­formation:

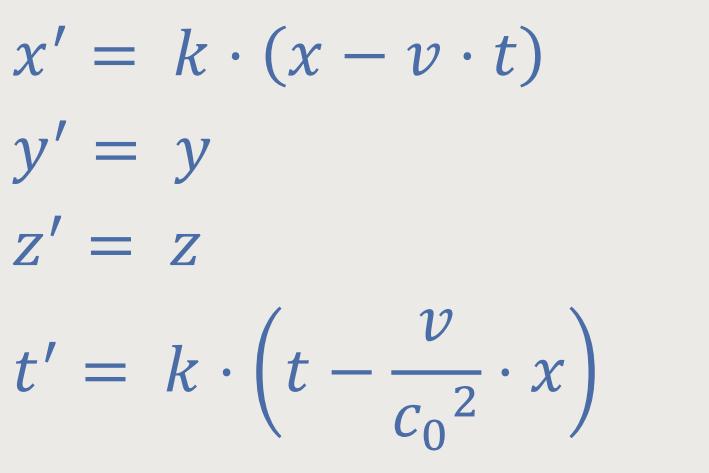
Durch eine nähere Betrachtung wird sich zeigen, worin die wesent­lichen Unter­schiede zwischen der Sicht­weise der klassischen Mechanik und der Relativitäts­mechanik liegen.

Die Diagramme, basierend auf der Galilei-Trans­formation, sind nur räum­liche Diagramme. In der klassischen Mechanik spielt die Zeit eher eine unter­geordnete Rolle. Entspre­chend unseres Vorstellungs­vermögens bewegen wir uns über­wiegend in 3-dimensionalen Systemen.

Aber aufgrund der Lorentz-Trans­formation lässt sich erkennen, dass die Zeit­koordinate mit einbe­zogen werden muss, weil sich die Zeit beim Trans­formieren auch ändert. Deswegen muss die Zeit in den grafischen Darstel­lungen mit berück­sichtigt werden. Und dem­entspre­chend bewegt man sich in einem 4-dimensionalen Raum.

Weil sich aber ein 4-dimensionaler Raum nicht leicht verständ­lich darstellen lässt, greift man hierzu einen Aus­schnitt aus einem solchen Raum heraus, indem man sich auf 2 von 4 Dimen­sionen konzen­triert. Daraus lässt sich dann ein x-t-Diagramm abbilden.

Grafik (wird später eingefügt)

Da es ja um die Unter­schiede in der Sicht­weise beider Trans­formationen geht, bildet zunächst wieder die Galilei-Trans­formation die Ausgangs­situation.

Die x-Achse wird in Metern [m] ange­geben, und die t-Achse in Sekunden [s]. Wenn sich jetzt ein Körper bewegt, lässt sich das durch einen Linien­zug im Diagramm darstellen. Damit weiß man zu jedem Zeit­punkt, wo sich der Körper befindet. Eine solche Linie wird auch als „Welt­linie” bezeichnet.

Darüber hinaus wird die t-Achse eben­falls als „Welt­linie” bezeichnet. In diesem Fall ent­spricht diese Achse bei x = 0 der Welt­linie des Koordinaten­ursprungs. Und die x-Achse stellt alle Ereig­nisse dar, die zu irgen­deinem Zeit­punkt, in diesem Fall t = 0, gleich­zeitig statt­finden.

Jetzt wollen wir das Ganze auf ein bewegtes Bezugs­system trans­formieren. Und hier bewegt sich insbe­sondere der Ursprung des Systems I' relativ zum System I.

Die t'-Achse ist die Achse, an der x' = 0 ent­spricht. Und wenn das der Fall ist, dann gilt:

Oder anders ausge­drückt:

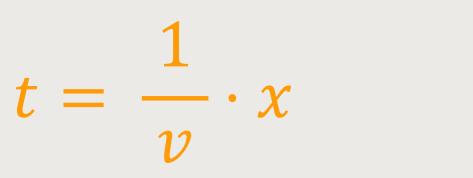
Analog dazu ent­spricht die x'-Achse der Achse, an der t' = 0 ist.

Grafik (wird später eingefügt)

Hierzu kann in einem x-t-Diagramm das bewegte System, beste­hend aus x'-Achse und der t'-Achse der mit einer Relativ­geschwindig­keit von v = 0,5 m/s einge­tragen werden. Dann liegen beide Koordinaten­systeme im gleichen Ursprung über­einander, wobei die t'-Achse nicht mehr senkrecht auf der x'-Achse steht, sondern im Diagramm gekippt darge­stellt wird, entspre­chend der Relativ­geschwindig­keit. Denn bei dem bewegten Bezugs­system bewegt sich der Ursprung relativ zu dem unbewegten x-t-System. Inso­fern ent­spricht t' der Weltlinie des bewegten Koordinaten­ursprungs im System I'.

Wenn also eine Trans­formation auf ein bewegtes Bezugs­system durch­führt wird, kippt die Zeit-Achse. Die Welt­linie stellt die Menge aller Punkte dar, an denen sich ein bewegter Körper auf­hält. Es handelt sich dabei immer um Parallel-Koordinaten­systeme. Die x'-Achse wird aller­dings nicht kippen, weil für beide Systeme t' = t gilt.

Jetzt werden wir nochmals die gleichen Über­legungen aus relativis­tischer Sicht­weise betrachten. Da man es hier mit wesent­lich größeren Geschwindig­keiten zu tun hat, muss man die Achsen entspre­chend anders skalieren.

Grafik (wird später eingefügt)

Die x-Achse wird jetzt in Metern [10⁸ m] ange­geben, und die t-Achse wieder in Sekunden [s]. Nun soll entspre­chend der Skalie­rung die Welt­linie ein sich ausbrei­tendes Licht­signal dar­stellen.

Da die t-Achse wieder eine Welt­linie ist, ent­spricht diese Achse bei x = 0 der Welt­linie des Koordinaten­ursprungs. Und die x-Achse stellt auch hier alle Ereig­nisse dar, die zu einem Zeit­punkt, in diesem Fall t = 0, gleich­zeitig statt­finden.

Erneut wird das Ganze auf ein bewegtes Bezugs­system trans­formiert. Nach wie vor bewegt sich der Ursprung des Systems I' relativ zum System I.

Auch hier gilt für die t'-Achse x' = 0. Und wenn das der Fall ist, gilt analog zu oben:

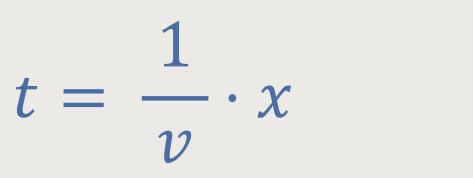
Ähnlich ent­spricht die x'-Achse eben­falls der Achse, an der t' = 0 ist. Aller­dings gibt es jetzt einen wesent­lichen Unter­schied, denn bei der Lorentz-Trans­formation gilt jetzt:

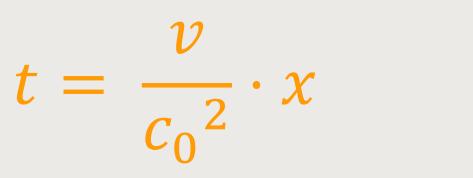
Nun wird erneut das bewegte System, diesmal mit einer Relativ­geschwindig­keit von v = 10⁸ m/s, in das Diagramm einge­tragen, wobei die x'-Achse in 3-er Schritten skaliert ist. Wie nicht anders zu erwarten, kippt auch hier die Zeit-Achse. Auf­grund der gewähl­ten Skalie­rung kippt die x'-Achse ähn­lich wie bei der Galilei-Trans­formation.

Bisher gab es keine Unter­schiede zwischen beiden Trans­formationen. Doch nun macht sich ein Unter­schied bei der x'-Achse bemerk­bar. Denn bei hohen Geschwindig­keiten nahe der Licht­geschwindig­keit kippt eben­falls die x-Achse und wird zu einer x'-Achse.

Grafik (wird später eingefügt)

Wenn man in einem Parallel­koordinaten­system mit senk­recht auf­einander liegenden Achsen ein Ereignis E und gleich­zeitig ein Ereignis mit einer höheren Geschwindig­keit betrachtet, finden beide Ereig­nisse im System I beispiels­weise zum Zeit­punkt t = 0 statt. Aber auf­grund der gekippten x'-Achse finden jetzt diese beiden Ereig­nisse im System I' nicht mehr gleich­zeitig statt.

Somit lässt sich wieder fest­stellen, dass die Gleich­zeitig­keit nur auf ein bestimmtes Inertial­system bezogen ist. Bei unter­schied­lichen Inertial­systemen sind dieselben Ereig­nisse an verschie­denen Orten nicht mehr gleich­zeitig.

Grafik (wird später eingefügt)

Wenn man jetzt noch zusätz­lich das Licht­signal in beide über­lagerten Diagramme einträgt, breitet sich dieses Signal sowohl im x-t-Diagramm als auch im x'-t'-Diagramm mit Licht­geschwindig­keit aus. Die Welt­linie dieses Licht­signals liegt jetzt symmetrisch zu den Achsen der beiden über­lagerten Diagramme.

Das hinauf­kippen der x-Achse hat einer­seits zur Folge, dass sich die Gleich­zeitig­keit nur noch auf ein bestimmtes Bezugs­system bezieht, und dass sich ander­seits das Licht­signal in Bezug auf das Bezugs­system mit den gekippten Achsen, also dem System I', wieder mit Licht­geschwindig­keit aus­breitet. Damit wird deut­lich, dass Raum und Zeit ähn­liche struktu­relle Eigen­schaften haben.

Grafik (wird später eingefügt)

In Erweite­rung dessen lässt sich ledig­lich ein x-y-t-Diagramm dar­stellen, das zumin­dest aus 3 Dimensionen besteht. In einem solchen Diagramm lässt sich solch ein Licht­signal in Form eines Kegels auf­tragen. Das ent­spricht einem sich ausbrei­tenden Kreis, bei dem sich das Licht mit fort­schrei­tender Zeit ausbreitet.

Bei einem solchen Kegel liegen alle zukünf­tigen Ereig­nisse ober­halb der Bezugs­ebene und inner­halb des Licht­kegels, wogegen alle Ereig­nisse aus der Vergangen­heit unter­halb der Bezugs­ebene und inner­halb des unteren Licht­kegels liegen. Aber alle Ereig­nisse außer­halb der sich kreuzenden Lichtkegel oder die direkt auf der Bezugs­ebene liegen, repräsen­tieren Ereig­nisse der Gegenwart.

Anhand der Lorentz-Trans­formation werden wir abschlie­ßend noch betrachten, wie sich die Addition von Geschwindig­keiten darstellt.

Dazu denkt man sich wieder einen Zug, der beispiels­weise gerade durch einen Bahn­hof fährt. Ein Beobachter betrachtet aus Sicht des Gleis­körpers dieses Ereignis und sieht, wie im Zug gerade ein Schaffner von einem Abteil ins nächste geht.

Nun stellt sich die Frage, wie schnell bewegt sich der Schaffner relativ zum Gleis­körper?

Spontan würde man denken, man benötigt die Summe aus der Zug­geschwindig­keit relativ zum Gleis­körper, zuzüg­lich der Geschwindig­keit des Schaffners relativ zum Zug. Stimmt das aber wirklich? Gehen wir einmal der Frage auf den Grund.

Für das System des Gleis­körpers gelten die Kompo­nenten x, y, z, t.

Und für das System des Zuges gelten die Kompo­nenten x', y', z', t'.

Der Zug bewegt sich mit der Geschwindig­keit u relativ zum Gleis­körper. Und der Schaffner bewegt sich mit Geschwindig­keit v relativ zum Zug. Dann wäre die Bewegung des Schaffners relativ zum Gleis­körper vermeint­lich u + v.

Jetzt rechnen wir obiges Beispiel relativis­tisch aus Sicht der Lorentz-Trans­formation durch hier mit (v, w):

Für die Geschwindig­keit v des Schaffners relativ zum Zug gilt:

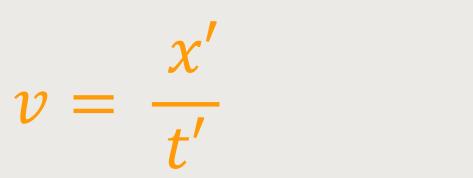
Für die Geschwindig­keit w des Schaffners relativ zum Gleis­körpers gilt:

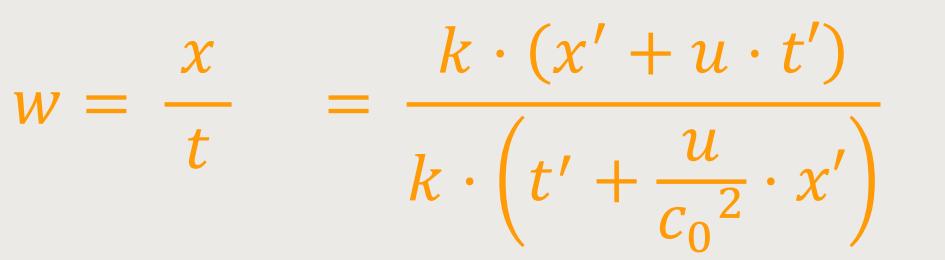
Wenn man jetzt Zähler und Nenner durch t' dividiert, ergibt sich:

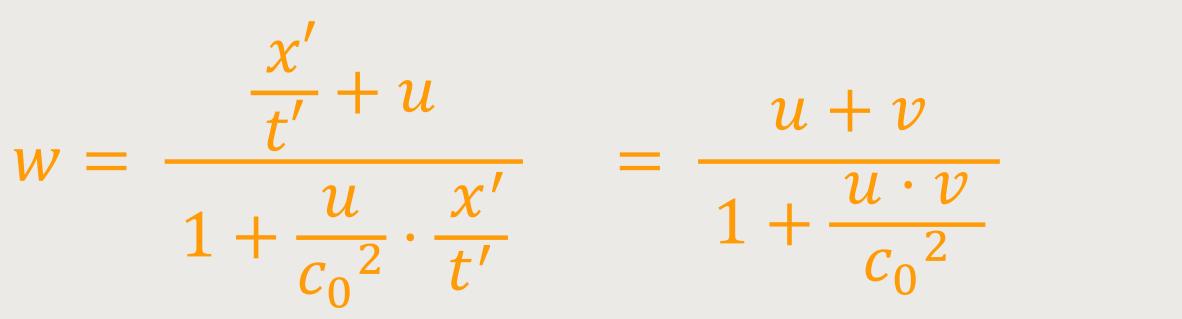
Wie man erkennen kann, kommt etwas anderes heraus. Das Ergebnis ent­spricht nicht u + v, wie man zunächst viel­leicht erwarten würde.

Wenn der Zug sehr lang­sam ist, und der Schaffner im Verhält­nis dazu erst recht, dann fällt der Nenner quasi weg. Und das ent­spräche tatsäch­lich der Anfangs­über­legung. Aber wenn man sich im Bereich der Licht­geschwindig­keit bewegt, trifft das nicht mehr zu.

Hierzu ein Rechen­beispiel:

Das Beispiel hinkt natür­lich, weil jetzt Zug und Schaffner jeweils mit Licht­geschwindig­keit unter­wegs sind. Aber was wäre wenn? Dann würde sich folgendes ergeben:

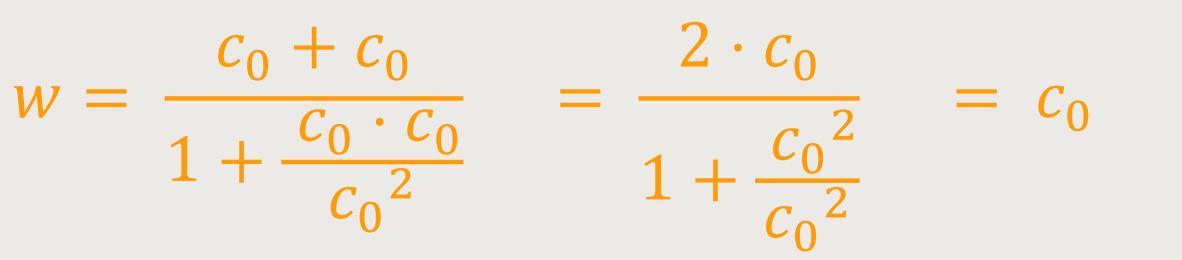
Hier bestätigt sich, dass der Schaffner dem Licht nicht voraus­eilen kann. Schneller als das Licht bewegt sich nichts, und damit ent­spricht c_₀ nach wie vor der Grenz­geschwindig­keit.

Es scheint also so zu sein, dass ein Körper bei zuneh­mender Geschwindig­keit immer träger wird und sich nicht weiter beschleu­nigen lassen will. Was der Grund dafür sein könnte, betrachten wir im näch­sten Kapitel.

⇦ Kapitel Kapitel ⇨