Jetzt geht es darum, sich klar zu machen, was es mit dem Trans­formieren zwischen verschie­denen Bezugs­systemen auf sich hat, und wir wollen versuchen unsere Erfah­rungen hinsicht­lich Längen­kontraktion und Zeit­dilatation sowie dem Fehlen der abso­luten Gleich­zeitig­keit in ein gemeinsames Konzept zu bringen. Das alles gelingt mithilfe der „Lorentz-Transf­ormation”.

In diesem Zusammen­hang betrachten wir im Nach­folgenden zwei Inertial­systeme I und I'. Beide Systeme sollen sich relativ zuein­ander mit einer Geschwindig­keit v bewegen. Des Weiteren werden wir dabei die Orts- und Zeit­koordinaten betrachten. Die Orts­koordinaten nennen wir x, y, z und die Zeit­koordinaten t.

Außerdem setzten wird voraus, dass die räum­lichen Koordinaten senk­recht auf­einander liegen. Und die Koordinaten­achsen beider Systeme sind alle parallel zuein­ander. Zur der Zeit t = t' = 0 fallen die Ursprünge O = O' zusammen. Die Relativ­bewegung dieser beiden Systeme zuein­ander sei in Richtung der x-Achse.

Zuvor werden wir das Ganze aus Sicht der Galilei-Trans­formation betrachten.

Grafik (wird später eingefügt)

Wenn eine gewisse Zeit t verstrichen ist, wird sich der Ursprung von dem System I' um die Strecke v · t weiter­bewegt haben. Und wenn man irgendein Ereignis E betrachtet, das zugleich in beiden System darge­stellt wird, dann geben die Koordinaten x, y dieses Ereignis im System I an, und die Koordinaten x', y' desselben Ereig­nisses im System I'. In diesem Fall gilt:

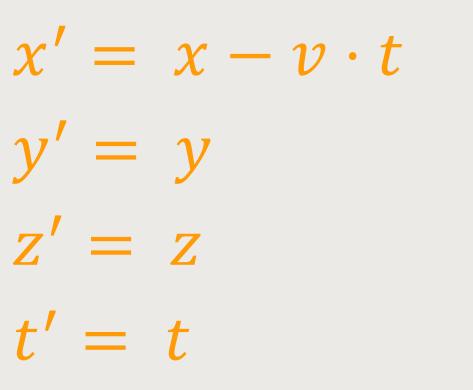
Das lässt sich sofort umformen:

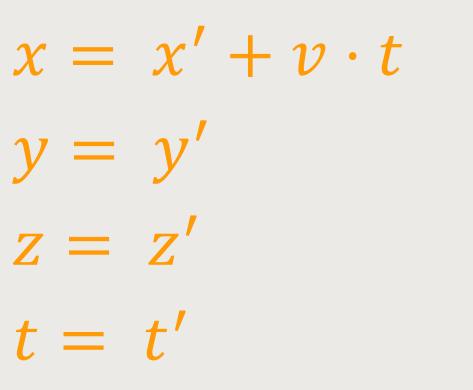
Das ist die klassische Bewegung bei der Galilei-Trans­formation.

Aus dieser Gegen­über­stellung sieht man, dass es egal ist, ob man einer­seits das System I' relativ zum System I mit der Geschwindig­keit v bewegen lässt, oder das System I relativ zum System I' mit der Geschwindig­keit −v. Und das ist dann ein Zeichen dafür, dass die Galilei-Trans­formation das Relativitäts­prinzip erfüllt (siehe vorheriges Kapitel). Es muss sich jeweils aus Sicht des einen Systems, das andere System mit der Geschwindig­keit v bewegen, entweder in die eine oder in die andere Richtung, je nach Sicht­weise.

Aber es stellt sich auch die Frage, ob das Prinzip von der Konstanz der Licht­geschwindig­keit eben­falls durch diese Trans­formation wieder­gegeben wird?

Hierzu kann man ein Licht­signal betrachten, das sich längs der x-Achse in dem System I ausbreitet. In diesem Fall gilt:

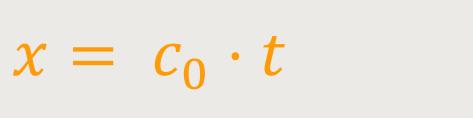
Wenn man diese Beziehung auf das System I' trans­formiert, erhält man zunächst:

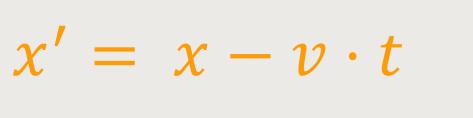
Durch Einsetzten ergibt sich:

Man sieht sofort, dass sich das Licht­signal im System I' keineswegs mit Licht­geschwindig­keit ausbreitet, sondern mit (c₀ − v) · t'. Das wider­spricht der Konstanz der Licht­geschwindig­keit. Daher führt hier die Galilei-Transformation nicht ans Ziel, und es ist not­wendig einen anderen Weg zu beschreiten.

Deshalb gehen wir jetzt zu einer anderen Trans­formation über, und zwar der bereits ange­sprochenen Lorentz-Transformation. Bezogen auf die Koordinaten in dem System I und I' erhalten wir ähn­liche Werte. Aller­dings wird nun noch ein Korrektur­faktor k einge­führt, und es kommt bei der Zeit noch ein zusätz­licher Term hinzu.

Grafik (Folie) (wird später eingefügt)

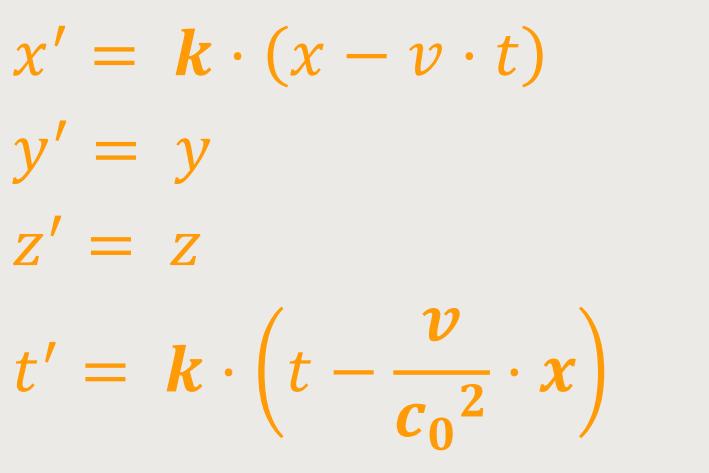
k   ist ein Korrektur­faktor (siehe Zeit­dilatation)

Das lässt sich ebenfalls sofort umformen:

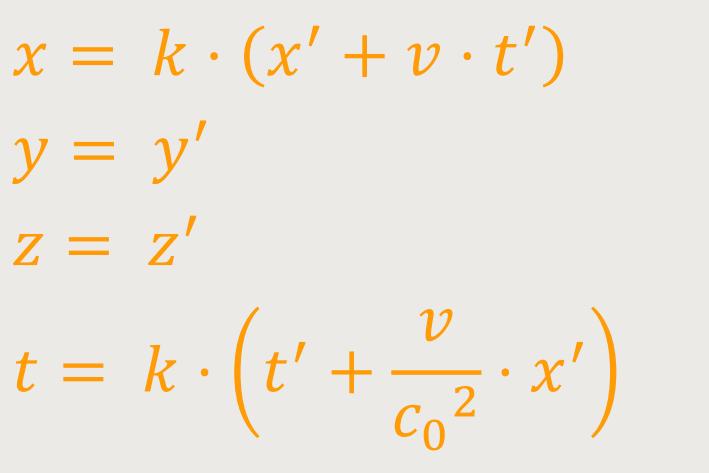
An dieser Stelle sei erwähnt, wenn die Geschwindig­keit v sehr klein ist im Verhält­nis zur Licht­geschwindig­keit, wird der k-Faktor zu 1 und führt unmittel­bar zurück zur Galilei-Trans­formation.

Aber grund­sätzlich erfüllt die Lorentz-Trans­formation das Relativitäts­prinzip. Und wie sieht es hier mit der Konstanz der Licht­geschwindig­keit aus?

Auch hier gehen wir zunächst davon aus, dass es ein Licht­signal entlang der x-Achse im System I gibt. In diesem Fall gilt gleich­falls:

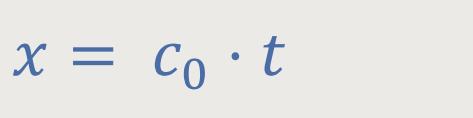
Wenn man diese Beziehung erneut auf das System I' trans­formiert, erhält man das Verhält­nis der Bewegung auf der x-Achse zur verstri­chenen Zeit:

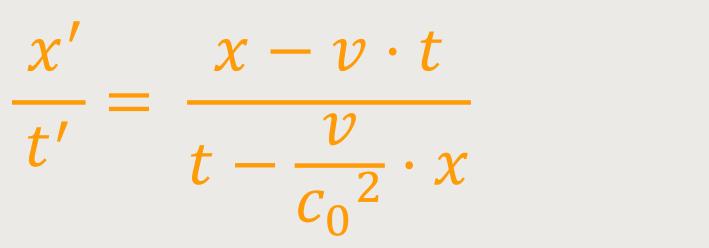
Durch Einsetzten erhält man:

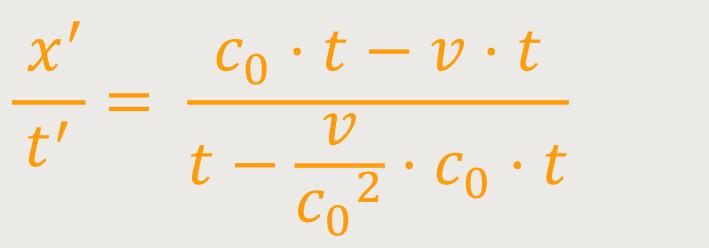
Nach Umformung ergibt sich:

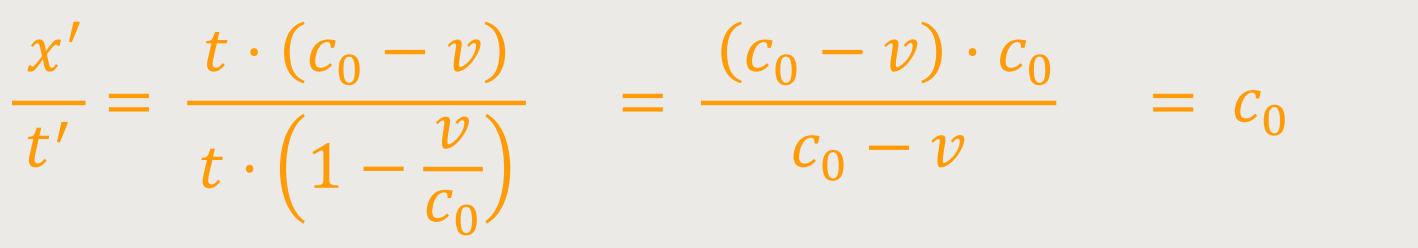
Und damit haben wir das Prinzip von der Konstanz der Licht­geschwindig­keit bestätigt. Das ist der über­zeugende Vorteil der Lorentz-Trans­formation gegen­über der Galilei-Trans­formation.

Alles in allem handelt es sich um eine Koordinaten-Trans­formation zwischen zwei Systemen, so dass beide Grund­prinzipien der Speziellen Relativitäts­mechanik, nämlich das Prinzip von der Relativi­tät und auch das Prinzip von der Konstanz der Licht­geschwindig­keit erfüllt sind.

Diese Koordinaten-Trans­formation bildet die Grund­lage für die weitere Betrach­tung. Dabei gilt zu berück­sichtigen, dass die Zeit bei den relativis­tischen Über­legungen eben­falls eine wesent­liche Rolle spielt, und diesem Umstand wird eben­falls Rechnung getragen.

Deshalb werden wir uns als nächstes verschie­dene x-t-Diagramme anschauen.

⇦ Kapitel Kapitel ⇨