Aus dem was man über die Zeit­messung erfahren kann, lässt sich auch viel über die „Längen­messung” erfahren.

Grafik (Folie) (wird später eingefüügt)

Hierzu kann man gedank­lich ein ganz ähn­liches Experiment noch einmal durch­führen, wie das vorherige mit der Zeit­dilatation. Wir haben im unteren Bereich wieder zwei ruhende Uhren und ober­halb aber­mals eine bewegte Uhr. Genau zwischen den beiden ruhenden Uhren verharrt ein läng­licher Stab in Ruhe, dessen Länge dem Abstand der Uhren ent­spricht. Inso­fern lässt sich die Länge des Stabes eben­falls messen. Aus Sicht der bewegten Uhr saust nun der Stab vorbei.

Wie schaut es jetzt mit der Messung der Länge aus? Man könnte die Über­legung anstellen, die Länge nicht mit einem Maßstab zu messen, sondern sich an der Zeit zu orien­tieren die verstreicht. Das heißt, die Zeit die verstreicht, wenn die bewegte Uhr einmal bei der ersten ruhenden Uhr, also dem Anfangs­punkt des Stabes vorbei­saust, und einmal bei der zweiten ruhenden Uhr, sprich dem End­punkt des Stabes. Das Ergebnis der Messung wird genauso aus­fallen, wie zuvor bei den drei Licht­uhren.

Aus Sicht des ruhenden Beobachters ist die Länge dieses Stabes identisch mit der Geschwindig­keit der vorbei­fliegenden Uhr multi­pliziert mit der Zeit die verstrichen ist. Wenn man jetzt dagegen die Situation aus Sicht der bewegten Uhr betrachtet, bewegt man sich zunächst einmal mit der Uhr. Und damit ruht für den Mitfliegenden die Uhr, während der läng­liche Stab an einem vorbei saust. Will man aber die Länge des bewegten Objektes fest­stellen, muss man den konkreten Zeit­punkt fest­halten, wann man am Anfang und am Ende des Stabes vorbei­fliegt. Auch hier wird die Uhr im bewegten System aufgrund der Zeit­dilatation eine kürzere Zeit anzeigen.

Aufgrund des Relativitäts­prinzips hat die bewegte Uhr aus Sicht des ruhenden Beobachters die Geschwindig­keit v. Und umgekehrt hat auch aus Sicht der bewegten Uhr der Stab betrags­mäßig die Geschwindig­keit v. Die Relativ­geschwindig­keit ist aus beiden Sicht­weisen die gleiche. Trotzdem sind die Geschwindig­keiten im jeweils betrachteten Inertial­system unter­schiedlich. Die kürzere Zeit­messung im bewegten System ist nicht nur schein­bar so, sondern sie wird tatsäch­lich gemessen. Und das bezeichnet man über­tragen auf die Längen­messung als die „Längen­kontraktion”.

Wie beim vorhe­rigen Experiment mit den Licht­uhren, muss gleicher­maßen auch die gemessene Länge bei einem solchen Stab geringer ausfallen, wenn man der Länge nach an dem Stab vorbei­saust.

Wird die Zeit­messung als Grund­lage für die Längen­messung heran­gezogen, wird die Länge je nach Inertial­system unter­schiedlich ausfallen. Die Differenz ent­spricht dem gleichen Faktor wir bei den Licht­uhren.

Und damit lässt sich die Länge an der bewegten Uhr definieren als:

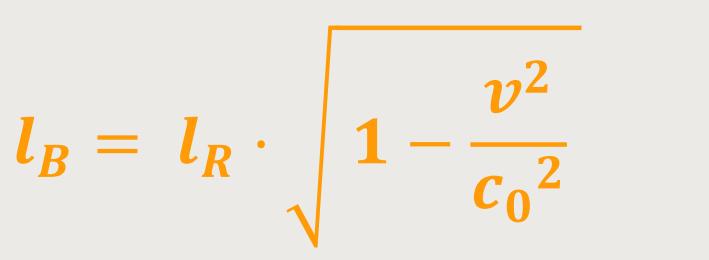
Grafik (Folie) (wird später eingefügt)

Bei der Längen­kontraktion verhält es sich so, dass wenn die Geschwindig­keit des Stabes aus Sicht des bewegten Inertial­systems immer größer wird und schließlich in die Nähe der Licht­geschwindig­keit kommt, die gemessene Länge des bewegten Körpers immer kleiner wird und schließ­lich gegen Null geht. Das heißt, die bewegte Uhr bleibt auch hier stehen bzw. sie zeigt nichts mehr an und man misst letzt­lich auch keine Länge.

Und damit entspricht auch hier der Wert c_₀ der Grenz­geschwindig­keit.

Natür­lich misst man im Alltag die Längen von Körpern nicht mittels Licht­uhren, sondern mit Maßstäben. Als Ergebnis erhält man immer die Ruhelänge. Das Problem tritt erst ein, wenn sich der Stab bewegt, vor allem wenn er sich viel­leicht mit halber Licht­geschwindig­keit fort­bewegt. Und dann ist es nicht mehr möglich gleich­zeitig abzu­lesen. Denn Gleich­zeitig­keit ist in beiden Inertial­systemen jeweils etwas anderes. In unter­schied­lichen Bezugs­systemen ist die Länge des Stabes tatsächlich unter­schiedlich, weil sie unter­schied­lich gemessen wird.

Zum Thema „Längen­kontraktion” kann man zum besseren Verständnis einige Beispiele betrachten.

Grafik (wird später eingefügt)

Im ersten Beispiel geht es um eine foto­sensitive Platte, über die sich ein läng­licher Gegen­stand mit einer Geschwindig­keit v bewegt. Ober­halb sind einige Blitz­lampen ange­bracht. Sobald dieser läng­liche Körper die Mitte der Platte erreicht hat, werden die Blitz­lampen ausge­löst und die Foto­platte wird belichtet. Anschlie­ßend kann man die Länge messen und hält den Wert für die Ruhe­länge des Körpers.

Nun stellt sich die Frage, ist das tatsäch­lich die „Ruhe­länge” oder die Länge, die man auf­grund der Längen­kontraktion erwarten würde. Entschei­dend ist hierbei, wann leuchtet welche Blitz­lampe auf. Es ist, wie so oft, eine Sache der nicht universellen Gleich­zeitig­keit. In dem ruhenden System, in welchem sich die Foto­platte und die Blitz­lampen befinden, herrscht eine Gleich­zeitig­keit. Wenn man sich dagegen wieder auf den Stand­punkt des vorbei­fliegen­den Körpers begibt, und von dort beobachtet was passiert, blitzen die Lampen nicht gleich­zeitig auf.

Hendrik A. Lorentz hat 9 Jahre nach Michelson im Jahre 1895 eine Trans­formation aufge­stellt, mit der er den Fehl­schlag des Michelson-Experiments erklären wollte. Er hat nämlich so trans­formiert, dass der eine Arm des Michelson-Inter­ferometers in Richtung der Bewegung der Erde um ein gewisses Stück kontra­hiert wird. Die Idee war, weil sich dieser Arm relativ zum vermeint­lichen „Lichtäther” bewegt, würde dies gewisse Schwankungen der Wechsel­wirkungen zwischen den Atomen des Materials hervor­rufen. Diese physische Kontraktion würde seiner Meinung nach genau der Streifen­verschiebung der Inter­ferenz­streifen entsprechen, sodass deshalb kein Effekt zu beobachten wäre.

Doch „Längenkontraktion” ist keinerlei physische Stauchung, sondern lediglich ein Ergebnis des Messprozesses.

Hierzu betrachtet man die Myonen aus der sekundären Kosmischen Strahlung. Es gibt eine Höhen­strahlung, dessen primärer Anteil aus dem fernen Weltall auf uns zukommt. Das sind haupt­säch­lich Protonen, die über längere Zeit­räume hinweg, durch weit­räumige kosmische Magnet­felder, zu exorbi­tanten Geschwindig­keiten beschleunigt wurden. Sodass diese Photonen Energien haben, die weitaus höher sind, als wir sie jemals in einem Beschleu­niger her­stellen können. Daraufhin haben diese Protonen Energien von bis zu 10¹² GeV (Giga­elektronenvolt). 1 Elektronen­volt ent­spricht der Energie die ein Elektron hat, wenn es innerhalb einer Potential­differenz von einem Volt beschleunigt wird.

Diese primären Protonen fallen im Fall unserer Erde auf die höhere Atmos­phäre ein, und wenn sie zufällig auf ein Stick­stoff­atom Atom der Luft treffen, bilden sich Schauer von neuen Teilchen. Aufgrund der hohen Energie können sich als sekundärer Anteil 10¹¹ Teilchen aus einem Proton bilden. Und diese neuen Teilchen sind dann die Myonen.

Aller­dings sind diese Teilchen, die sich in einer Höhe von 20 km bilden, nur sehr kurz­lebig. Die Halbwerts­zeit der Myonen beträgt gerade einmal 1,52 μs, und sie bewegen sich mit einer Geschwindig­keit von v = 0,9998 · c, also nahezu Licht­geschwindig­keit. Trotz ihrer geringen Halbwerts­zeit kann man die Myonen in nennens­wertem Ausmaß noch auf der Erd­ober­fläche messen. Etwa 1/5 dieser Myonen kommen auf der Erde an. An deren Geschwindig­keit kann das nicht liegen, denn die Teilchen fliegen in 1,52 μs gerade einmal 450 m weit. Theoretisch dürfte gar kein Teilchen auf der Erde ankommen.

Ein Lösungs­ansatz liegt wieder in der Relativitäts­mechanik. Würde man mit einem Myon mitfliegen, dann sähe man die Dicke der Atmosphäre auf ca. 300 m verkürzt. Eine zweite Über­legung ist, wenn man aus Sicht des Ruhe­systems sprich der Erde die Myonen betrachtet, fliegen die Teilchen so schnell, dass aufgrund der Zeit­dilatation die Uhr so langsam geht, dass es aus unserer Sicht den Eindruck hat, als würden die Myonen viel langsamer zufallen und daher schaffen sie es herunter zu kommen.

Eine Paradoxie besteht darin, dass man eine Garage mit einer gewissen Länge betrachtet und ein Auto mit einer gewissen Länge. Das Auto hat eine Ruhe­länge von 6 m und die Garage hat eine Länge von 4 m. Was passiert, wenn dieses Auto mit 5/6 Licht­geschwindig­keit auf die Garage zurast und beim hinein­fahren ganz plötz­lich abbremst. Wenn man aus Sicht der Garage das Auto kommen sieht, wird das Auto auf 3 m kontra­hiert. Aber sobald es steht, hat es wieder seine Ruhe­länge von 6 m.

Wenn man jetzt die Bewegung aus Sicht des Autos betrachtet, kommt zu der eigenen Länge noch die Längen­kontraktion der Garage hinzu. Also eine Situation, die erst recht nicht funktio­nieren wird. Beides scheint auf jeden Fall ein Wider­spruch zu sein. Aber letzten Endes ist es wieder eine Frage der Gleich­zeitig­keit. Und durch die Analyse der Gleich­zeitig­keit lässt sich dieser Wider­spruch aufklären.

In diesem Zusammen­hang stellt sich auch die Frage, was ist die Definition eines starren Körpers? In der Mechanik wurde bereits der starre Körper behandelt. Wenn man ihn an der einen Seite anschiebt, bewegt er sich auch an der anderen Seite. Aller­dings existiert der starre Körper in der Relativitäts­mechanik nicht.

Um das zu veran­schau­lichen, könnte man einen starren Stab von der Erde zum Mond legen. Schiebt man an der einen Seite an, muss gleich­zeitig auf der anderen Seite eine Bewegung zu beobachten sein. Wenn man den starren Körper jetzt durch die Licht­wellen ersetzt, würde das nicht funktio­nieren, weil das Licht für diese Strecke eine halbe Sekunde benötigt.

Derartige Gedanken­spiele sind eine Idealisierung, die nur im Bereich der klassischen Mechanik gilt. Wenn es um größere Geschwindig­keiten geht, und damit um die Bestimmung von Längen, gibt es keine starren Körper.

Wie würde unsere Welt aussehen, wenn man die Licht­geschwindig­keit deutlich reduzieren würde? Zumindest würde man dann die Scheu vor den relativis­tischen Phäno­menen verlieren. Um das Ganze dennoch greif­barer zu machen, wollen wir uns der Trans­formation von Bezugs­systemen zuwenden.

⇦ Kapitel Kapitel ⇨