Wie wir bereits Ansatzweise betrachtet haben, kann die Ausbreitungsgeschwindigkeit elektromagnetischer Wellen im Vakuum mit der Lichtgeschwindigkeit in Zusammenhang gebracht werden. Auf Grundlage zahlreicher Versuche vertrat man schließlich die Auffassung, das auch Licht als elektromagnetische Welle aufgefasst werden kann. Allerdings gilt zu berücksichtigen, das Licht auch Eigenschaften hat, die nicht im Rahmen eines Wellenvorgangs beschrieben werden können.
Bei der bisherigen Betrachtung hat sich ergeben, dass sich elektromagnetische Wellen mit einer gewissen Geschwindigkeit ausbreiten. Somit gilt für das Vakuum:
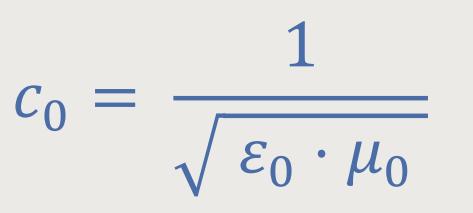
Die Größen ε₀ und μ₀ sind phänomenologische universelle Konstanten, die bei den Grundgesetzen eingeführt wurden. Das ε₀ kennen wir vom Coulomb-Gesetz. Und das μ₀ kennen wir von der Beschreibung des Magnetfeldes eines geradlinigen stromdurchflossenen Leiters.
Aufgrund der experimentellen Ergebnisse konnte man die Vakuum-Lichtgeschwindigkeit c₀ und der magnetischen Feldkonstanten μ₀ festlegen. Sodass sich aus obiger Relation die elektrische Feldkonstante ε₀ ergibt.
Den entsprechenden Wert kennen wir bereits aus der Elektrostatik:
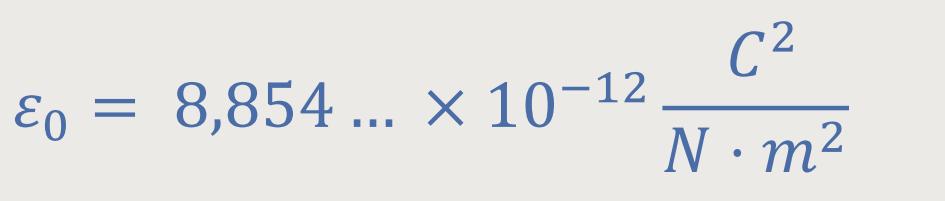
Jetzt stellt sich die angesprochene Frage, relativ zu welchem Bezugssystem wird diese Ausbreitungsgeschwindigkeit gemessen? Die Antwort auf diese Frage führt geradewegs zur Relativistischen Mechanik. Zunächst werden wird einige Grundlagen betrachten.
Die „relativistische Mechanik” ist eine Fortsetzung der Elektrodynamik. Deshalb macht es Sinn, elektromagnetische Felder in verschiedenen Bezugssystemen zu betrachten. Zu Beginn gehen wir von dem einfachen Gesetz für die Lorentz-Kraft aus. Dazu betrachten wir zwei spezielle Situationen.
In „Situation a)” gibt es ein System S, mit einem
elektrischen Feld  und einem
magnetischen Feld
und einem
magnetischen Feld  , sowie eine Ladung
q. Diese Ladung bewegt sich relativ zu dem betrachteten System mit der
Geschwindigkeit
, sowie eine Ladung
q. Diese Ladung bewegt sich relativ zu dem betrachteten System mit der
Geschwindigkeit  . In der
Elektrostatik wurde die Lorentz-Kraft wie folgt definiert:
. In der
Elektrostatik wurde die Lorentz-Kraft wie folgt definiert:
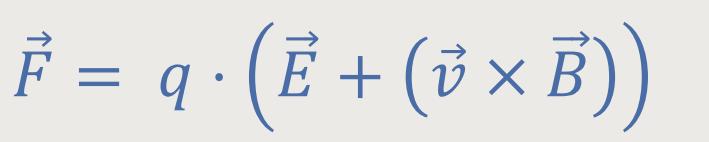
Parallel dazu wird dieser Situation ein System S' gegenüber
gestellt, welches sich mit der gleichen Geschwindigkeit
 relativ zu S
bewegt. Dann sieht es aus der Sicht des Systems S' so aus, als wenn
die Ladung q im System S ruhen würde. Beide
Systeme sind Inertialsysteme, in denen die Kräfte jeweils die gleichen sind. Damit
gilt auch für das System S' die gleiche Kraftwirkung,
allerdings mit einer ruhenden Ladung und einer eigenen elektrischen Feldstärke
relativ zu S
bewegt. Dann sieht es aus der Sicht des Systems S' so aus, als wenn
die Ladung q im System S ruhen würde. Beide
Systeme sind Inertialsysteme, in denen die Kräfte jeweils die gleichen sind. Damit
gilt auch für das System S' die gleiche Kraftwirkung,
allerdings mit einer ruhenden Ladung und einer eigenen elektrischen Feldstärke
 '.
Damit ergibt sich:
'.
Damit ergibt sich:
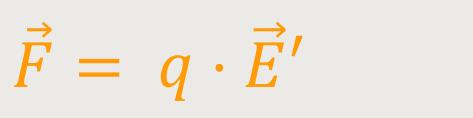
Ein Vergleich beider Systeme fördert folgende Beziehung zutage:
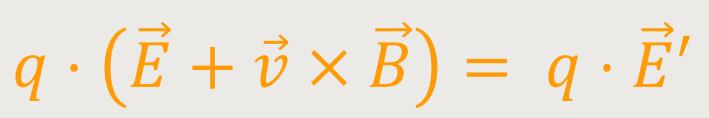
Und damit erhält man für die elektrische Feldstärke
 ' :
' :
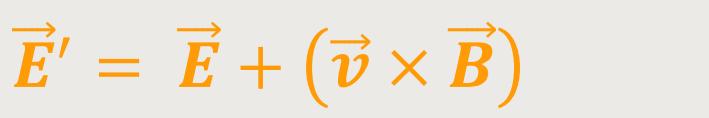
Daraus kann man erkennen, dass die Kraft zwar gleich ist, aber jedes der beiden Systeme hat
demnach ein separates elektrisches Feld. Im System S'
tritt zusätzlich zu  ein
elektrischer Feldanteil
ein
elektrischer Feldanteil
 ×
×
 )
) erwächst.
erwächst.
Wie sieht es jetzt mit der Veränderung des magnetischen Feldes aus?
In „Situation b)” gibt es auch ein System S, mit einer Ladung q auf einem ruhenden Zylinder. In diesem Fall umgibt sich der Zylinder mit einem statischen elektrischen Feld.
Grafik (wird später eingefügt)
Auch hier stellen wir dieser Situation ein System S'
gegenüber, welches sich mit der Geschwindigkeit
 relativ zu S
bewegt, wobei der Geschwindigkeitsvektor parallel zur Zylinderachse liegt.
relativ zu S
bewegt, wobei der Geschwindigkeitsvektor parallel zur Zylinderachse liegt.
Jetzt sieht es aus Sicht des bewegten Systems S' so aus, als
wenn sich die Ladung q in einem Leiter befindet. Und wenn sich
Ladungsträger mit einer gewissen Geschwindigkeit bewegen, ruft dies einen
elektrischen Strom hervor, der wiederum einen magnetischen Feldwirbel
 ' rund um den
Leiter bewirkt. Dieses Feld in Form eines magnetischen Feldwirbels ist definiert als:
' rund um den
Leiter bewirkt. Dieses Feld in Form eines magnetischen Feldwirbels ist definiert als:
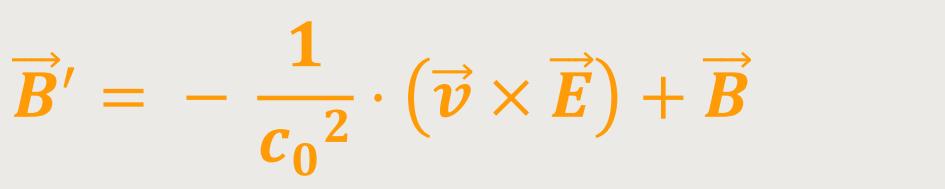
Daraus kann man erkennen, dass im System S' zusätzlich eine
magnetische Flussdichte  auftritt, die aus dem elektrischen Feld
auftritt, die aus dem elektrischen Feld
 im System S
erwächst.
im System S
erwächst.
Die Gegenüberstellung ergibt also, dass der magnetische Feldanteil um einiges geringer ausfällt, als der elektrische Feldanteil. Das heißt, die magnetischen Wirkungen von Strömen sind geringfügig im Verhältnis zu den elektrischen Wirkungen. Denn laut Coulomb-Gesetz sind die Kräfte zwischen den elektrischen Ladungen um ein vielfaches größer als die Magnetfelder.
Das dieser Effekt nicht immer so deutlich zu Tage tritt, liegt in der Regel daran, dass es zum Beispiel in metallischen Leitern immer eine gleich große Menge von entgegengesetzt geladenen Gitteratomen gibt, welche die elektrischen Wirkungen der bewegten Ladungen kompensieren. Und daher machen sich nur noch die magnetischen Wirkungen bemerkbar.
Nun stellt sich die Frage, welche Auswirkungen es hat, wenn man obige Transformation
vom System S zum System S', sprich die
transformierten Felder in die Maxwell-Gleichungen einsetzt. Oder wenn man die
Maxwell-Gleichungen mittels obiger Umrechnungen umformt. Denn als Folge davon
würde man Maxwell-Gleichungen für die Felder
 ' und
' und
 ' erhalten.
' erhalten.
Aber bei entsprechender Vorgehensweise stellt sich heraus, dass bei Anwendung obiger
Transformation die Maxwell-Gleichungen im Fall von veränderten Bedingungen nicht
unverändert bleiben. Sondern es treten vielmehr zusätzliche Terme in den
Gleichungen auf, die proportional zu
Aufgrund der Ausbreitungsgeschwindigkeit elektromagnetischer Wellen lassen sich Lichtwellen als elektromagnetische Wellen darstellen. Insofern geht es bei der Betrachtung auch darum, in welcher Weise die Wellennatur des Lichts in diesem Zusammenhang eine Rolle spielt. Denn es wäre schon ungewöhnlich, wenn die Elektrodynamik nur in einem bestimmten Inertialsystem gilt.
Wenn aber die Ausbreitungsgeschwindigkeit elektromagnetischer Wellen zugleich der Lichtgeschwindigkeit im Vakuum entspricht, muss das Licht einen Wellencharakter haben. Das würde aber bedeuten, in Anlehnung an die Mechanik, dass es doch eigentlich auch ein Trägermedium für eine elektromagnetische Welle bzw. für die Lichtwellen geben müsste.
Man hat bereits vor der Relativitätsmechanik erkannt, dass das Licht ein
transversaler Wellenvorgang ist. Das heißt, man kann das Licht polarisieren
und die  -Vektoren
-Vektoren -Vektoren
-Vektoren
Denn wenn man eine Welle betrachtet, muss es zwangsläufig Auslenkungen eines Mediums geben, typischer Weise elastische Auslenkungen. Die Ausbreitungsgeschwindigkeit erfolgt dann relativ zu diesem Trägermedium. Und wenn es ein solches Trägermedium gibt, muss dieses einen gewissen Bewegungszustand haben, zu dem sich das Licht dann relativ ausbreitet.
Würde man in einem solchen Medium obige Beziehungen zugrunde legen, hätte man ein spezielles Bezugssystem, in welchem die Maxwell-Gleichungen auch gültig wären. Und zwar wäre das ein System, in welchem sich das Lichtmedium, also das Trägermedium der elektromagnetischen Wellen, in Ruhe befände.
Derartige Überlegungen führten dazu, ein solches System näher zu untersuchen.
Und so war es ein gewisser Albert A. Michelson, der das nach ihm benannte Michelson-Interferometer entwickelt hatte und auf die Idee kam, dieses Gerät dazu zu verwenden, ein experimentelles System zu betrachten, welches sich relativ zu einem System bewegt, in dem das Lichtmedium ruht. Also, er wollte herausfinden, wie schnell man sich relativ zu dem Lichtmedium bewegt.
Grafik (wird später eingefügt)
Bei diesem Experiment betrachtet man eine Lichtquelle, dessen Licht auf eine schräg angeordnete Glasplatte, genaugenommen einen halbdurchlässigen Spiegel, trifft. Ein gewisser Anteil tritt durch die Glasscheibe geradewegs hindurch, ein anderer Anteil wird um 90° reflektiert. Beide Strahlen treffen dann ihrerseits auf einen Spiegel, die in gleichen Abständen zum schrägen Spiegel angeordnet sind, und die dieses Licht senkrecht in sich wieder zurückreflektieren.
Von dem reflektierten Licht ist aber nur der Anteil des Strahls von Interesse, der jetzt erneut durch die schräg angeordnete Glasplatte hindurchtritt, bzw. um 90° reflektiert wird. Sodass man letztlich zwei parallel laufende Strahlen hat, die in der gleichen Richtung laufen und schließlich auf einen Betrachtungsschirm auftreffen. Wenn sich das Licht mit der gleichen Geschwindigkeit bewegt, wird es bei gleichen Distanzen zu einer Überlagerung der Wellen kommen.
In diesem Fall werden sich die Wellen konstruktiv überlagern und man erhält einen hellen Fleck. Und wenn jetzt einer der beiden Spiegel um eine viertel Wellenlänge versetzt wird, ist das reflektierte Licht bereits um eine halbe Wellenlänge verschoben. In einem solchen Fall werden sich die auf dem Schirm auftreffenden Wellen gegenseitig auslöschen, sodass jetzt kein Lichtfleck zu sehen ist.
Michelson hatte er die Überlegung, ein solches Interferometer auf der Erde aufzubauen, die sich mit einer nicht unwesentlichen Geschwindigkeit von 30 km/s um die Sonne bewegt. Um zu einem nennenswerten Effekt zu kommen, verlängerte Michelson zum einen die Schenkel zwischen der Glasplatte und den Spiegeln. Des Weiteren drehte er die gesamte Anordnung um 90°, sodass im Wechsel einmal der eine Schenkel in Bewegungsrichtung der Erde steht, und einmal der andere Schenkel.
Das entspricht der Maxwell-Gleichung für das
 -Feld
-Feld
Dadurch sollte sich eine unterschiedliche gesamte Verschiebung der beiden abschließend parallel verlaufenden Strahlen ergeben, und es müsste sich eine entsprechende Veränderung des Interferenzbildes zeigen. Auf diese Weise wollte Michelson die Bewegungsgeschwindigkeit der Erde relativ zum vermeintlichen Lichtäther bzw. Trägermedium mit Hilfe dieses Interferometers untersuchen.
Grafik (Folie) (wird später eingefügt)
Grafik (Folie) (wird später eingefügt)
Trotz des erheblichen Aufwandes zeigte das Experiment keinen Erfolg. Es konnte keine Bewegungsgeschwindigkeit der Erde relativ zu einem Lichtäther beobachtet werden. Die Interferenzen an dem Schirm haben sich nie verändert. Daher musste man die Hypothese von einem Trägermedium des Lichts aufgeben.
Und damit blieb die Frage offen, in was sich die Lichtwellen ausbreiten? Und relativ wozu breiten sie sich Lichtwellen mit Lichtgeschwindigkeit aus?
So war es Albert Einstein der sich fragte, welche Schlussfolgerung muss man aus diesem Ergebnis ziehen? Und in einer Veröffentlichung zur Elektrodynamik bewegter Körper hat er die Grundlage der Speziellen Relativitätsmechanik gelegt. Daraus haben sich zwei Grundgesetze ergeben, die sich aufgrund der experimentellen Grundlagen des Michelson-Experimentes herleiten ließen.
Damit wurde als erstes das Prinzip der Relativität begründet:
In allen Inertialsystemen (unbeschleunigten Systemen) gelten die gleichen
Naturgesetze. Und das beinhaltet auch die Maxwell-Gleichungen.
Als zweites wurde das Prinzip der Konstanz der Lichtgeschwindigkeit festgelegt:
Egal welches Inertialsystem man wählt, die
Vakuum-Lichtgeschwindigkeit hat stets den gleichen Wert.
Somit ist ein Trägermedium für die Beschreibung der elektromagnetischen Wellen nicht erforderlich. Aus diesen zwei Grundprinzipien lassen sich eine Reihe von wichtigen Schlussfolgerungen ziehen. Eine dieser Schlussfolgerung betrifft den Ablauf der Zeit.
⇦ Kapitel Kapitel ⇨
