Ziel ist es, mit einem Trans­formator eine Leistung umzu­setzen bzw. über­tragen zu können. Das erreicht man dadurch, indem an den Klemmen der Sekundär­spule einen Last­wider­stand bzw. ein Verbraucher ange­schossen wird. Dadurch beginnt in der Sekundär­spule ein Strom zu fließen. Daraufhin wird in der Sekundär­spule ein zusätz­licher magne­tischer Fluss auftreten. Dieser zusätz­liche Fluss wird sich inner­halb des Eisen­kerns über den gesamten Trans­formator ausbreiten.

Der magne­tische Fluss in der Primär­spule hängt mit der ange­legten Generator­spannung und der vorge­gebenen Windungs­zahl in dieser Spule zusammen. So erhält man einen Fluss, der unab­hängig von anderen Einflüssen ist und immer konstant bleibt. Der Strom in der Primär­spule wird gerade so groß sein, dass er diesen magne­tischen Fluss hervorruft. Das entspricht dann dem Magneti­sierungs­strom.

Durch den Last­wider­stand wird aller­dings das Gleich­gewicht im Primär­kreis gestört. Wenn die Spannung in der Primär­spule stark genug ist, wird aus dem Generator ein zusätz­licher Wechsel­strom gezogen, der gerade dazu dient, dass der zusätz­liche magne­tische Fluss aus der Sekundär­spule kompensiert wird. Dadurch bleibt der sinusförmige zeit­abhängige magne­tische Fluss in dem Eisen­kern des Trans­formators weiter­hin erhalten.

Wenn man also aus der Sekundär­spule eine Leistung abzieht, holt sich der Trans­formator beim Generator den entspre­chenden Differenz­strom zurück, damit der magne­tische Fluss im Eisen­kern insgesamt unverändert bleibt. Hier hat man die merk­würdige Situation, dass sich der zeitlich veränder­liche magne­tische Fluss gar nicht ändert, wenn man eine Leistung abzieht.

Auf diese Weise lassen sich durch eine entspre­chende Wahl der Windungs­zahl in der Primär­spule und in der Sekundär­spule die Spannungen hoch­trans­formieren oder runter­trans­formieren.

Wie lassen sich Spannungen und Ströme mitein­ander in Beziehung setzen?

Beim Gleichstrom gibt es eine sehr einfache Beziehung zwischen Spannungen und Strömen. Wir kennen es bereits vom Ohm'schen Gesetz:

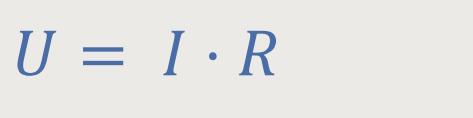
Beim Wechselstrom sieht das ein bisschen kompli­zierter aus, weil es Phasen­verschiebungen geben kann:.

Wenn man jetzt aber U / I dividiert, erhält man eine zeitabhängige Größe. Das ist sehr ungünstig, weil man gerne eine konstante Größe hätte, wie es beim Gleich­strom der Fall ist. Denn selbst bei verschie­denen Spannungen und Strömen bevor­zugt man einen eindeu­tigen Zusammen­hang. Und um das zu vermeiden, gibt es die „komplexen Zahlen”.

Für diejenigen, denen das Thema noch nicht so geläufig ist, sprechen wir kurz über die Euler'sche Relation.

Es zeigt sich, dass eine komplexe e-Potenz, wie folgt geschrieben werden kann:

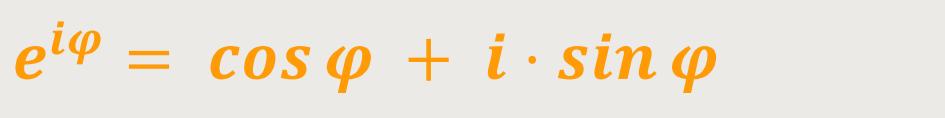
cos φ   ist der Realteil
sin φ   ist der Imaginärteil

Grafik (wird später eingefügt)

In der komplexen Ebene entspricht die x-Achse dem Real­teil Re und die y-Achse dem Imaginär­teil Im. Der Koordinaten­ursprung ist die Zahl Null. Und der Punkt, der in der Zeiger­darstellung mit dem Radius 1 auf einer Kreis­bahn verläuft, wird dann durch die komplexe Zahl e^iφ beschrieben.

Der Punkt am Einheits­kreis läuft in der komplexen Ebene rundherum. Der Betrag einer komplexen Zahl ist die Länge des Zeigers. Und der Zeiger selbst ist der Verbindungs­vektor vom Ursprung bis zu der komplexen Zahl.

Der Betrag der komplexen Zahl ist definiert als:

Der Vorfaktor ist definiert als:

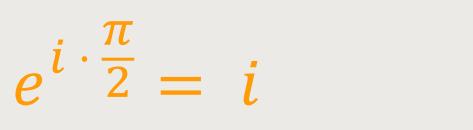
Um Spannungen und Ströme bei Wechsel­strömen in einer über­sicht­lichen Form darstellen zu können, schreibt man diese deshalb in komplexer Schreib­weise auf.

Dann ergibt sich für die Spannung:

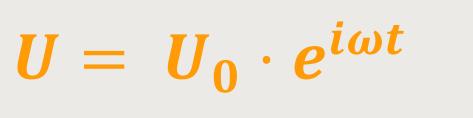
Und für den Strom gilt:

Durch diese Darstellung ergeben sich die tatsäch­lichen physika­lischen Größen für U und I als die Real­teile dieser komplexen Zahlen. Die tatsäch­lichen Spannungen und Ströme sind damit:

Um zu sehen, welchen Vorteil das hat, führt man eine Größe ein, die man die „Impedanz Z” nennt. Die Impedanz ist das, was beim Ohm'schen Gesetz als den Widerstand bezeichnet wird.

Z   ist die komplexe Impedanz

Diese Impedanz ergibt letzt­lich die komplexe Impedanz, weil für die Spannungen und die Ströme auch die komplexen Zahlen einge­setzt werden. Insofern wird jetzt im weiteren Verlauf mit komplexen Zahlen gerechnet und erst am Ende eine Rück­über­setzung in die realen Zahlen erfolgen. Damit erhält man die tatsäch­lichen zeit­lichen Abhängig­keiten der reellen Spannungen und Ströme.

Durch Umstellen ergibt sich zunächst:

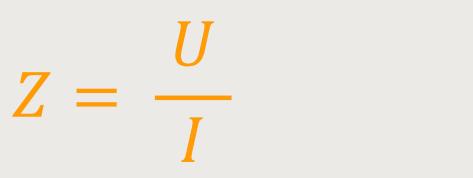
Durch Einsetzen der komplexen Zahlen erhält man:

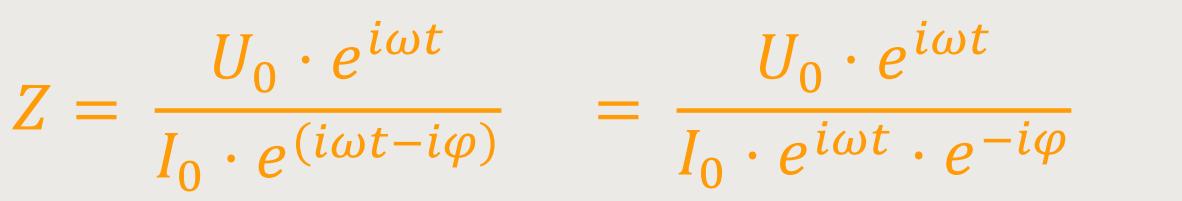
Durch Wegkürzen ergibt sich schließlich:

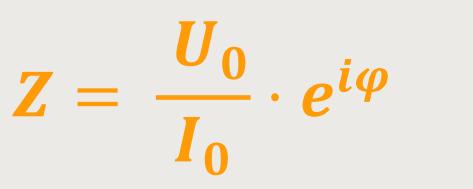
Auf diese Art und Weise erhält man eine Größe, die zeit­unabhängig ist. Diesen Kniff erreicht man nur über die komplexen Zahlen.

Da die komplexe Impedanz das Verhalten eines Wechsel­strom­wider­standes beschreibt, lassen sich nun alle anderen Größen ermitteln. Denn wenn an einen Wechsel­strom­widerstand eine Spannung angelegt wird, fließt ein Strom. Dieser Strom wird im Allge­meinen eine Phasen­verschiebung aufweisen.

Betragsmäßig stellt sich die Impedanz wie folgt dar, wobei e^iφ = 1 ist (s.o.):

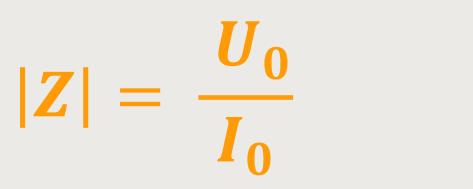
Der Betrag der Impedanz ist somit das Verhältnis der Spannungsamplitude zur Stromamplitude.

Aber mittels der Impedanz lässt sich auch der Phasen­verschiebungs­winkel φ ermitteln:

Hier geht es um den Verschiebungs­winkel der angelegten Spannung und dem dann fließenden Strom. Wenn beide Größen in Phase laufen, ist der Verschiebungs­winkel Null und entspre­chend auch tan φ = 0, und dann ist man wieder zurück beim alten Ohm'schen Gesetz.

Wie sieht das jetzt bei verschiedenen Wechsel­strom­wider­ständen aus?

Da hier die Phasen­verschiebung immer Null ist, gilt entspre­chend für den Widerstand R:

Für eine Spule gilt entspre­chend für die Selbst­induk­tivität L:

Wegen des Induktions­gesetzes kommt hier eine Differen­tiation nach der Zeit vor.

Für einen Konden­sator gilt entspre­chend für C:

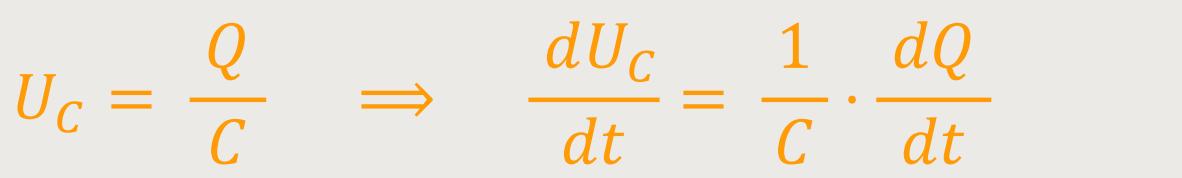
Eine Ände­rung der Ladung des Konden­sators wird dadurch bewirkt, dass in den Zulei­tungen des Konden­sators ein Strom fließt. Daher entspricht die Ladung pro Zeit­einheit dem Strom.

Insofern ergibt sich für den Strom im Konden­sator:

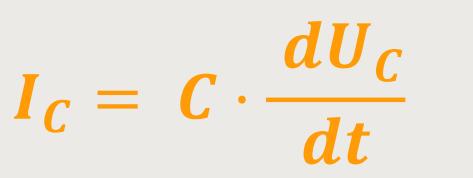
Wie lassen sich mit den obigen Zusammen­hängen die entspre­chenden Impedanzen ausrechnen? Wir werden jetzt noch­mals alle Wider­stände aus Sicht der Impedanz durchgehen.

Die komplexe Impedanz des Widerstandes stellt sich einfach dar als:

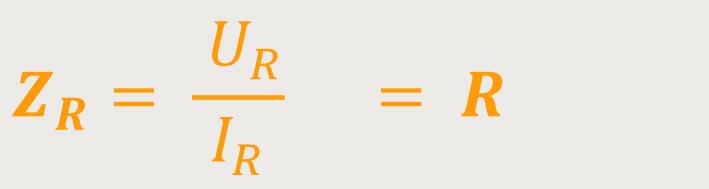
Damit hat der Ohm'sche Wider­stand als komplexe Impedanz den reellen Wider­stand R und ist unab­hängig von der Kreis­frequenz ω des jewei­ligen Wechsel­stroms. Daher gibt es hier keine Phasen­verschiebung.

Da jetzt eine Zeit­abhängig­keit vorhanden ist, muss die Größe des Wechsel­stroms mit berück­sichtigt werden. Der Strom hat eine Cosinus-förmige Zeit­abhängig­keit, die propor­tional zu cos ωt ist, und daher muss zunächst ein Ansatz gemacht werden:

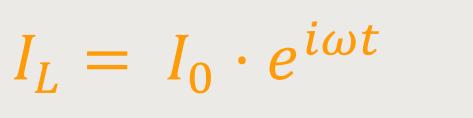
Es ergibt sich zunächst für die Spannung (s.o.):

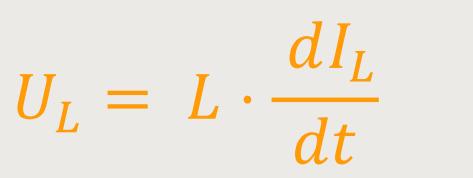
Nun wird der Strom ohne Phasen­verschiebung angesetzt und unter­sucht, was für eine Phasen­verschiebung die Spannung jetzt haben wird.

Wenn man die Exponential­funktion entspre­chend differen­ziert, erhält man erneut eine Exponential­funktion:

Das ergibt sich aus der Phasen­verschiebung der Spannung gegen den Strom.

Daraus folgt, dass sich die komplexe Impedanz für die Spule darstellen lässt als:

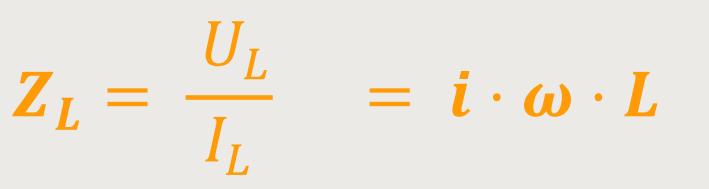
Gleichzeitig ergibt sich aus der Phasen­verschiebung, dass die Spannung U_L dem Strom I_L um π/2 vorauseilt, wobei die Impedanz Z_L propor­tional zur Kreis­frequenz ω ist. Je höher die Frequenz wird, desto größer wird der innere Wider­stand. Und das bezeichnet man als eine „Drosselspule”.

Wie schon des Öfteren erwähnt, wenn eine Spannung an einer Spule anliegt, will ein Strom zu fließen beginnen. Und wenn der Strom zu fließen beginnt, ruft er einen magne­tischen Fluss hervor. Dieser Fluss bewirkt seiner­seits eine Induktions­spannung in der Spule, die so gerichtet ist, dass sie eine Behinderung des Strom­aufbaus bewirken wird. Deshalb wird sich der Strom nur langsam aufbauen können und damit der Spannung hinterher­eilen. Und zwar um den obigen Phasen­verschiebungs­winkel π/2.

Ein solches Additions­theorem von Winkel­funktionen lässt sich verkürzt darstellen.

In diesem Fall setzen wir zunächst die Spannung an und schauen, was der Strom relativ dazu macht:

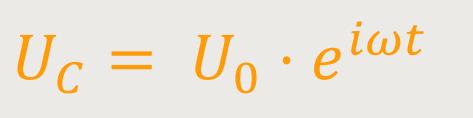
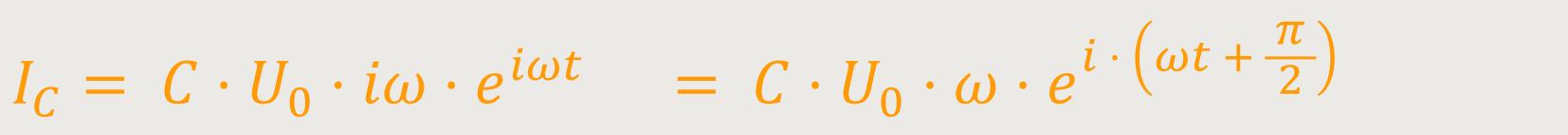
Auch in diesem Fall ergibt sich wieder eine Phasen­verschiebung um π/2.

Daraus folgt, dass sich die komplexe Impedanz für den Konden­sator darstellen lässt als:

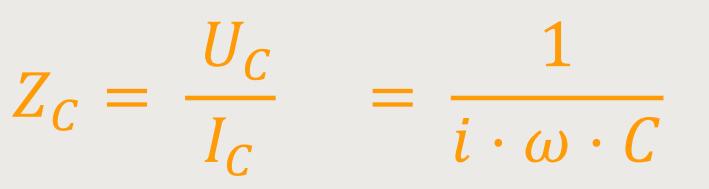
Da man i nicht gerne im Nenner hat, erweitert man zunächst mit i:

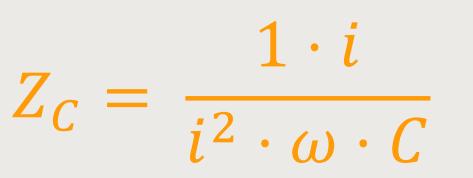
Und da i² = −1 entspricht, lässt sich auch schreiben:

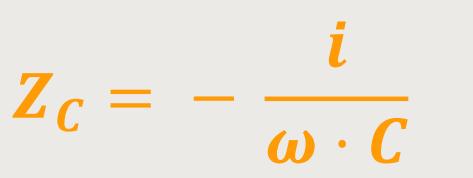
Gleich­zeitig ergibt sich aus der Phasen­verschiebung, dass diesmal der Strom I_C der Spannung U_C um π/2 voraus­eilt, wobei die Impedanz Z_C propor­tional zur Kreis­frequenz 1 / ω ist. Wenn die Frequenz größer wird, wird der Konden­sator immer durch­lässiger.

Damit an den Platten eines Konden­sators über­haupt eine Spannung angelegt sein kann, muss er zuerst aufge­laden werden. Daher muss erst ein Strom fließen, um den Konden­sator aufzu­laden. Dementspre­chend eilt der Strom der Spannung voraus.

⇦ Kapitel Kapitel ⇨