Bei den „elektro­magne­tischen Schwingungen” war es so, dass die Schwingungen länger anhalten und sich die Felder immer ohne zeit­liche Verzögerung über das gesamte betrachtete System ausbreiten.

Grafik (Folie) (wird später eingefügt)

Als Über­leitung betrachten wir zu Beginn gedank­lich einen soge­nannten Hertz'schen Dipol. Darunter versteht man ein Leitungs­stück, in welchem sich Ladungen bewegen können. Wenn sich positive Ladungen zum einen Ende und negative Ladungen zum anderen Ende bewegen, werden sich zwischen den Ladungen außer­halb des Leiters elek­trische Feld­linien ausbilden. Zusätz­lich bilden sich magne­tische Feld­wirbel, die sich 90° versetzt dazu anordnen, und diese umkreisen den strom­durch­flossenen Dipol.

Wenn die Ladungen an den Enden des Leiters angekommen sind, kommt der Strom zum Erliegen. Es gibt zwar nach wie vor die elek­trischen Feld­linien, aber die magne­tischen Feld­linien haben sich ausge­breitet, sodass es jetzt unmittelbar um den strom­durch­flossenen Dipol keinen magne­tischen Feld­wirbel mehr gibt. Erst wenn die Schwingung wieder zurück­läuft, kommt es zu einem Strom­fluss in die entgegen­gesetzte Richtung.

Der Strom wird maximal, wenn die Ladungen in der Mitte des Leiters zusammen­treffen, sodass sich jetzt die elek­trischen Feld­linien nach außen aus­breiten. Als Folge kommt es zu keinem elek­trischen Feld mehr, denn die elek­trischen Feld­linien werden quasi vom Leiter abge­stoßen und schließen sich. Sodass im Nahfeld des Dipols kein elek­trisches Feld mehr vorhanden ist. Jetzt haben wir in der Gegen­richtung einen magne­tischen Feld­wirbel.

Anschlie­ßend beginnt der Zyklus wieder von vorne, und wir haben somit einen Oszillator der im Wechsel elek­trische und magne­tische Feld­linien erzeugt, die sich jeweils in entgegen­gesetzte Richtung zu den vorherigen ausbilden und anschlie­ßend vom Dipol ablösen und ausbreiten.

Wie lassen sich aber nun diese Wellen im Detail charakte­risieren?

Hierzu rufen wir uns noch­mals die Beschrei­bung einer Welle aus der Mechanik in Erinnerung, nämlich als einen räum­lich und zeit­lich periodischen Vorgang. Die mecha­nische Welle wurde als eine Auslenkung abhängig von einer Orts­koordinate und der Zeit definiert:

u₀   ist die Amplitude
ω   ist die Kreis­frequenz
k   ist die Wellenzahl

Für die Kreis­frequenz lässt sich auch schreiben:

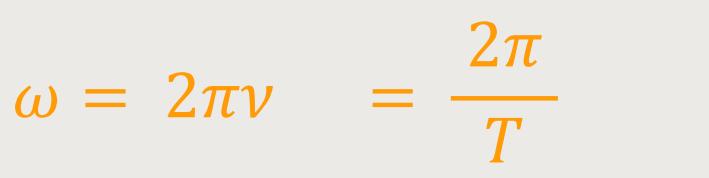
T   ist die Schwingungs­dauer

Für die Wellen­zahl lässt sich auch schreiben:

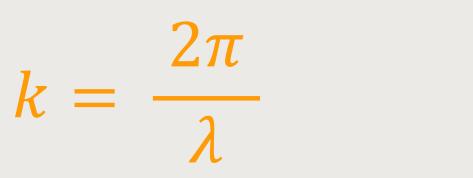
λ   ist die Wellen­länge

Da sich die Wellen natür­lich 3-dimensional ausbreiten, muss man den Ansatz verallge­meinern. Insofern ergibt sich für die mecha­nische Welle im 3-dimsionalen Raum:

  ist der Wellen­zahl­vektor im 3D-Raum

In der Mechanik wurde die Größe der Auslenkung u zweimal nach dem Ort oder alter­nativ zweimal nach der Zeit abge­leitet. Daraus ergab sich folgender Zusammen­hang:

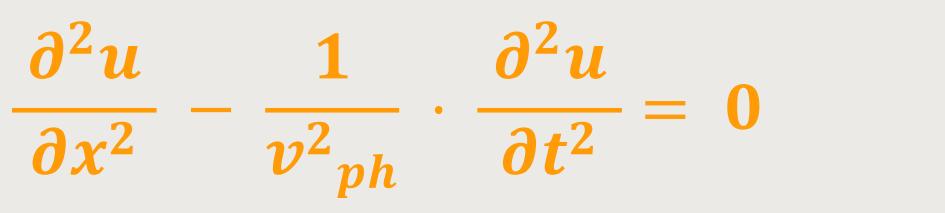
Diese Differential­gleichung nennt man auch die Wellen­gleichung (1-dimensional).

Wobei für die Phasen­geschwindig­keit gilt:

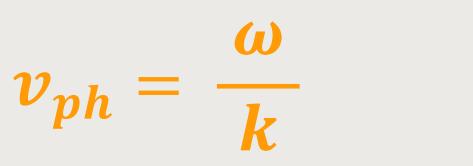
Die Phasen­geschwindig­keit wird bei einer der­artigen Welle definiert als die Ausbreitungs­geschwindig­keit von Punkten konstanter Phase .

Und wenn man entspre­chend einsetzt erhält man:

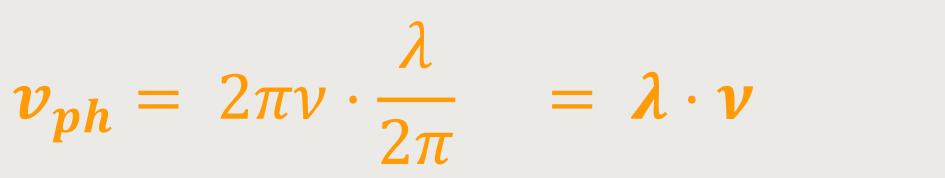
Diese Beziehung sagt aus, dass ν (nu) die Anzahl der Schwingungen pro Zeit­einheit ist, und λ die Aus­breitung für eine Schwingung ist. Daher entspricht λ · ν der Aus­breitung während der Zeit­einheit.

Nun lässt sich obige Differential­gleichung auch für den 3-dimensio­nalen Raum darstellen:

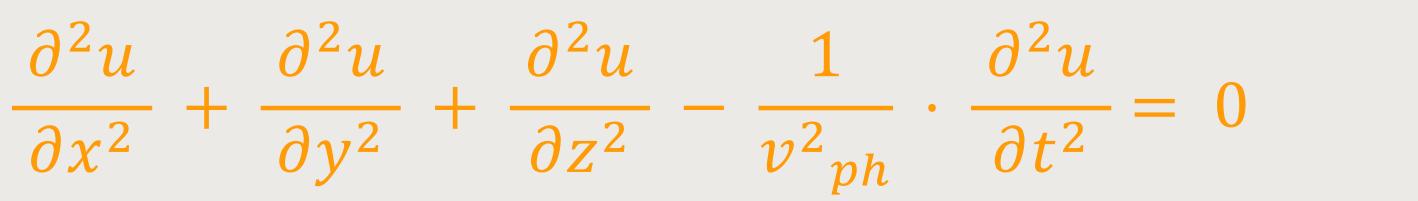
Die erste additive Gruppe fasst man auch gerne zum Laplace-Operator Δu zusammen. Daher ergibt sich in verkürzter Schreib­weise:

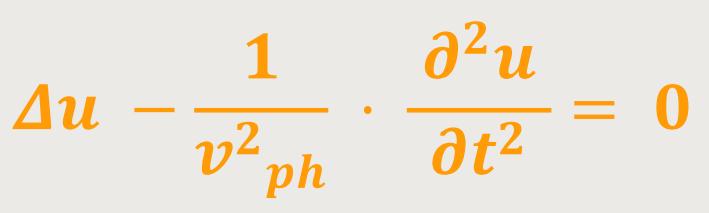
Diese Differential­gleichung nennt man jetzt die Wellen­gleichung (3-dimensional).

Diese kurze Zusammen­fassung wurde zum Teil bereits in der Mechanik behandelt.

Jetzt interessiert uns natür­lich auch, wie sich das Ganze auf die „elektro­magne­tischen Wellen” über­tragen lässt. Grund­lage für die nach­folgenden Über­legungen sind die bereits bekannten Maxwell-Gleichungen.

Hierzu betrachten wir einen Raum, in welchem es weder freie Ladungen noch freie Ströme gibt. Hierfür bietet sich das Vakuum an.

Und das bedeutet zunächst als Ausgangs­situation:
ρ = 0, = 0

Daraus folgt wiederum, dass div = 0 und div = 0.

Wie sieht es nun konkret mit der Rotation des Systems aus? In Anlehnung an die Maxwell-Gleichungen ergibt sich:

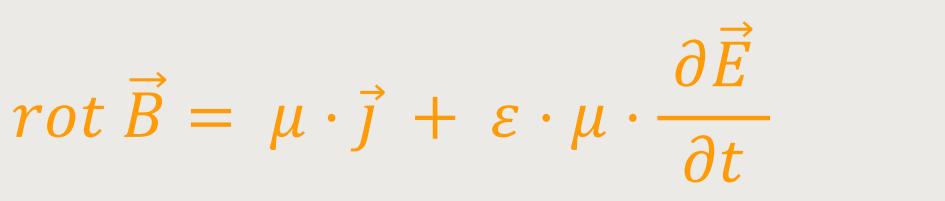
Das ist die Maxwell-Gleichung für das -Feld, wenn dielektrische und magne­tische Medien vorhanden sind.

Nun kamen einige scharf­sinnige Personen auf die Idee, von dieser Gleichung nochmals die Rotation zu bilden. Dann ergibt sich, wobei der erste Term in obiger Grund­gleichung wegfällt, weil gleich Null ist:

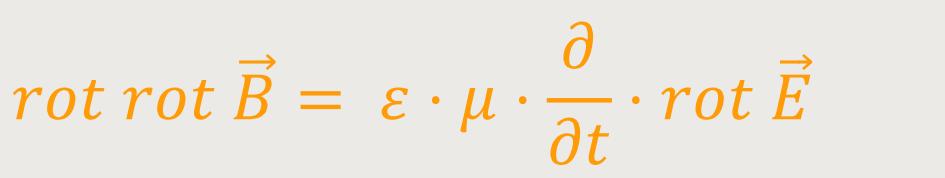
Für rot rot kann man aber auch schreiben:

Wenn man das entspre­chend einsetzt, erhält man:

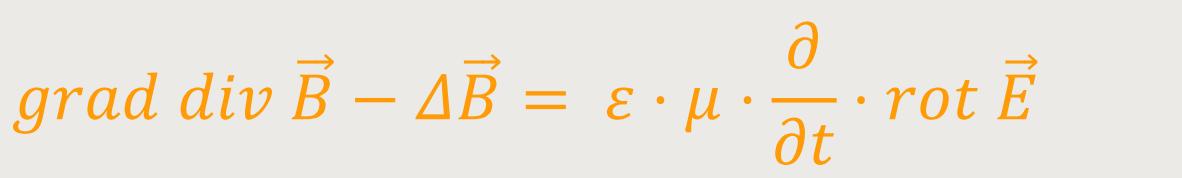
Des Weiteren wissen wir aus der 4. Maxwell-Gleichung:

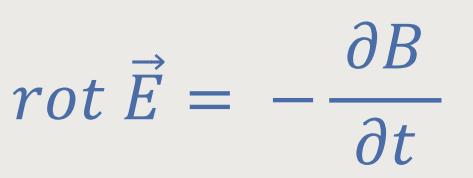
Da div = 0 ist, fällt auf der linken Seite der erste Term weg. Und wenn man auf der rechten Seite entspre­chend einsetzt, erhält man:

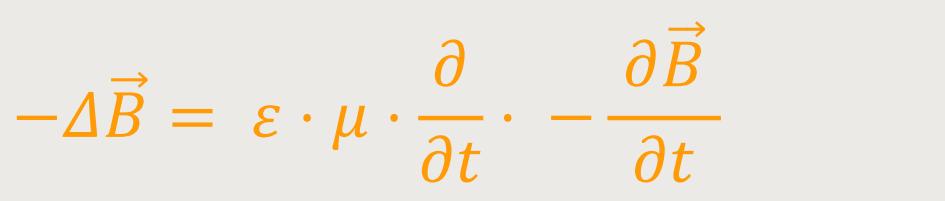
Durch Umstellen ergibt sich dann:

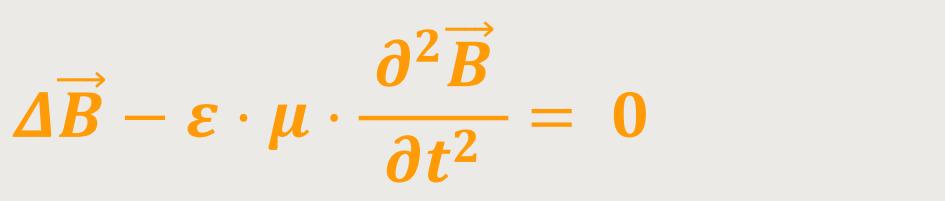
Hier wurden letzt­lich nur verschie­dene Maxwell-Gleichungen ineinander einge­setzt. Als Ergebnis ist zu erkennen, dass das -Feld einen Wellen­charakter aufweist. Es ergibt sich eine vektorielle Auslen­kung in drei Dimensionen, die sich zudem wellen­haft ausbreitet.

Gleich­zeitig ergibt sich durch einen Vergleich mit der Wellen­gleichung für die Phasen­geschwindig­keit:

Wenn man jetzt nach gleicher Vorgehens­weise wie oben die noch­malige Rotation von der Gleichung für rot ableiten würde, kommt haargenau das Gleiche heraus, jetzt aller­dings für das -Feld:

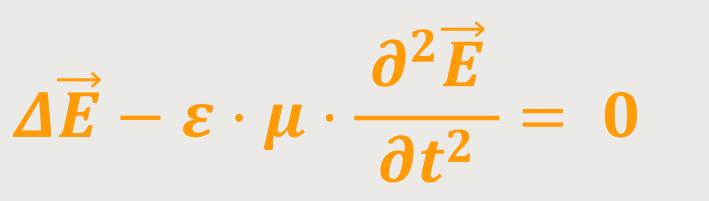
Also, das -Feld und das -Feld weisen jeweils einen Wellen­charakter mit obiger Phasen­geschwindig­keit auf.

Und wenn man das Ganze in unserer Betrachtung auf ein Vakuum-Medium anwendet, dann gilt:

Und das bedeutet jetzt für die Phasen­geschwindig­keit im Vakuum:

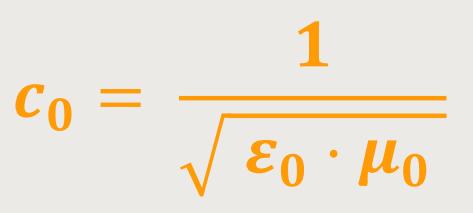
Das ist die Ausbreitungs­geschwindig­keit elektro­magne­tischer Wellen im Vakuum.

Oder anders ausge­drückt, das ist innerhalb gewisser Fehler­grenzen die Vakuum-Licht­geschwindig­keit.

Wenn man in diesem Zusammen­hang von der Phasen­geschwindig­keit spricht, stellt sich jedoch immer die Frage, relativ zu welchem Bezugs­system. Denn in der Definition sind nur Natur­konstanten enthalten. In dem Forma­lismus ist kein Ausdruck für eine Relativ­geschwindig­keit enthalten. Und auch in den Maxwell-Gleichungen gibt es an keiner Stelle einen Bezug auf ein speziell fest­gelegtes Bezugs­system.

Dieser Über­legung werden wir im nächsten Kapitel auf den Grund gehen.

⇦ Kapitel Kapitel ⇨