In Verbindung mit den elektro­magne­tischen Schwingungen, sprich bei der Wechsel­strom­lehre ist es von Vorteil, insbesondere bei den Wechsel­strömen und den Wechsel­strom­widerst­änden, die jewei­ligen Wider­stände durch komplexe Impedanzen darzu­stellen. Des Weiteren lassen sich die Spannungen und Ströme mit ihren perio­dischen Zeit­abhängig­keiten als komplexe e-Potenzen darstellen. Dadurch können die tatsäch­lichen Spannungen und Ströme als die Real­teile dieser komplexen Zahlen dargestellt werden.

Im vorherigen Kapitel haben wir den Forma­lismus zu den komplexen Impedanzen für den Ohm'schen Wider­stand, die Spule und den Konden­sator betrachtet. Jetzt wollen wir diese komplexen Größen und ihre Zusammen­hänge in der komplexen Ebene visuali­sieren. Dazu verwendet man die sogenannte Zeiger­darstellung, die den Vorteil hat auch auf­wendigere Schaltungen, bei denen mehr als nur ein Wechsel­strom­widerstand enthalten ist, über­sichtlich darzustellen.

Die Zeiger­dar­stellung ist bereits ein geläufiges Mittel aus der Mechanik. Wenn man zum Beispiel Schwingungen mit komplexen e-Potenzen in einer Grafik darstellt, dann geht es um einen grafischen Zeiger, der sich während der mechan­ischen Schwingung im Gege­nuhr­zeiger­sinn in der komplexen Ebene bewegt. Der sogenannte Real­teil entspricht der waage­rechten x-Komponente. Und im Laufe der Zeit, wandert die waage­rechte Komponente während der Rotation des Zeigers hin und her, und das entspricht der Schwingung, um die es letztlich geht.

In ähn­licher Weise lässt sich diese Zeiger­darstellung auch im Zusammen­hang mit der Wechsel­strom­lehre anwenden.

Grafik (wird später eingefügt)

In der komplexen Ebene lässt sich sowohl die Spannung U als auch den Strom I als komplexe Zahlen darstellen.

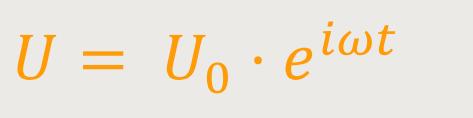
Der Winkel zwischen den beiden Zeigern entspricht der Phasen­verschiebung φ. Und das Ganze rotiert mit der Winkel­geschwindig­keit ω um den Koordinaten­ursprung. Die Winkel­geschwindig­keit oder Kreis­frequenz ist definiert als:

ν (nu)   ist die Frequenz in Schwingungen pro Sekunde

Oder anders ausgedrückt:

T   ist die Schwingungs­dauer einer einzelnen Schwingung

Wenn 2π der volle Winkel im Bogenmaß ist, dann ist 2π / T genau die Winkel­geschwindig­keit. Und daher ist die Kreis­frequenz auch die Winkel­geschwindig­keit der Drehung der Zeiger­anordnung in der komplexen Ebene. Und die Beträge der Zeiger sind die Amplituden der entspre­chenden physika­lischen Größen.

Da es im Allge­meinen eine Phasen­verschiebung zwischen der Spannung und dem Strom gibt, zeigen die jewei­ligen Zeiger in unter­schied­liche Richtungen. Dennoch handelt es sich bei den Zeigern zueinander um eine starre Anordnung, die in der komplexen Ebene mit der Winkel­geschwindig­keit rotiert.

Wir werden nun in unter­schied­lichen Zeiger­darstellungen die Lage der Spannungs- und Strom­zeiger­anordnung bei einem Ohm'schen Wider­stand, einer Spule und einem Konden­sator grafisch darstellen.

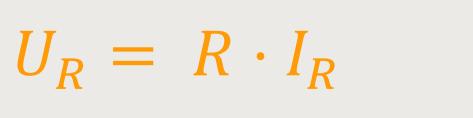
Grafik (wird später eingefügt)

Gemäß der Grafik sind beide Zeiger parallel, sodass sich keine Phasen­verschiebung ergibt.

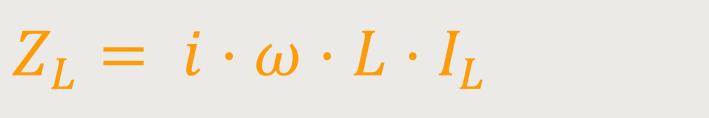
Grafik (wird später eingefügt)

Gemäß der Grafik ergibt sich eine Phasen­verschiebung von π / 2, sodass die Spannung U_L dem Strom I_L um π / 2 vorauseilt.

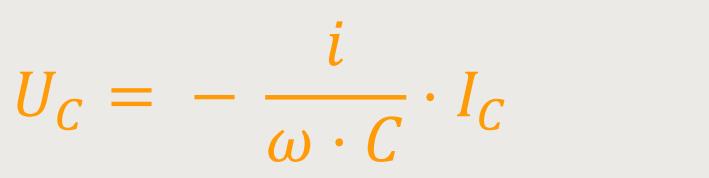
Grafik (wird später eingefügt)

Gemäß der Grafik ergibt sich eine Phasen­verschiebung von π / 2, sodass hier der Strom I_C der Spannung U_C um π / 2 vorauseilt.

Neben diesen Standard-Zeigerdiagrammen wollen wir noch etwas komplexere Zeigerdarstellungen betrachten.

Mit der Beziehung U = Z · I gibt es eine formale Analogie zur Gleich­strom­lehre, bei der die Beziehung U = R · I gilt. In Verbindung mit den Gleich­strömen gelten die Kirchhoff'schen Regeln. Diese Regeln, sprich die Knotenregel und die Schleifenregel, lassen sich formal auch auf die Wechsel­strom­lehre über­tragen. Voraus­setzung dafür sind die jewei­ligen Größen in komplexer Schreib­weise bzw. die Wider­stände in Form von komplexen Impedanzen.

Grafik (wird später eingefügt)

Betrachten wir gedank­lich einmal eine Serien­schaltung. Ausge­hend von einer Wechsel­spannungs­quelle befinden sich in dem Strom­kreis ein Wider­stand R, eine Spule L und ein Konden­sator C, alle in Serie geschaltet. Die Spannung U teilt sich nun auf in die Spannung am Wider­stand U_R, die Spannung an der Spule U_L, und die Spannung am Konden­sator U_C.

Insofern gilt für die Gesamt­spannung:

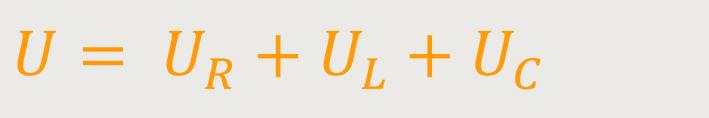
Die Gesamt­impedanz dieser Anordnung ist die Summe der einzelnen in Serie geschalteten Widerstände:

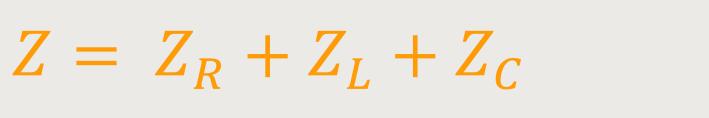
Durch Einsetzten ergibt sich entspre­chend:

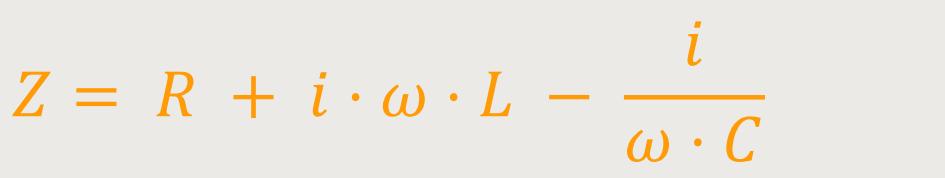
Betragsmäßig stellt sich die Impedanz wie folgt dar:

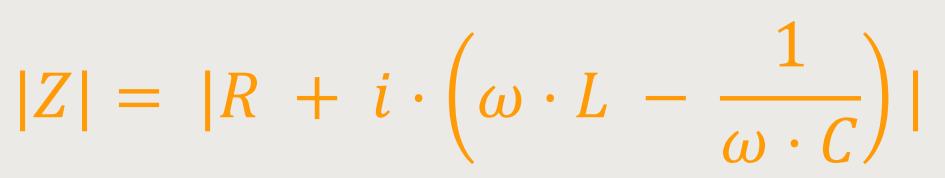
Da das R für den Realt­eil steht, und der Inhalt der Klammer für den Imaginär­teil, lässt sich der Betrag auch darstellen als:

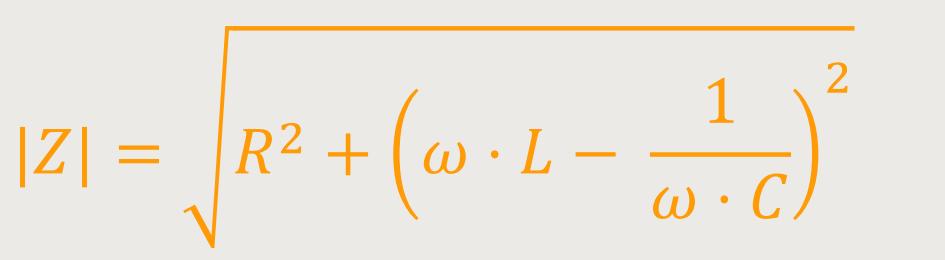
Darunter versteht man auch das Verhältnis der Amplituden:

Das Verhältnis der Impedanz vom Imaginär­teil zum Real­teil entspricht:

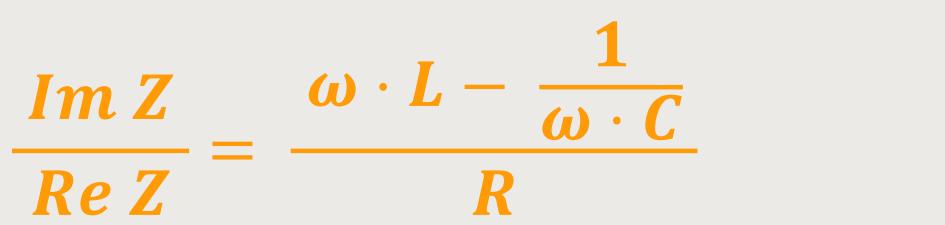
Und das entspricht dem Phasen­verschiebungs­winkel tan φ.

Damit erhalten wir zwei wichtige Aussagen über das Verhalten eines Wechsel­strom­kreises.

Als Zeiger­diagramm sieht das dann wie folgt aus:

Grafik (wird später eingefügt)

Der eine Strom­zeiger I gilt für alle drei Schalt­elemente. Der Spannungs­zeiger des Wider­standes U_R verläuft parallel dazu und entspricht der Ampli­tude U_₀R. Der Spannungs­zeiger der Spule U_L ist gegen den Uhrzeiger­sinn um 90° versetzt und entspricht der Amplitude U_₀L. Hier eilt die Spannung dem Strom voraus.

Je größer die Kreis­frequenz ist, desto größer wird bei einem bestimmten Strom die an der Spule anlie­gende Spannung sein. Und damit wird auch der Wider­stand in der Spule größer. Der Spannungs­zeiger der Spule U_C ist mit dem Uhrzeiger­sinn um 90° versetzt und entspricht der Amplitude U_₀C. Hier eilt die Spannung dem Strom hinter­her. Mit zuneh­mender Frequenz wird der Wider­stand im Konden­sator immer geringer und die Spannung wird im kleiner werden.

Aus dem Zeiger­diagramm der Serien­schaltung ergibt sich die Gesamt­spannung U, dessen Zeiger­position sich aus den anderen Zeigern ergibt, mit einem entspre­chenden Phasen­verschiebungs­winkel φ.

Wenn in einer solchen Schaltung der Wider­stand sehr klein ist, ist die Gesamt­spannung nahezu Null. In diesem Fall spricht man von einer „Spannungs­resonanz” bzw. hier von einer „Serien­resonanz”.

Dem werden wird jetzt die Parallelschaltung gegenübergestellt.

Grafik (wird später eingefügt)

Jetzt betrachten wir gedank­lich eine Parallel­schaltung. Ausge­hend von einer Wechsel­spannungs­quelle befinden sich in dem Strom­kreis ein Wider­stand R, eine Spule L und ein Konden­sator C, alle parallel geschaltet. Während bei der Serien­schaltung durch alle Bauteile der gleiche Strom durchge­flossen ist, liegt jetzt an allen Bau­teilen die gleiche Spannung U an. Nun haben wir einen Gesamt­strom I, der sich aufteilt in einen Strom am Wider­stand I_R, einen Strom an der Spule I_L, und einen Strom am Konden­sator I_C .

Nun gilt für den Gesamt­strom:

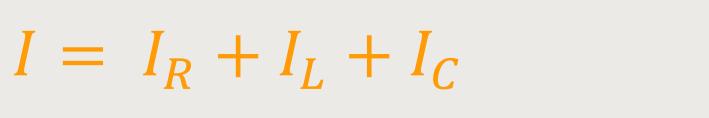
Gemäß der Kirchhoff'schen Knotenregel addieren sich bei parallel geschal­teten Wider­ständen, jetzt die Reziprok­werte. Die Gesamt­impedanz der Parallel­schaltung ist die Summe der einzelnen Kehrwerte:

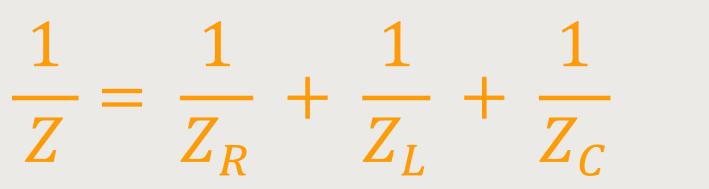
Durch Einsetzten ergibt sich entspre­chend:

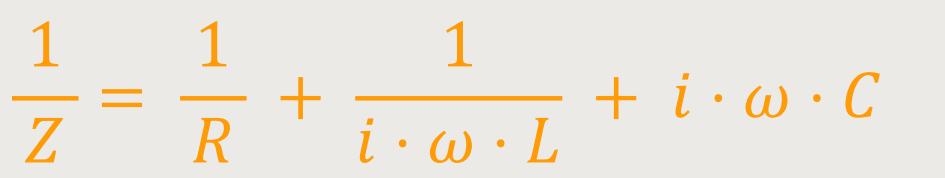
In einem Zwischen­schritt werden die Brüche erweitert, um nur den Betrag von Z zu erhalten. Dies lässt sich an folgendem Beispiel verdeutlichen:

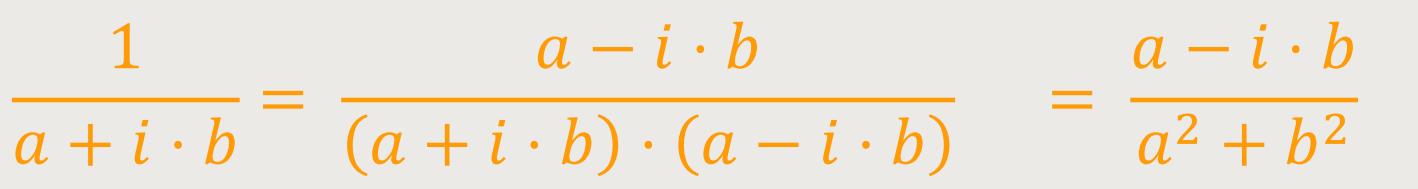
Auf diese Weise lässt sich bei komplexen Zahlen ein Reziprok­wert in eine Zahl mit einem Real­teil und einem Imaginär­teil umwandeln.

Wenn man das entspre­chend auf obige Brüche anwendet, stellt sich die Impedanz jetzt betrags­mäßig wie folgt dar:

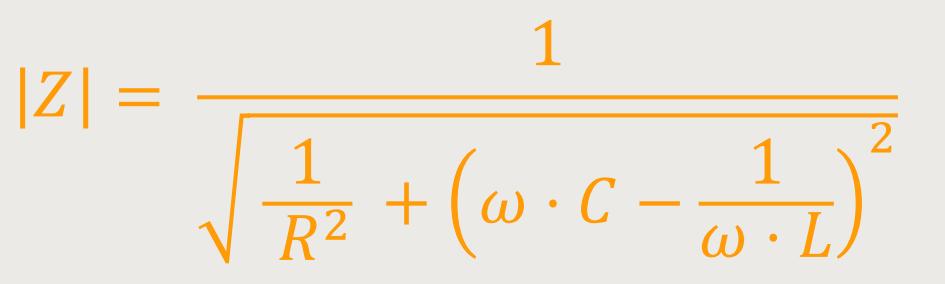
Darunter versteht man auch hier das Verhältnis der Amplituden:

Und der Phasen­verschiebungs­winkel tan φ lässt sich jetzt ausdrücken als:

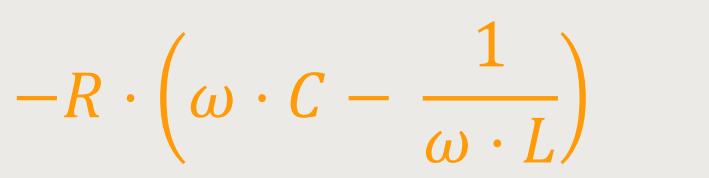
Das entspre­chende Zeiger­diagramm sieht dann wie folgt aus:

Grafik (wird später eingefügt)

Hier gilt jetzt der Spannungs­zeiger U für alle drei Schalt­elemente. Der Strom­zeiger des Wider­standes I_R verläuft parallel dazu und entspricht der Amplitude I_₀R. Der Strom­zeiger der Spule I_L ist mit dem Uhrzeiger­sinn um 90° versetzt und entspricht der Amplitude I_₀L. Hier eilt die Spannung dem Strom nach. Der Strom­zeiger der Spule I_C ist gegen den Uhrzeiger­sinn um 90° versetzt und entspricht der Amplitude I_₀C. Hier eilt der Strom der Spannung voraus.

Aus dem Zeiger­diagramm der Parallel­schaltung ergibt sich der Gesamt­strom I, dessen Zeiger­position sich aus den anderen Zeigern ergibt mit einem entspre­chenden Phasen­verschiebungs­winkel φ.

Wenn in einer solchen Schal­tung die Kapa­zität und die Indukti­vität wieder gleiche Werte annehmen, ist der Gesamt­strom nahezu Null. In diesem Fall spricht man von einer „Strom­resonanz” bzw. hier von einer „Parallel­resonanz”.

Also, wenn man beide Schal­tungen gegen­über stellt, spricht man entweder von einem Schwing­kreis oder einem Sperr­kreis.

⇦ Kapitel Kapitel ⇨