Im letzten Kapitel wurden unter anderem die Resonanz­erscheinungen bei Serien­schaltungen und Parallel­schaltungen ange­sprochen. Es hat sich gezeigt, wenn in Verbindung mit Wechsel­strom mehrere Spulen und Konden­satoren in Serie geschaltet werden oder alter­nativ parallel ange­ordnet sind, dass es zu Resonanz­erscheinungen kommen kann. Eine große Rolle spielt hierbei eine bestimmte „Resonanz­frequenz”.

Im Fall der Serien­schaltung war es so, dass die Spannungen bei einer Resonanz­frequenz ω_₀ bei der Spule und dem Konden­sator genau gegen­phasig und mit gleicher Amplitude ablaufen. Daher bleibt in Summe für den Serien­strom­kreis keine Spannung mehr übrig, und die Serien­schaltung wird damit durch­lässig. Trotz­dem wird es an den einzelnen Bau­teilen, sprich der Spule und dem Konden­sator, mitunter zu ganz beträcht­lichen Spannungen kommen.

Und bei der Parallel­schaltung war es so, dass hier die Ströme bei einer Resonanz­frequenz ω_₀ genau gegen­phasig und mit gleicher Amplitude bei der Spule und Konden­sator auftreten. Insofern werden sich in Summe die Ströme entspre­chend weg­kompen­sieren, sodass der ganze Parallel­strom­kreis undurch­lässig wird. Durch den Parallel­strom­kreis tritt in diesem Fall gar kein Strom mehr durch.

Nur inner­halb des Parallel­kreises tritt mitunter eine erheb­liche Schwingung der Ströme im Bereich der Bau­teile auf, sprich der Spule und dem Konden­sator. Es läuft der Strom nur rund­herum, aber nicht durch die beiden Bau­teile hin­durch. So etwas nennt man auch einen „Schwing­kreis”, der auch wieder bei einer bestimmten Resonanz­frequenz auftritt.

Diese Resonanz­frequenz wurde definiert als:

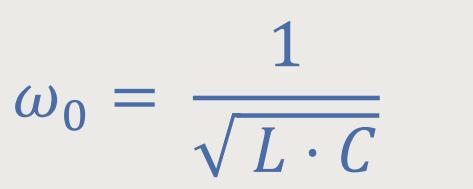
Diese Frequenz gilt sowohl für die Serien­resonanz bzw. Spannungs­resonanz, als auch für die Parallel­resonanz bzw. Strom­resonanz.

Grafik (wird später eingefügt)

Die Resonanz lässt sich auch noch aus einem anderen Blick­winkel betrachten, wenn es zum Beispiel um einen ungedämpften Schwing­kreis geht. Hierzu denken wir uns einen Strom­kreis, mit einer Spule auf der einen Seite und einem Konden­sator auf der anderen Seite. Bei der Spule gibt es eine Selbst­induktivität L und bei dem Konden­sator die Kapazität C.

Jetzt geht es darum, wie sich bei einem solchen L-C-Kreis der Strom als Zeit­funktion ausrechnen lässt.

Wir erinnern uns, die Induktions­spannung an der Spule wurde definiert als:

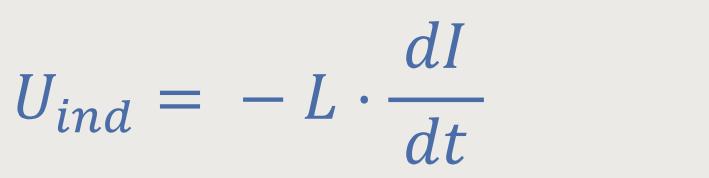
Das gilt für den Fall, dass sich der Strom im Laufe der Zeit ändert, ansonsten ist die Spannung U_ind gleich Null.

Bei zeitlicher Änderung tritt dann auf der Konden­sator­seite ein Spannungs­abfall ein. Und das war laut Definition nichts anderes als:

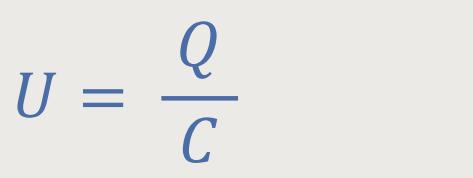
Und damit erhält man auf Grundlage der Kirchhoff'schen Schleifenregel:

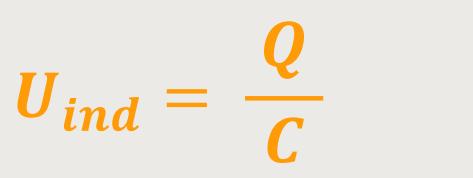
In einen solchen Schwing­kreis ist die Summe aller Spannungen gleich Null, und damit erhält man durch Einsetzten:

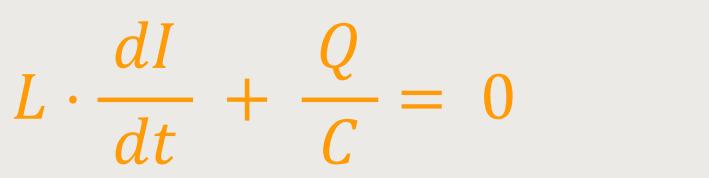
Nun muss der Strom im Schwing­kreis in Form einer Differential­gleichung dargestellt werden. Deshalb differenziert man noch einmal nach der Zeit, indem beide Terme entspre­chend erweitert werden:

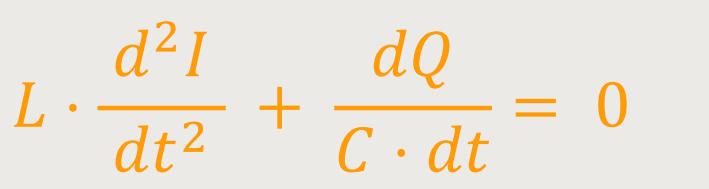
Da aber dQ / dt = I entspricht, kann man vereinfacht schreiben:

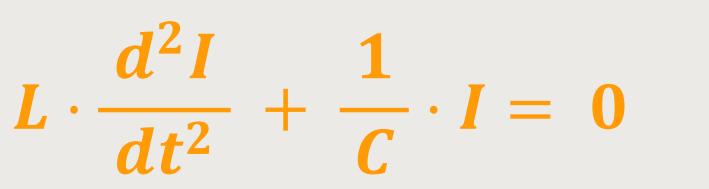
Das ist die Differential­gleichung einer ungedämpften Schwingung.

Nun lässt sich diese Beziehung mit einem komplexen Lösungs­ansatz lösen.

Zunächst wird der gesuchte Strom in Form einer Amplitude angesetzt:

Dann benötigt man noch die zweite Ableitung von I:

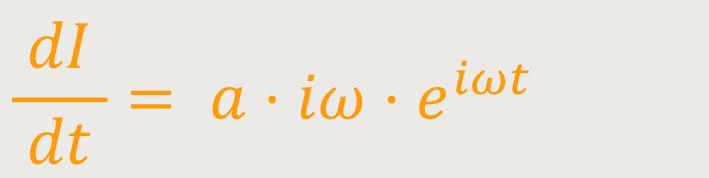
Und wenn man nochmal differenziert, ergibt sich:

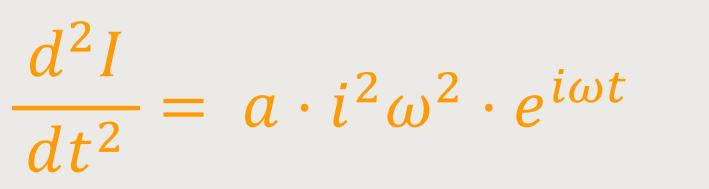
Da i² = −1 entspricht, kann man auch schreiben:

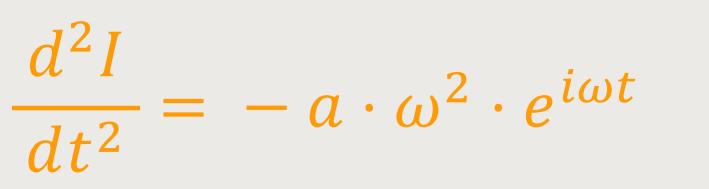
Durch Einsetzen erhält man jetzt:

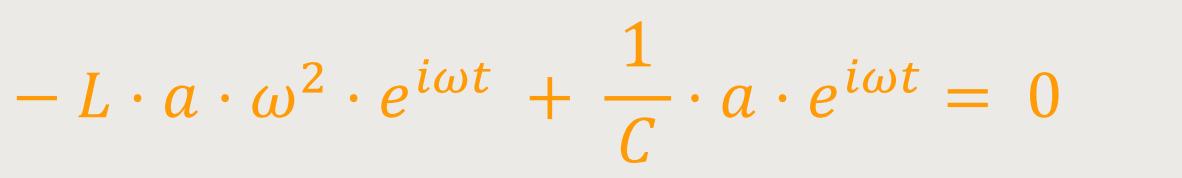
Wie man sieht, lässt sich jeweils die Amplitude und die komplexe Einheit nach der Zeit e^iωt wegkürzen. Somit bleibt nur noch übrig:

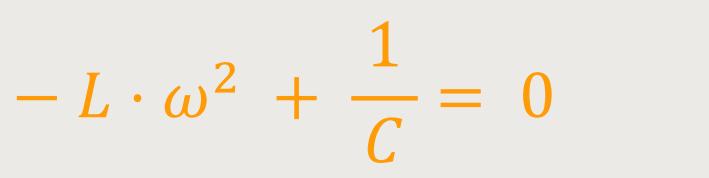
Und damit erhält man eine einfache Beziehung:

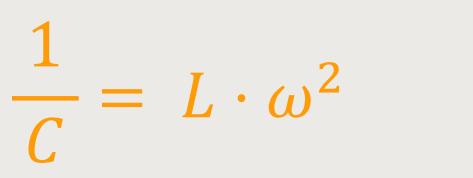
Durch Umstellen erhält man nun genau das, was bereits oben für die Resonanz­frequenz definiert wurde:

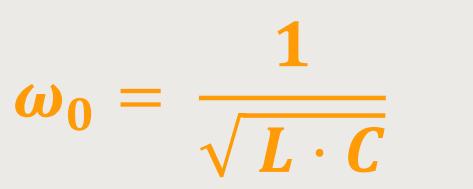
Das ist jetzt die Kreis­frequenz des unge­dämpften Schwing­kreises.

Für genügend kleine Indukti­vitäten und Kapazitäten können dabei durchaus sehr hohe Frequenzen heraus­kommen. In diesem Fall wären die Annahmen der Wechsel­strom­lehre, nämlich dass es zu keiner Wellen­ausbreitung kommt, nicht mehr zutreffend.

Grafik (Folie) (wird später eingefügt)

Bei einem „Schwingkreis” geht der Strom periodisch hin und her. Zu einem bestimmten Zeit­punkt, wenn der Konden­sator zum Beispiel voll aufge­laden ist, wird der Strom gerade Null sein. Anschlie­ßend wird der Konden­sator beginnen, sich über die Spule zu entladen. Als Folge davon wird durch die Spule ein Strom fließen und es wird sich in der Spule ein magne­tisches Feld aufbauen. Nach einer gewissen Zeit wird dann der Konden­sator voll­ständig entladen sein.

Die Spule hat jetzt aber das Bestreben, den Strom­fluss aufrecht zu erhalten. Denn eine Verän­derung des magne­tischen Flusses in der Spule führt wiederum zu einer Induktions­wirkung in der Spule. Insofern wird die Spule jetzt als Spannungs­quelle fungieren und den Konden­sator in der Gegen­richtung aufladen. Da sich aber die Energie in dem magne­tischen Feld verbraucht, wird dadurch der Konden­sator jetzt mit der entgegen­gesetzten Polarität aufge­laden. Die Spule kommt wieder zur Ruhe, sodass kein Strom mehr fließt. Der Konden­sator beginnt sich erneut zu entladen, jetzt aber in entgegen­gesetzter Richtung.

Dementspre­chend bauen sich in der Spule wieder ein Strom und ein magne­tisches Feld auf. Nach einer gewissen Zeit wird der Konden­sator wieder voll­ständig entladen sein. Die Spule versucht den Strom weiter­hin aufrecht zu erhalten. Und so wird sich der Konden­sator erneut in der ursprüng­lichen Weise aufladen und die Schwingung beginnt von vorne. Wenn es keinerlei Verluste gibt, geht dieses Spiel ständig so weiter.

Grafik (Folie) (wird später eingefügt)

Der Schwing­kreis ist vergleich­bar mit einer „mecha­nischen Schwingung”. Bei einem Feder­oszillator gibt es auch eine maximale poten­tielle Energie. Die schwingende Masse ist ähnlich einem voll­geladenen Konden­sator maximal ausge­lenkt und verharrt in Ruhe. Anschlie­ßend setzt sich die Masse in Bewegung und durch­läuft die Gleich­gewichts­lage. Dort ist die poten­tielle Energie gleich Null.

Die Masse bleibt aber auf­grund ihrer Träg­heit dort nicht stehen, sondern wird jetzt umge­wandelt in kinetische Energie, bis sie auf der Gegen­seite maximal ausge­lenkt ist. Jetzt verharrt die Masse wieder in Ruhe, bis die poten­tielle Energie wieder größer wird. Abschlie­ßend schwingt die Masse erneut in die Ausgangs­lage.

So wie beim Schwing­kreis die Felder zwischen Konden­sator und Spule hin und her schwingen, schwingt auch die Energie beim mecha­nischen Oszillator zwischen poten­tieller und kinetischer Energie hin und her.

Also, das Schwingen des Schwing­kreises entspricht einem Hin- und Herschwingen der Feld­energie zwischen der Energie des elek­trischen Feldes im Konden­sator und der Energie des magne­tischen Feldes in der Spule.

Als Letztes werden wir in diesem Zusammen­hang noch kurz einen „offenen Schwing­kreis” ansprechen.

Grafik (wird später eingefügt)

Hierzu denkt man sich im Schwing­kreis eine Spule, die nur aus einer einzigen Windung besteht.

Bei nur einer Windung kann man den Kreis auch zu einer Geraden strecken, sodass die Platten des Konden­sators jetzt an den Enden einer Geraden liegen.

Grafik (Folie) (wird später eingefügt)

Wenn man nur eine Spule in Form eines einzigen Kreis betrachtet, gibt es nach wie vor das elek­trische Feld zwischen den Konden­sator­platten, und ringförmig um die Strom­leitung einen magne­tischen Feld­wirbel.

öffnet man aber diesen Schwing­kreis zu einer Geraden, hat man keinen klassischen Konden­sator mehr mit eng beieinander­liegen Platten. Jetzt verlaufen die elek­trischen Feld­linien, ähnlich wie bei einer Dipol­anordnung, außen von einer Platte zu anderen herum. Und wenn der Strom in einer solchen geraden Leitung in einer bestimmten Phase zwischen den beiden Platten hin und her läuft, wird es um diesem gerad­linigen Leiter zusätz­lich einen magne­tischen Feld­wirbel geben. Sowohl die Feld­linien als auch der Feld­wirbel sind zeitabhängig.

Und das führt uns im weiteren Verlauf zu den elektro­magnetischen Wellen.

⇦ Kapitel Kapitel ⇨