Tellerfeder berechnen − online

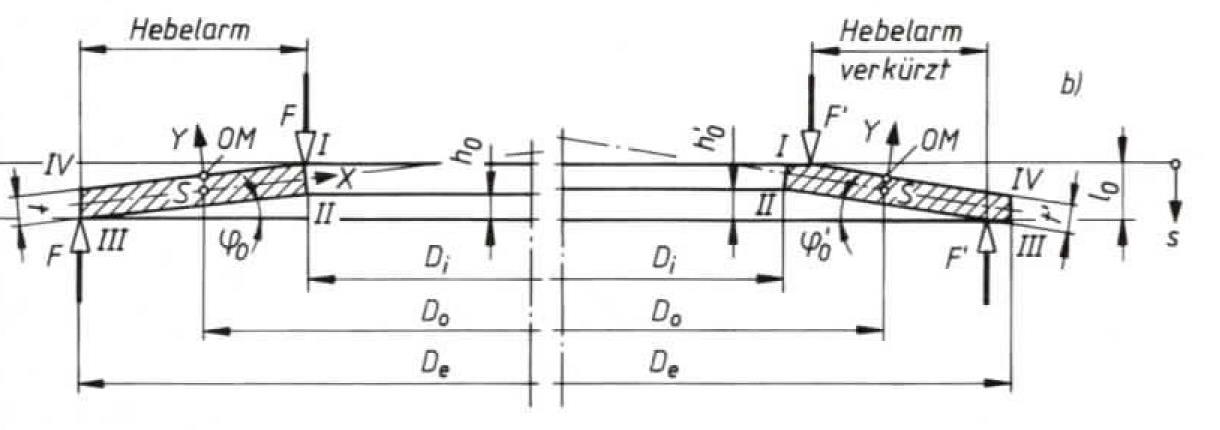
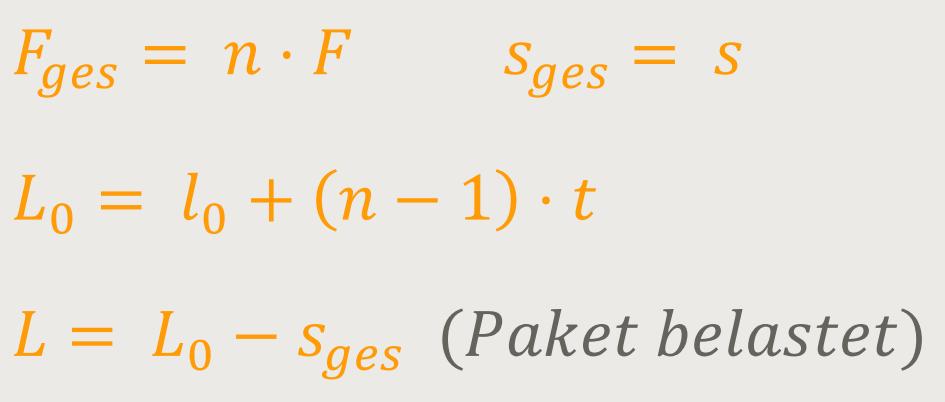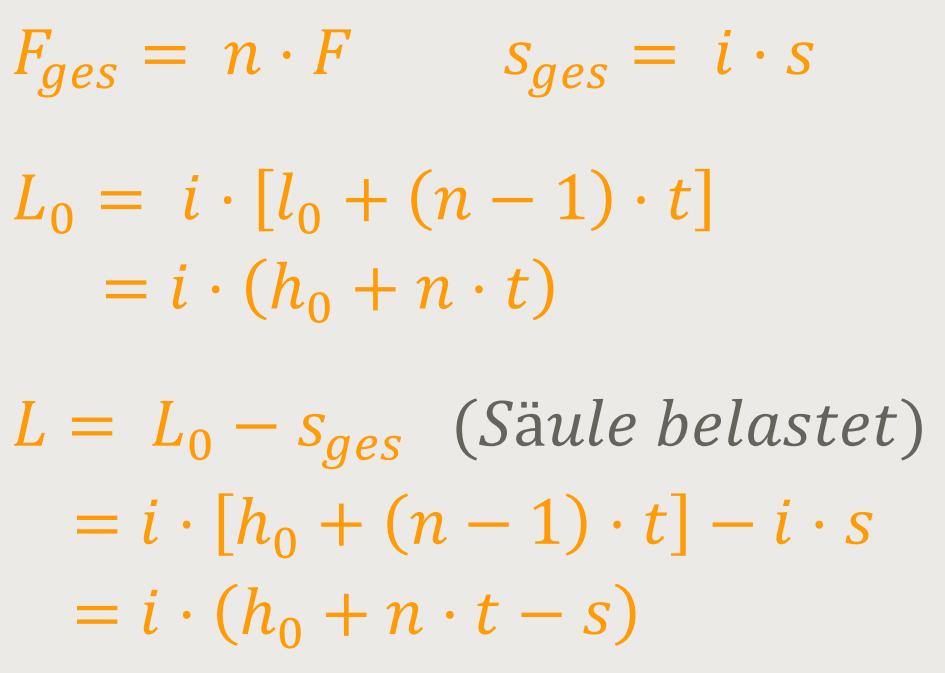Berechnung einer Tellerfeder

⇨ Berechnungstool
⇨ Tellerfedern der Reihe A−C (Tabellen)
⇨ Reibungsfaktor (Tabelle)
⇨ Kennlinienverlauf (Tabelle)

Für den „Einzelteller” werden die zulässigen Federkräfte bei entsprechenden Federwegen in DIN 2093 bzw. vom Hersteller angegeben.

Für ein „Federpaket” aus n gleichsinnig geschichteten Einzelfedern gelten folgende Werte:

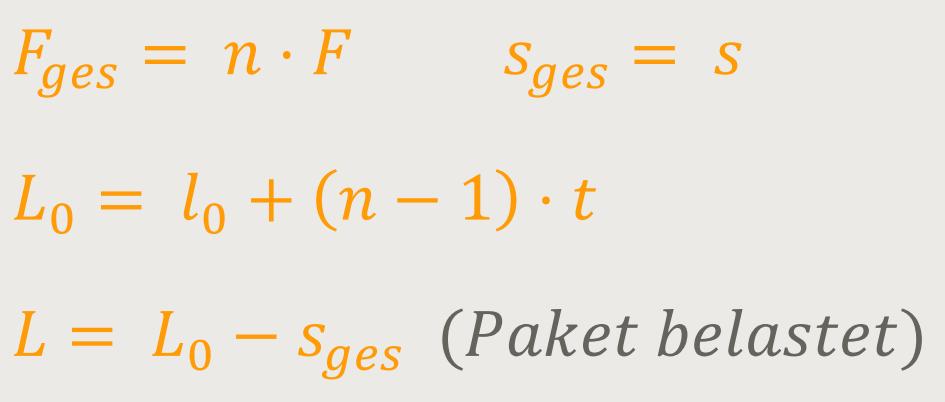
Für eine „Federsäule” aus i wechselsinnig aneinandergereihten Federpaketen aus je n Einzelfedern gelten folgende Werte:

Schritt 1: Parameter festlegen

( Die Vorgabewerte können überschrieben werden )

Wie groß ist die geforderte Federkraft F ?

Wie groß ist der geforderte Gesamtfederweg s ?

Wie groß ist der Feder-Außendurchmesser D_e ?
⇨ siehe Außendurchmesser (Tabelle)

Wie groß ist der Feder-Innendurchmesser D_i ?
(Mindestspiel 0,2 mm bei Dorn/Hülse mit einplanen)
⇨ siehe Innendurchmesser (Tabelle)

Welche Tellerdicke t hat die Feder?
⇨ siehe Tellerdicke (Tabelle)

Welche „reduzierte” Tellerdicke t' hat die Feder?
(nur bei Tellerfedern der Gruppe 3; sonst = 1.0)
⇨ siehe Tellerdicke Gruppe 3 (Tabelle)

Wie groß ist die „innere” Höhe h₀ der gewählten Tellerfeder?
⇨ siehe innere Höhe (Tabelle)

Wie groß ist die Anzahl n der „gleichsinnig” geschichteten Tellerfedern pro Federpaket?

(1 ...)

Wie groß ist der Reibungsfaktor W_M ?
(W_M = Mantelreibung)
⇨ siehe Reibungsfaktor (Tabelle)

(0,003 ... 0,033)

Wie groß ist der Reibungsfaktor W_R ?
(W_R = Randreibung)
⇨ siehe Reibungsfaktor (Tabelle)

(0,012 ... 0,040)

Wie groß ist der Elastizitätsmodul?

N/mm²

... dann ⇨ Schritt 2

Schritt 2: Gesamtkraft F_ges ermitteln

Bei der geforderten Kraft von 2500 N und einer Anzahl von 1 Einzelfedern pro Federpaket muss die Federkraft der Einzelfeder min. betragen: F_ges = 2500.00 N < F_0,75 (Reihe A−C)

Bei Berücksichtigung der Reibung und der geforderten Kraft von 2500 N und einer Anzahl von 1 Einzelfedern pro Federpaket beträgt die zur Verfügung stehende Federkraft: F' = 2425.00 N

Schritt 3: Federkraft in Planlage ermitteln

Die Federkraft in Planlage beträgt: F_c ≈ 3839 N

Schritt 4: Maximale Kraftaufnahme und Kennlinienwert der Feder festlegen

Wie groß ist die maximale Kraftaufnahme F_0,75 (Reihe A−C) der ausgewählten Tellerfeder?
⇨ siehe Reihe A, B oder C − Gruppe 1 ... 3 (Tabellen)

Das Verhältnis der Kräfte F/F_c beträgt (ohne Reibung): 0.65
Daraus ergibt sich ein Verhältnis s/h₀ ≈
(Wert entsprechend der Reihe A, B oder C entnehmen)
⇨ siehe Kennlinienverlauf (Tabelle)

(0,02 ... 1,00)

Das Verhältnis der Kräfte F'/F_c beträgt (mit Reibung): 0.63
Daraus ergibt sich ein Verhältnis s/h₀ ≈
(Wert entsprechend der Reihe A, B oder C entnehmen)
⇨ siehe Kennlinienverlauf (Tabelle)

(0,02 ... 1,00)

Kenndaten

Die Poissonzahl bei Federstahl beträgt: μ ≈ 0,3

Kennwert K₁

Der Kennwert beträgt: K₁ ≈ 0.70

Kennwert K₄

Bei einer Federdicke von 1,5 mm gilt für Tellerfedern der Gruppe 1 und 2 (ohne Auflageflächen):
Der Kennwert beträgt: K₄ = 1

Bei einer reduzierten Federdicke von 1,0 mm gilt für Tellerfedern der Gruppe 3 (mit Auflageflächen):
Der Kennwert beträgt: K₄ = 1.32

Ergebnisse

Schritt 5: Rechnerische Federkraft ermitteln

Die rechnerische Federkraft bei einem Kennwert von K₄ = 1 beträgt: F ≈ 2492 N

Schritt 6: Tatsächliche Federweg s_ges ermitteln

Das Verhältnis der Kräfte...
F/F_c beträgt (ohne Reibung): 0.65 bzw.
F'/F_c beträgt (mit Reibung): 0.63 (s.o.)

Die Anzahl der wechselsinnig aneinandergereihten Federpakete (bzw. Einzelfedern) beträgt: i = 18

Der tatsächliche Gesamtfederweg der Federsäule...
beträgt (ohne Reibung): s_ges = 6.30 mm
beträgt (mit Reibung): s_ges = 6.12 mm

Schritt 7: Länge der Federsäule ermitteln

Die Länge der „unbelasteten” Federsäule beträgt: L₀ ≈ 36.90 mm

Die Länge der „belasteten” Federsäule...
beträgt (ohne Reibung): L ≈ 30.60 mm
beträgt (mit Reibung): L ≈ 30.78 mm

Schritt 8: Die Federrate R ermitteln

Die rechnerische Federrate R = ΔF/Δs nimmt mit zunehmender Einfederung ab.

Die Federrate der gewählten Tellerfeder beträgt: R ≈ 6705 N/mm

Schritt 9: Rechnerische Lastspannungen σ ermitteln

Im Querschnitt der Tellerfeder gibt es keine neutrale Faser, sondern nur einen neutralen Punkt S. Der Stülpmittelkreis ist definiert als D_O = ( D_e − D_i ) / ln δ.

Die Spannung an der oberen Mantelfläche beträgt: σ_OM ≈ -1026 N/mm²

Hinweis: Positive Spannungen sind Zugspannungen, negative Spannungen sind Druckspannungen.

Endergebnis

Bei einer Tellerfeder mit einem Außen−Durchmesser D_e = 25 mm und einer Federdicke von t = 1,5 mm, bestehend aus i = 18 wechselsinnig aneinandergereihten Federpaketen mit jeweils n = 1 Einzelfedern und obigen Kräften beträgt...

die Länge der „unbelasteten” Federsäule: L₀ ≈ 36.90 mm
die Länge der „belasteten” Federsäule: L ≈ 30.60 mm

die max. Federkraft in Planlage: F_c ≈ 3839 N

Hinweis: Die Anzahl der Einzelfedern in einem Federpaket und die sich daraus ergebende Gesamthöhe einer Federsäule sollte so gering wie möglich gehalten werden.

Seitenanfang ⇧

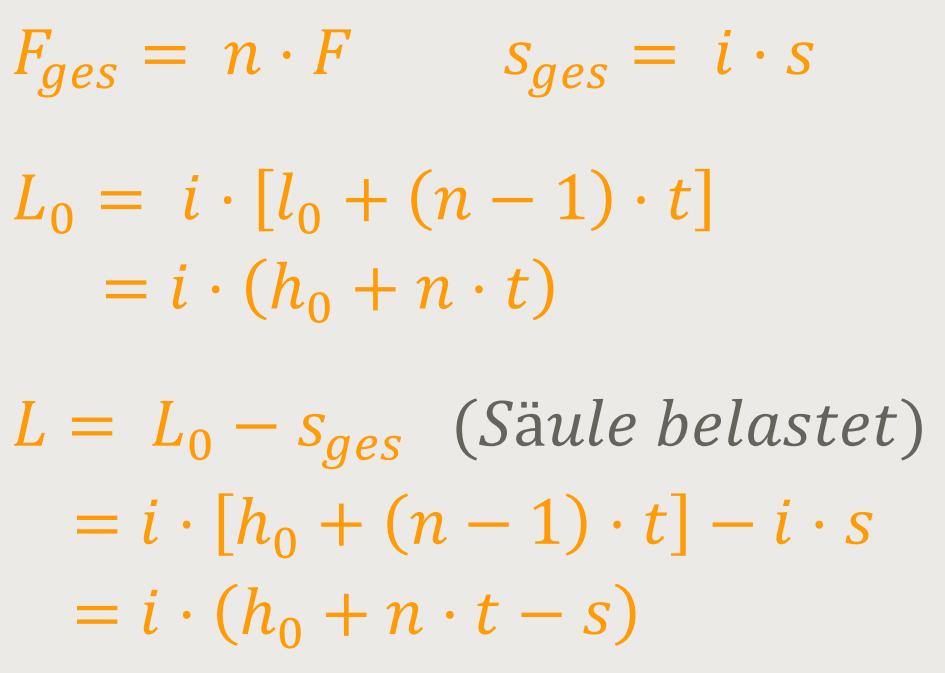
Übersicht − Tabellen

Für Tellerfedern der Reihe A kann eine angenähert gerade Kennlinien angenommen werden.
Für die Reihen B und C ergibt sich ein degressiver Kennlinienverlauf.

⇨ Tellerfedern − Reihe A
⇨ Tellerfedern − Reihe B (0,75 · h₀)
⇨ Tellerfedern − Reihe B (0,5 · h₀) und (0,25 · h₀)
⇨ Tellerfedern − Reihe C (0,75 · h₀)
⇨ Tellerfedern − Reihe C (0,5 · h₀) und (0,25 · h₀)

Tellerfedern Reihe A

D_e /t ≈ 18, h₀ /t ≈ 0,4
Spannung σ_II bei 0,75 · h₀, Spannung σ_OM bei s = h₀,
Kraft in N, Spannung in N/mm²

⇨ Gruppe A1 ⇨ Gruppe A2 ⇨ Gruppe A3

Gr.	D_e h12 mm	D_i H12 mm	Dicke t (t') t (t') + h₀ = l₀	Kraft F_0,75	Span- nung σ_II	Span- nung σ_OM
A1	8	4,2	0,4 + 0,2 = 0,6	210	1218	−1605
A1	10	5,2	0,5 + 0,25 = 0,75	325	1218	−1595
A1	12,5	6,2	0,7 + 0,3 = 1,0	660	1382	−1666
A1	14	7,2	0,8 + 0,3 = 1,1	797	1308	−1551
A1	16	8,2	0,9 + 0,35 = 1,25	1013	1301	−1555
A1	18	9,2	1,0 + 0,4 = 1,4	1254	1295	−1558
A1	20	10,2	1,1 + 0,45 = 1,55	1521	1290	−1560

A2	22,5	11,2	1,25 + 0,5 = 1,75	1929	1296	−1534
A2	25	12,2	1,5 + 0,55 = 2,05	2926	1419	−1562
A2	28	14,2	1,5 + 0,65 = 2,15	2841	1274	−1562
A2	31,5	16,3	1,75 + 0,7 = 2,45	3871	1296	−1570
A2	35,5	18,3	2,0 + 0,8 = 2,8	5187	1332	−1611
A2	40	20,4	2,25 + 0,9 = 3,15	6500	1328	−1595
A2	45	22,4	2,5 + 1,0 = 3,5	7716	1296	−1534
A2	50	25,4	3,0 + 1,1 = 4,1	11976	1418	−1659
A2	56	28,5	3,0 + 1,3 = 4,3	11388	1274	−1565
A2	63	31	3,5 + 1,4 = 4,9	15025	1296	−1524
A2	71	36	4,0 + 1,6 = 5,6	20535	1332	−1594
A2	80	41	5,0 + 1,7 = 6,7	33559	1453	−1679
A2	90	46	5,0 + 2,0 = 7,0	31354	1295	−1558
A2	100	51	6,0 + 2,2 = 8,2	48022	1418	−1663
A2	112	57	6,0 + 2,5 = 8,5	43707	1239	−1505

A3	125	64	8,0 + 2,6 = 10,6	85926	1326	−1708
A3	125	64	(7,5)+ 2,6 = 10,1	85926	1326	−1708
A3	140	72	8,0 + 3,2 = 11,2	85251	1284	−1675
A3	140	72	(7,5)+ 3,2 = 10,7	85251	1284	−1675
A3	160	82	10,0 + 3,5 = 13,5	138331	1338	−1753
A3	160	82	(9,4)+ 3,5 = 12,9	138331	1338	−1753
A3	180	92	10,0 + 4,0 = 14,0	125417	1201	−1576
A3	180	92	(9,4)+ 4,0 = 13,4	125417	1201	−1576
A3	200	102	12,0 + 4,2 = 16,2	183020	1227	−1611
A3	200	102	(11,25)+ 4,2 = 15,45	183020	1227	−1611
A3	225	112	12,0 + 5,0 = 17,0	171016	1137	−1489
A3	225	112	(11,25)+ 5,0 = 16,25	171016	1137	−1489
A3	250	127	14,0 + 5,6 = 19,6	248828	1221	−1596
A3	250	127	(13,1)+ 5,6 = 18,7	248828	1221	−1596

⇨ zum Eingabefeld D_e
⇨ zum Eingabefeld t (t')
⇨ zum Eingabefeld h₀
⇨ zum Eingabefeld F_max

Seitenanfang ⇧

Tellerfedern Reihe B (0,75 · h₀)

D_e /t ≈ 28, h₀ /t ≈ 0,75
Spannung σ_III bei 0,75 · h₀, Spannung σ_OM bei s = h₀,
Kraft in N, Spannung in N/mm²

⇨ Gruppe B1 ⇨ Gruppe B2 ⇨ Gruppe B3

Gr.	D_e h12 mm	D_i H12 mm	Dicke t (t') t (t') + h₀ = l₀	Kraft F_0,75	Span- nung σ_III	Span- nung σ_OM
B1	8	4,2	0,3 + 0,25 = 0,55	118	1312	−1505
B1	10	5,2	0,4 + 0,3 = 0,7	209	1281	−1531
B1	12,5	6,2	0,5 + 0,35 = 0,85	294	1114	−1388
B1	14	7,2	0,5 + 0,4 = 0,9	279	1101	−1293
B1	16	8,2	0,6 + 0,45 = 1,05	410	1109	−1333
B1	18	9,2	0,7 + 0,5 = 1,2	566	1114	−1363
B1	20	10,2	0,8 + 0,55 = 1,35	748	1118	−1386
B1	22,5	11,2	0,8 + 0,65 = 1,45	707	1079	−1276
B1	25	12,2	0,9 + 0,7 = 1,6	862	1023	−1238
B1	28	14,2	1,0 + 0,8 = 1,8	1107	1086	−1282

B2	31,5	16,3	1,25 + 0,9 = 2,15	1913	1187	−1442
B2	35,5	18,3	1,25 + 1,0 = 2,25	1699	1073	−1258
B2	40	20,4	1,5 + 1,15 = 2,65	2622	1136	−1359
B2	45	22,4	1,75 + 1,3 = 3,05	3646	1144	−1396
B2	50	25,4	2,0 + 1,4 = 3,4	4762	1140	−1408
B2	56	28,5	2,0 + 1,6 = 3,6	4438	1092	−1284
B2	63	31	2,5 + 1,75 = 4,25	7189	1088	−1360
B2	71	36	2,5 + 2,0 = 4,5	6725	1055	−1246
B2	80	41	3,0 + 2,3 = 5,3	10518	1142	−1363
B2	90	46	3,5 + 2,5 = 6,0	14161	1114	−1363
b2	100	51	3,5 + 2,8 = 6,3	13070	1049	−1235
B2	112	57	4,0 + 3,2 = 7,2	17752	1090	−1284
B2	125	64	5,0 + 3,5 = 8,5	29908	1149	−1415
B2	140	72	5,0 + 4,0 = 9,0	27920	1101	−1293
B2	160	82	6,0 + 4,5 = 10,5	41008	1109	−1333
B2	180	92	6,0 + 5,1 = 11,1	37502	1035	−1192

B3	200	102	8,0 + 5,6 = 13,6	76378	1254	−1409
B3	200	102	(7,5) + 5,6 = 13,1	76378	1254	−1409
B3	225	112	8,0 + 6,5 = 14,5	70749	1176	−1267
B3	225	112	(7,5) + 6,5 = 14,0	70749	1176	−1267
B3	250	127	10,0 + 7,0 = 17,0	119050	1244	−1406
B3	250	127	(9,4) + 7,0 = 16,4	119050	1244	−1406

⇨ zum Eingabefeld D_e
⇨ zum Eingabefeld t (t')
⇨ zum Eingabefeld h₀
⇨ zum Eingabefeld F_max

Seitenanfang ⇧

Tellerfedern Reihe B (Info-Werte)

D_e /t ≈ 28, h₀ /t ≈ 0,75
Spannung σ_III bei 0,5 · h₀, Spannung σ_III bei 0,25 · h₀,
Spannung σ_OM bei s = h₀,
Kraft in N, Spannung in N/mm²

⇨ Gruppe B1 ⇨ Gruppe B2 ⇨ Gruppe B3

Gr.	D_e h12 mm	Kraft F_0,5	Span- nung σ_0,5	Kraft F_0,25	Span- nung σ_0,25	Span- nung σ_OM
B1	8	89	945	52	505	−1505
B1	10	155	919	88	489	−1531
B1	12,5	215	798	120	423	−1388
B1	14	210	792	120	423	−1293
B1	16	304	796	172	423	−1333
B1	18	417	798	233	424	−1363
B1	20	547	799	304	424	−1386
B1	22,5	533	778	306	415	−1276
B1	25	644	736	367	392	−1238
B1	28	832	781	476	417	−1282

B2	31,5	1410	850	791	452	−1442
B2	35,5	1280	772	731	412	−1258
B2	40	1950	816	1110	435	−1359
B2	45	2700	821	1520	437	−1396
B2	50	3490	816	1950	433	−1408
B2	56	3340	784	1910	418	−1284
B2	63	5270	779	2940	414	−1360
B2	71	5050	759	2890	405	−1246
B2	80	7840	820	4450	437	−1363
B2	90	10400	798	5840	424	−1363
b2	100	9820	749	5620	402	−1235
B2	112	13300	784	7640	418	−1284
B2	125	21900	823	12220	437	−1415
B2	140	21000	792	12000	423	−1293
B2	160	30400	828	17200	445	−1333
B2	180	28600	776	16600	419	−1192

B3	200	58000	892	33400	475	−1409
B3	225	55400	842	32900	450	−1267
B3	250	90200	886	52000	470	−1406

⇨ zum Eingabefeld D_e

Seitenanfang ⇧

Tellerfedern Reihe C

D_e /t ≈ 40, h₀ /t ≈ 1,3
Kraft in N, Spannung in N/mm²

⇨ Gruppe C1 ⇨ Gruppe C2 ⇨ Gruppe C3

Gr.	D_e h12 mm	D_i H12 mm	Dicke t (t') t (t') + h₀ = l₀	Kraft F_0,75	Span- nung σ_III	Span- nung σ_OM
C1	8	4,2	0,2 + 0,25 = 0,45	39	1034	−1003
C1	10	5,2	0,25 + 0,3 = 0,55	58	965	−957
C1	12,5	6,2	0,35 + 0,45 = 0,8	151	1278	−1250
C1	14	7,2	0,35 + 0,45 = 0,8	123	1055	−1018
C1	16	8,2	0,4 + 0,5 = 0,9	154	1009	−988
C1	18	9,2	0,45 + 0,6 = 1,05	214	1106	−1052
C1	20	10,2	0,5 + 0,65 = 1,15	254	1063	−1024
C1	22,5	11,2	0,6 + 0,8 = 1,4	426	1227	−1178
C1	25	12,2	0,7 + 0,9 = 1,6	600	1259	−1238
C1	28	14,2	0,8 + 1,0 = 1,8	801	1304	−1282
C1	31,5	16,3	0,8 + 1,05 = 1,85	687	1130	−1077
C1	35,5	18,3	0,9 + 1,15 = 2,05	832	1078	−1042
C1	40	20,4	1,0 + 1,3 = 2,3	1017	1063	−1024

C2	45	22,4	1,25 + 1,6 = 2,85	1891	1253	−1227
C2	50	25,4	1,25 + 1,6 = 2,85	1550	1035	−1006
C2	56	28,5	1,5 + 1,95 = 3,45	2622	1218	−1174
C2	63	31	1,8 + 2,35 = 4,15	4238	1351	−1315
C2	71	36	2,0 + 2,6 = 4,6	5144	1342	−1295
C2	80	41	2,25 + 2,95 = 5,2	6613	1370	−1311
C2	90	46	2,5 + 3,2 = 5,7	7684	1286	−1246
C2	100	51	2,7 + 3,5 = 6,2	8609	1235	−1191
C2	112	57	3,0 + 3,9 = 6,9	10489	1218	−1174
C2	125	64	3,5 + 4,5 = 8,0	15416	1318	−1273
C2	140	72	3,8 + 4,9 = 8,7	17195	1249	−1203
C2	160	82	4,3 + 5,6 = 9,9	21843	1238	−1189
C2	180	92	4,8 + 6,2 = 11,0	26442	1201	−1159
C2	200	102	5,5 + 7,0 = 12,5	36111	1247	−1213

C3	225	112	6,5 + 7,1 = 13,6	44580	1137	−1119
C3	225	112	(6,2) + 7,1 = 13,3	44580	1137	−1119
C3	250	127	7,0 + 7,8 = 14,8	50466	1116	−1086
C3	250	127	(6,7) + 7,8 = 14,5	50466	1116	−1086

⇨ zum Eingabefeld D_e
⇨ zum Eingabefeld t (t')
⇨ zum Eingabefeld h₀
⇨ zum Eingabefeld F_max

Seitenanfang ⇧

Tellerfedern Reihe C (Info-Werte)

D_e /t ≈ 40, h₀ /t ≈ 1,3
Spannung σ_III bei 0,5 · h₀, Spannung σ_III bei 0,25 · h₀,
Spannung σ_OM bei s = h₀,
Kraft in N, Spannung in N/mm²

⇨ Gruppe C1 ⇨ Gruppe C2 ⇨ Gruppe C3

Gr.	D_e h12 mm	Kraft F_0,5	Span- nung σ_0,5	Kraft F_0,25	Span- nung σ_0,25	Span- nung σ_OM
C1	8	33	759	21	411	−1003
C1	10	48	706	30	383	−957
C1	12,5	130	940	84	511	−1250
C1	14	106	775	68	421	−1018
C1	16	131	740	84	402	−988
C1	18	186	815	121	443	−1052
C1	20	219	782	141	425	−1024
C1	22,5	370	904	240	492	−1178
C1	25	515	926	331	503	−1238
C1	28	681	957	435	519	−1282
C1	31,5	594	831	384	451	−1077
C1	35,5	712	792	548	430	−1042
C1	40	876	782	565	425	−1024

C2	45	1620	922	1040	501	−1227
C2	50	1330	761	854	413	−1006
C2	56	2260	896	1460	487	−1174
C2	63	3660	995	2360	541	−1315
C2	71	4430	987	2860	537	−1295
C2	80	5720	1010	3700	548	−1311
C2	90	6580	945	4230	513	−1246
C2	100	7410	908	4780	493	−1191
C2	112	9040	896	5830	487	−1174
C2	125	13200	968	8510	526	−1273
C2	140	14800	918	9510	499	−1203
C2	160	18800	911	12200	495	−1189
C2	180	22700	883	14600	480	−1159
C2	200	30980	916	19800	498	−1213

C3	225	36300	816	22300	443	−1119
C3	250	41300	805	25600	437	−1086

⇨ zum Eingabefeld D_e

Seitenanfang ⇧

Reibungsfaktor W (Mantel, Rand)

W_M und/oder (W_R)

Schmie- rung	Öl	Fett	Molykote + Öl (1:1)
Reihe A	0,015 ... 0,032	0,012 ... 0,027	0,005 ... 0,022
Reihe A	(0,027 ... 0,040)	(0,024 ... 0,037)	(0,027 ... 0,033)
Reihe B	0,010 ... 0,022	0,008 ... 0,019	0,003 ... 0,015
Reihe B	(0,017 ... 0,026)	(0,016 ... 0,024)	(0,017 ... 0,021)
Reihe C	0,008 ... 0,017	0,007 ... 0,015	0,003 ... 0,012
Reihe C	(0,012 ... 0,018)	(0,011 ... 0,017)	(0,012 ... 0,015)

⇨ zum Eingabefeld W_M
⇨ zum Eingabefeld W_R

Seitenanfang ⇧

Kennlinienverlauf F/F_c

Kennlinienverlauf eines Einzeltellers bei unterschiedlichem Federwegverhältnis s/h₀.

Verhältnis F/F_c	Reihe A s/h₀	Reihe B s/h₀	Reihe C s/h₀
0,05	0,041	0,029	0,020
0,10	0,084	0,060	0,030
0,15	0,128	0,094	0,055
0,20	0,174	0,130	0,075
0,25	0,221	0,168	0,100
0,30	0,270	0,209	0,125
0,35	0,320	0,252	0,150
0,40	0,372	0,298	0,175
0,45	0,425	0,348	0,200
0,50	0,480	0,400	0,225
0,55	0,531	0,449	0,260
0,60	0,582	0,500	0,290
0,65	0,634	0,555	0,325
0,70	0,686	0,611	0,370
0,75	0,739	0,670	0,425
0,80	0,792	0,732	0,480
0,85	0,846	0,795	0,550
0,90	0,900	0,861	0,650
0,95	0,955	0,930	0,750
1,00	1,000	1,000	1,000

⇨ zum Eingabefeld s/h₀

Seitenanfang ⇧

⇦ Kapitel Kapitel ⇨