Man führt also in verschie­denen Prozessen eine Wärme­menge zu. Im ersten Fall hat man das Volumen konstant gehalten. Da war es so, dass nichts von der zuge­führten Wärmemenge in Arbeit umge­wandelt werden kann. Die gesamte Wärme­menge geht in die innere Energie.

Im zweiten Fall hat man den Druck konstant gehalten. Da ist es ein bisschen kompli­zierter. Ein Teil der Wärme­menge geht in die Ände­rung der inneren Energie und ein Teil wird wieder als Arbeits­leistung abge­geben. Damit das System aber immer im Gleich­gewicht bleibt, hat man den Begriff der Enthalpie einge­führt. Auf diese Weise erhält man die Möglich­keit, die zuge­führte Wärme­menge wieder nur als Ände­rung einer einzelnen Zustands­größe dar­zustellen. Und damit kann man diese isobaren Prozesse formal genauso ein­fach beschreiben, wie die anderen beiden.

Im dritten Fall hat man die Temperatur konstant gehalten. Dann geht nichts von der zugeführten Wärmemenge in die innere Energie über. Sondern alles wird in die mechanische Energie umgesetzt.

Was ist aber, wenn das System thermisch isoliert ist? Also, wenn gar keine Wärme­menge zuge­führt oder abge­führt werden kann? So, wie das zum Beispiel bei einer Thermos­flasche der Fall ist. Man kann zwar Arbeit leisten, und es können sich auch der Druck und das Volumen ändern, aber keine Wärme­menge kann über die System­grenzen kommen. Das ist, was man unter einem „adiabatischen” Prozess versteht.

Auch hier legt man wieder den Ersten Hauptsatz (s.o.) zugrunde:

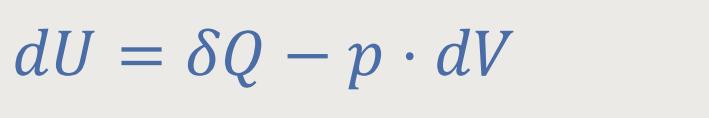
Jetzt ist aber die zuge­führte Wärme­menge δQ = 0. Und damit ergibt sich:

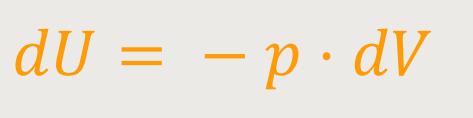
Auch hier orientiert man sich wieder an der Definition der Tempe­ratur (s.o.):

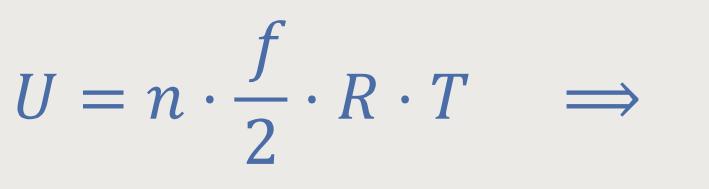
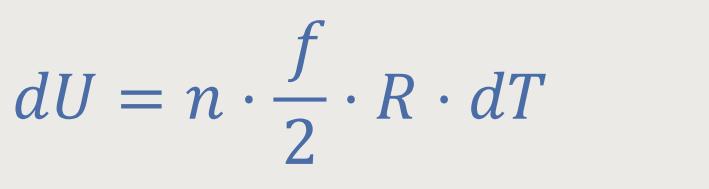
Nach Einsetzen erhält man die Differential­gleichung:

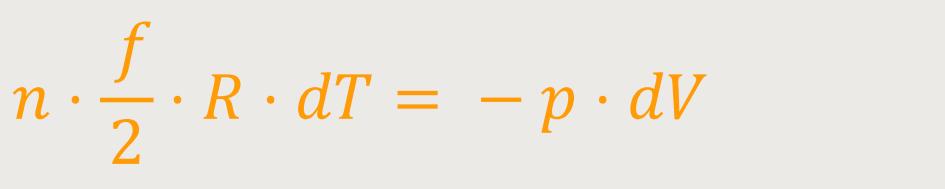
Bevor wir das noch ein bisschen Umformen, greifen wir wieder auf die Zustands­gleichung des idealen Gases zurück:

Wenn man das jetzt entspre­chend in die Differen­tial­gleichung einsetzt, erhält man:

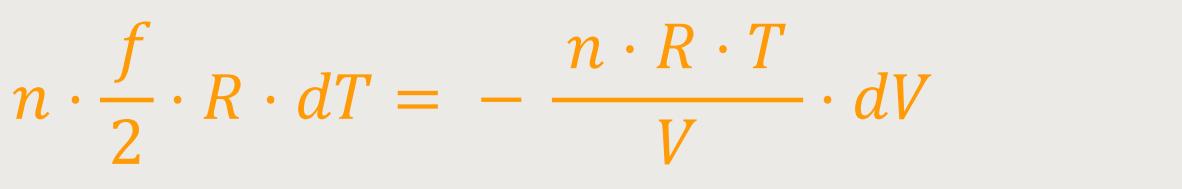
Mathematisch gesehen ist die Thermo­dynamik eine recht ein­fache Ange­legen­heit. Nur mit den Begriffen muss man etwas aufpassen.

Nun lässt sich n noch rauskürzen, wobei (f /2) · R dem C_V, also der Molwärme bei konstantem Volumen, ent­spricht. Und damit bleibt stehen:

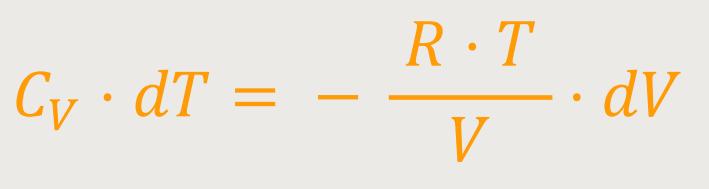
Jetzt kann man noch die Variablen trennen:

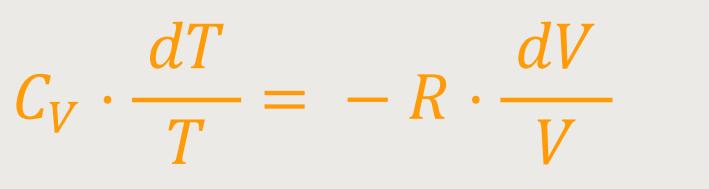
Und wenn man das entspre­chend integriert, ergibt sich daraus:

const   ist eine Integrations­konstante

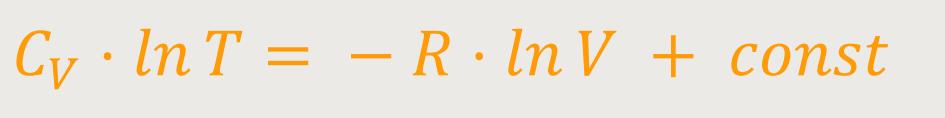
Bei solchen Integra­tionen kann man den Vor­faktor auch in den Expo­nenten schreiben und anschlie­ßend zusammen­fassen:

Das bedeutet wiederum, dass nicht nur für den Logarithmus, sondern auch für die Größe selbst gilt:

Für den Exponenten R kann man auch schreiben:

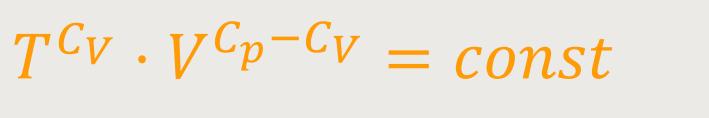
Da κ = C_p/C_V ent­spricht, kann man das noch­mals um­formen:

Und wenn man jetzt die Zustands­gleichung idealer Gase einsetzt, erhält man:

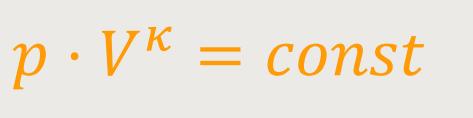
κ (kappa)   ist der Adiabaten-Index (Luft: 1,4)

Also, wenn man ein isothermes System komprimiert, dann geht der Druck hinauf. Aber das System bleibt immer auf der gleichen Tempe­ratur, weil auch Wärme abge­führt wird. Wenn man das System dagegen adiabatisch kompri­miert, und zwar so, dass keine Wärme verloren geht, dann verläuft die Funktion steiler, weil die innere Tempe­ratur ansteigt. Und das bedeutet gleich­zeitig, dass der Druck anwächst. Im p-V-Diagramm werden deshalb die Adiabaten die Isothermen kreuzen.

Bei adiabatischen Tempe­ratur­erhöhungen, sprich bei rascher Kompres­sion, wo die Wärme­menge keine Gelegen­heit hat, schnell zu ent­weichen, wird es heiß und das Gas­gemisch explodiert.

Bevor wir den Zweiten Haupt­satz betrachten, möchten wir eine grund­sätz­liche empirische Erkennt­nis fest­halten. Diese Erkennt­nis ist so offen­kundig, dass sie nicht durch Experi­mente belegt werden muss. Denn nicht alle Vor­gänge, die laut Energie­erhal­tungs­satz erlaubt sind, werden auch wirk­lich ein­treffen. Das ist vor allem dann der Fall, wenn wir von großen thermo­dyna­mischen Systemen aus­gehen, mit denen wir es im All­gemeinen ständig zu tun haben.

In diesem Fall erhebt sich die Frage, inwie­weit gewisse Vor­aus­setzungen, die man über die Bewegung der Moleküle in einem System oder Körper macht, zusätz­liche Ein­schrän­kungen hervor­rufen. Wenn man des Öfteren ein moleku­lares Chaos voraus­setzt, so ist eine solche chaotische Bewegung in der Reali­tät offen­sicht­lich erfüllt.

Diese empirisch gemachten Erfah­rungen kann man in zwei gleich­wertigen Aus­sagen formu­lieren. Die eine Aus­sage stammt von Clausius, die andere von Kelvin. Beide Aus­sagen dienen als Aus­gangs­punkt für unsere weiteren Über­legungen. Wir erhalten damit eine weitere Grund­lage für die Beschrei­bung thermo­dyna­mischer Vor­gänge.

In diesem Zusammen­hang tritt eine weitere empirisch ein­geführte Größe auf, nämlich die „Entropie”. Diese Größe ist genauso unan­schaulich wie die zuvor behandelte Größe der Enthalpie. Die Entropie ist eben­falls eine Zustands­größe, die ein­deutig einem thermo­dyna­mischen Zustand zukommt. Egal auf welchem Weg man diesen Zustand erreicht, lässt sie sich gut berechnen.

Der Zweiter Hauptsatz der Thermodynamik lässt sich auf zweierlei Weise definieren ...

... nach Clausius:

Es gibt „keine” thermo­dyna­mische Zustands­änderung, deren „einzige” Wirkung darin besteht, eine Wärme­menge einem kälteren Wärme­speicher zu ent­ziehen und einem wärmeren zuzuführen.

... nach Kelvin:

Es gibt „keine” thermo­dyna­mische Zustands­änderung, deren „einzige” Wirkung darin besteht, dass einem Wärme­speicher Wärme ent­zogen wird, und voll­ständig in Arbeit umge­setzt wird.

Der­artige Gesetz­mäßig­keiten dürfen nicht außer Acht gelassen werden, weil sie einem Prozess grund­sätz­liche Ein­schrän­kungen auf­erlegen.

Unter einem „Perpetuum mobile zweiter Art” versteht man eine perio­disch arbeitende Maschine, deren einzige Wirkung darin besteht, dass einem Wärme­speicher Wärme ent­zogen wird, und diese dann voll­ständig in mecha­nische Energie um­gesetzt wird. Aus dem Zweiten Haupt­satz ergibt sich entspre­chend:
Es gibt kein solches Perpetuum mobile zweiter Art.

Um die Wichtig­keit und die Bedeu­tung des Zweiten Haupt­satzes klar zu machen, möchten wir noch­mals eine der bereits bespro­chenen Zustands­ände­rungen auf­greifen. Näm­lich eine reversible, isotherme Expansion:

Wir erinnern uns kurz an einen Zylinder mit einem Kolben, in dem sich ein ideales Gas befindet, welches unter einem gewissen Druck steht. Dieser Zylinder befindet sich in einem Wärme­bad, und so wird dem­entspre­chend durch die System­wände Wärme dem System zuge­führt. Das heißt, das System bleibt letzt­lich außen und innen immer auf konstanter Tempe­ratur, und somit in einem Gleich­gewicht. Diesen Prozess nennt man, wie bereits behandelt, eine isotherme Zustands­änderung. Bedingt durch den steigenden Druck im Gas, wird sich der Kolben nach außen bewegen.

Der Erste Hauptsatz besagte ja:

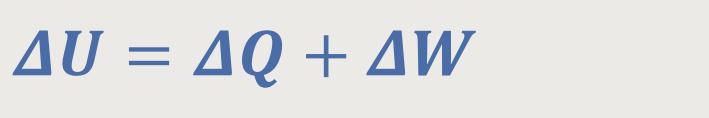
Hiernach kann eine Ände­rung der inneren Energie eines Systems hervor­gerufen werden, indem man ent­weder Wärme­energie zuführt oder mecha­nische Energie zuführt. Ist die jewei­lige Größe mit einem nega­tiven Vor­zeichen ver­sehen, so wird diese ent­spre­chend von dem System abge­führt.

Wenn man aber eine reversible isotherme Expansion des Volumens hat, dann wird ΔU = 0 sein. Denn bei konstanter Tempe­ratur ändert sich die innere Energie in einem idealen Gas nicht. Die Tempe­ratur ist ja ein Maß für die mittlere kinetische Energie eines Moleküls. Und wenn man das entspre­chend mit der Anzahl aller Moleküle multi­pliziert, erhält man die gesamte innere Energie. Da sich die innere Energie nicht ändert, ergibt sich daraus die Schluss­folgerung:

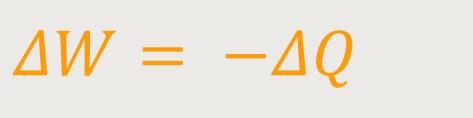
Jetzt hat man genau das, was es laut Zweitem Haupt­satz eigent­lich nicht gibt. Schein­bar wird die zuge­führte Wärme­menge doch voll­ständig in mecha­nische Arbeit umgesetzt.

Oder alternativ könnte man auch schreiben:

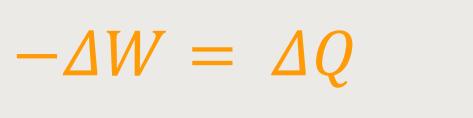
Hiernach ist die vom System abge­führte Arbeit gleich der zuge­führten Wärme­menge.

Der entschei­dende Punkt ist aber, dass das Volumen expan­diert. Man kann hier näm­lich eine zusätz­liche Zustands­änderung beobachten. Und das wider­spricht dem Zweiten Haupt­satz. Natür­lich wäre es schön, wenn man nach einer solchen Über­tragung von Wärme in verrichtete Arbeit, wieder auf den gleichen Zustand zurück­kommt, und sich dieser Schritt dann periodisch wieder­holt. Das wäre ja dann ein Perpetuum mobile zweiter Art: Eine periodisch arbeitende Maschine. Es heißt aber, deren „einzige Wirkung darin besteht ... .” Da wir hier aber eine zusätz­liche Expansion des Systems haben, ist das nicht gegeben.

Also, die reversible isotherme Expansion über­führt die zuge­führte Wärme voll­ständig in die ver­richtete Arbeit. Und das geht immer weiter und weiter. Im Grunde ist das ist ja auch der Sinn von Maschinen, dass sie periodisch arbeiten, und immer wieder die gleiche Zustände durch­laufen werden. Da man immer wieder zum gleichen Ausgangs­zustand zurück­kehrt, hat man es mit einem soge­nannten Kreis­prozess zu tun.

Betrachtet man einen periodischen „Kreis­prozess”, so kann man mecha­nische Energie in Form von Reibung voll­ständig in thermische Energie umsetzen. Dieser Prozess funk­tioniert jedoch nur in eine Richtung, denn man kann gegen­läufig Wärme nicht voll­stän­dig in Arbeit umsetzen.

Es gibt aber verschieden­artige Kreis­prozesse. Und so werden wir zunächst den heraus­greifen, der aus grund­sätz­lichen Über­legungen am ein­fachsten zu beschreiben ist. In Erwei­terung kann man dann anders­artige Kreis­prozesse betrachten, die mehr der Realität entspre­chen. Aber diese lassen wir vor­erst außen vor. Zu Beginn werden wir wieder gewisse Rahmen­bedin­gungen fest­legen, die mög­lichst optimale Inter­preta­tionen zulassen, quasi eine obere Grenze.

Da ist zum Beispiel der soge­nannte Carnot-Kreis­prozess zu nennen. Es geht darum, inwieweit lässt dieser Prozess die Mög­lich­keit zu, Wärme in Arbeit umzu­setzen. Viel­leicht geht es ja doch zu 100%.

Grundlage bildet wieder ein reversibel geführter Kreis­prozess in einem idealen Gas. Reversibel heißt hier, dass man ständig durch lauter Gleich­gewichts­zustände geht. Natür­lich muss man bedenken, dass der Wärme­austausch in der Realität sehr lang­sam abläuft. Aber wir nehmen jetzt einmal an, die Wärme hat Gelegen­heit ständig zuzufließen, sodass die Tempe­ratur im System immer weitest­gehend konstant ist, und man also immer lauter Gleich­gewichts­zustände durch­läuft. Und das würde dann auch mög­lich machen, den Vor­gang umzu­kehren, deshalb der Aus­druck reversibel.

Um sich einen solchen Kreis­prozess vorzu­stellen, betrachtet man ein p-V-Diagramm, in welchem zum Beispiel zwei Isothermen und zwei Adiabaten ein­gezeichnet sind. Da die Funktion der Adiabaten steiler verläuft als die der hyperbel­ähn­lichen Isothermen, kommt es im Diagramm zu vier Kreuzungs­punkten. Verbindet man diese Punkte mit­einander ergibt sich ein Kreis­prozess. Die Eck­punkte kann man vom höchsten aus­gehend, im Uhr­zeiger­sinn mit 1, 2, 3 und 4 bezeichnen. Wir starten bei Punkt 1. Im ersten Schritt bis zum Punkt 2 haben wir eine isotherme Expansion. Es wird bei der höheren Tempe­ratur eine Wärme­menge ΔQ_W dem System zuge­führt. Im zweiten Schritt bis zum Punkt 3 haben wir eine adiabatische Expansion auf eine niedrigere Tempe­ratur. Im dritten Schritt bis zum Punkt 4 haben wir eine isotherme Kompres­sion, indem Arbeit an dem System geleistet wird. Während dessen wird eine Wärme­menge ΔQ_K vom System abge­führt. Und damit steigt die innere Tempe­ratur wieder an. Im vierten und zugleich letzten Schritt zum Ausgangs­punkt 1 haben wir eine adiabatische Kompres­sion. Damit wurde der Kreis­prozess einmal durch­laufen. So stellt man sich einen soge­nannten „Carnot-Kreis­prozess” vor. In der Theorie funk­tioniert so etwas sehr gut, nur die Umsetzung erweist als schwierig, zumindest was den Wirkungs­grad angeht.

Der Carnot-Prozess läuft im Grunde zwischen zwei Wärme­reservoirs ab. Das eine Wärme­reservoir hat die Tempe­ratur T_W (T-warm), und das andere die Tempe­ratur T_K (T-kalt). Wir werden jetzt die Prozesse noch­mals schritt­weise analysieren.

Der Vorteil dieses Carnot-Prozesses besteht darin, dass man nur zwei Arten von Zustands­ände­rungen betrachten muss, näm­lich die isothermen und die adiabatischen. Aber bezogen auf den Kreis­prozess sind es in Summe vier solcher Zustands­ände­rungen. Die Idee ist, dass man für jede dieser Zustands­ände­rungen aus­rechnet, wie groß jeweils die Arbeit ist, die hier ent­weder vom System verrichtet wird oder an dem System geleistet wird. Denn wir wissen ja bereits, wenn man in einem isolierten System eine isotherme Kompres­sion durch­führen möchte, muss von außen Arbeit zuführt werden. Und das Ganze macht nur dann Sinn, wenn netto etwas übrig­bleibt.

Nachdem wir diese vier Schritte nochmals analysiert haben, wird Bilanz gezogen. Das Ergebnis zeigt dann, wie hoch der Wirkungs­grad ist. Zunächst folgt eine kurze Über­sicht von dem, was im Detail betrachtet werden soll.

Es wird beim ersten Schritt Wärme­menge ΔQ_W zuge­führt, damit das System isotherm expan­dieren kann. Anschlie­ßend wird bei allen nach­folgenden Schritten mecha­nische Arbeit geleistet. Im Gegen­zug muss später eine gewisse Wärme das System wieder ver­lassen. Was man aber insbe­sondere wissen möchte ist, was bleibt netto für eine Arbeit übrig, und in welchem Verhältnis steht sie zu der hinein­gesteckten Wärme­menge. Man kann bereits jetzt schon erkennen, dass der Wirkungs­grad nicht bei 100% liegen kann, weil ja etwas von der Wärme­menge wieder raus­geht. Dieser Anteil konnte nicht in Arbeit umge­setzt werden. Und damit ist der erste Haupt­satz der Thermo­dynamik nicht erfüllt und damit auch keine 100% Wirkungsgrad.

Gehen wir die Schritte jetzt nach und nach durch. Wir setzen nach wie vor ein ideales Gas voraus, sowie reversible Zustands­änderungen.

⇦ Kapitel Kapitel ⇨