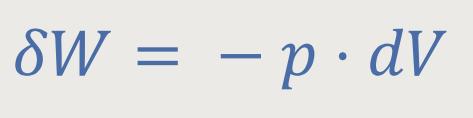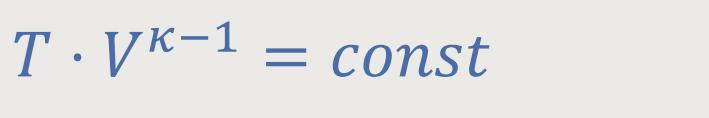Wir haben bereits im vor­herigen Kapitel auf Kreis­prozesse Bezug genommen. Als idealen Modell­prozess, den man zwar in der Praxis nicht so leicht reali­sieren kann, aber dafür umso besser theore­tisch beschreiben kann, ver­wendet man den soge­nannten „Carnot-Kreisprozess”.

Die Betrach­tung von Kreis­prozessen ist insofern sinn­voll, weil jede thermo­dyna­mische Maschine letzten Endes nach dem Prinzip eines Kreis­prozesses läuft. Es werden in perio­dischen Abständen immer wieder die gleichen Vorgänge durch­laufen. Und die Idee ist, dass bei einem solchen Kreis­prozess Wärme zuge­führt wird, die man anschlie­ßend als mecha­nische Arbeit gewinnen kann.

Wir gehen jetzt die bereits ange­sprochenen Schritte nach und nach durch. Wir setzen nach wie vor ein ideales Gas voraus, sowie reversible Zustands­änderungen.

Dieser Schritt ist eine isotherme Expansion.

Wir starten im warmen Wärme­reservoir mit der Tempe­ratur T = T_W.

Ein Wärme­reservoir ist ein System, das groß genug ist, damit es keinen Ein­fluss hat, wenn eine gewisse Wärme­menge ΔQ in einen Kreis­prozess ein­geleitet wird. Beide Wärme­reservoirs sollen weiter­hin nahezu auf der gleichen Tempe­ratur bleiben.

Und weil es ein isothermer Prozess ist, ist das ΔU = 0.

Daher ist auch das ΔQ + Δ W = 0.

Und das bedeutet wiederum:

Wir wissen ja, wenn man ein kleines Volumen ändert, erhält man:

Und wenn man eine nennens­werte Strecke zwischen den Punkten 1 und 2 zurück­legt, muss integriert werden, und daher ergibt sich:

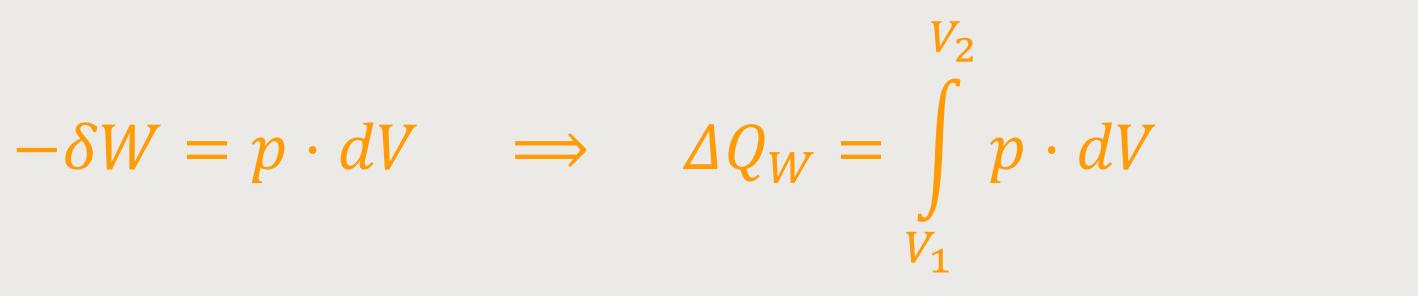
Unter Verwen­dung der Zustands­gleichung idealer Gase erhält man durch Ein­setzen und anschlie­ßendes Umformen:

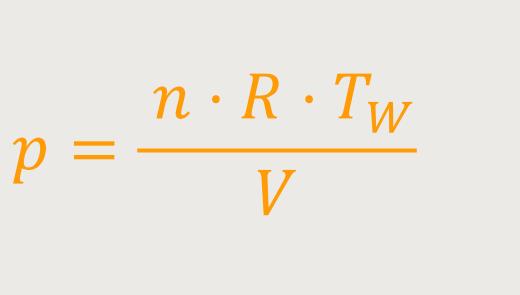
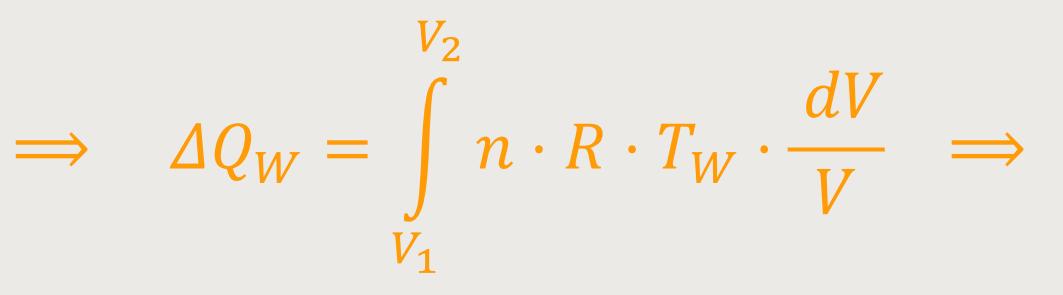
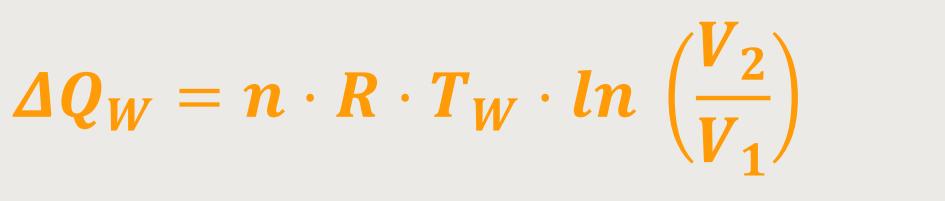
Das heißt, für die Wärme­menge gilt ΔQ_W > 0, und damit wurde dem System eine Wärme­menge zuge­führt. Gleich­zeitig ist die Wärme­menge ΔQ_W = −ΔW und das bedeutet, es wurde auch Arbeit verrichtet und vom System abge­führt.

Dieser Schritt ist eine adiabatische Expansion.

Und weil es ein adiaba­tischer Prozess ist, ist das ΔQ = 0.

Es handelt sich ja um ein thermisch isoliertes System. Und dann verbleibt nur mehr vom Ersten Haupt­satz:

Dadurch erhält man eine Ände­rung der inneren Energie. Und daher ergibt sich für die Arbeit:

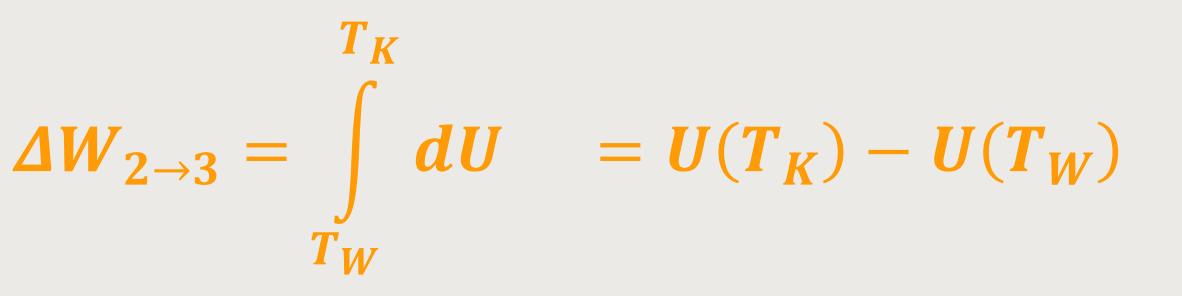
Da die innere Energie propor­tional zur Tempe­ratur ist, wird die Differenz aus U(T_K) − U(T_W) < 0 sein. Somit wird weiter­hin Arbeit von dem System abge­führt. Doch damit ist man bereits an einem Punkt angelangt, von dem an keine Arbeit mehr verrichtet wird. Das belegen die nach­folgenden Schritte.

Dieser Schritt ist eine isotherme Kompression.

Und weil es ein isothermer Prozess ist, ist das ΔU = 0.

Daher ist auch ΔQ + ΔW = 0.

Und das bedeutet wiederum, dass:

Auch hier integriert man wieder entspre­chend obiger Vor­gehens­weise:

Unter Verwen­dung der Zustands­gleichung idealer Gase erhalten man durch Ein­setzen und anschlie­ßen­des Umformen:

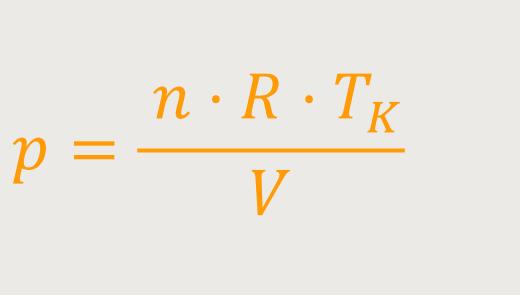
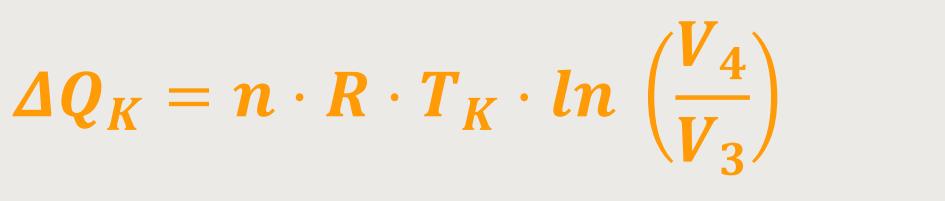
Das heißt, für die Wärme­menge gilt ΔQ_K < 0, und damit wurde vom System eine Wärme­menge wieder abgegeben.

Dieser Schritt ist eine adiabatische Kompression.

Damit kommt man von der kalten Tempe­ratur wieder auf die warme Tempe­ratur.

Und weil es ein adiaba­tischer Prozess ist, ist das ΔQ = 0.

Das bedeutet, wie bereits oben beschrieben:

Und in dem Fall lässt sich das analog zu oben ausrechnen:

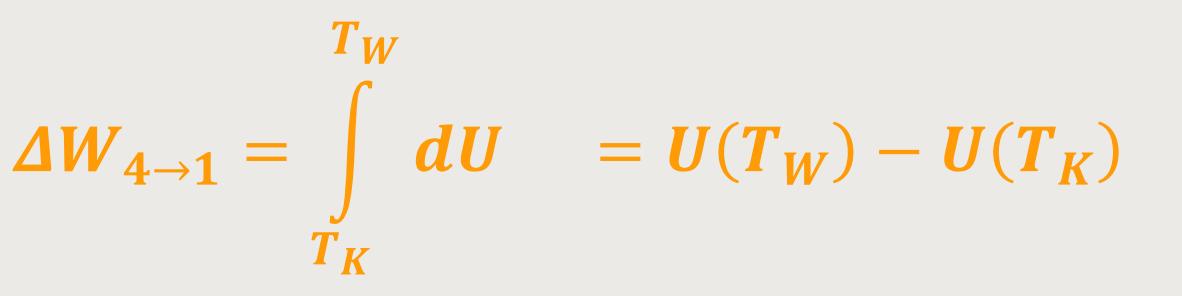
Schauen wir uns an dieser Stelle noch­mals die beiden adiaba­tischen Schritte an. Das heißt, die adiaba­tische Expansion und die adiaba­tische Kompres­sion.

Man erkennt deut­lich, was zunächst als Arbeit vom System geleistet wurde, muss später in gleicher Weise dem System wieder zurück­geführt werden. Diese zwei Schritte sind zwar not­wendig, um von der einen zur anderen Tempe­ratur zu gelangen, und damit auch den Kreis­prozess zu gewähr­leisten. Sie haben aber keinen Ein­fluss auf die geleistete Arbeit.

Letztlich geht es nur um die zwei isothermen Schritte. Hier kann man davon aus­gehen, dass die Bilanz positiver aus­fällt. Also, um die adiabatischen Schritte brauchen wir uns in weiterer Folge nicht mehr zu kümmern. Sie liefern arbeits­mäßig in Summe nichts. Es geht nur mehr darum, die zwei ver­blei­benden isothermen Schritte zu inter­pretieren.

Dennoch ist ein abschlie­ßender Ver­gleich der beiden adiaba­tischen Schritte notwendig. Denn es wäre natür­lich wichtig zu wissen, wie hängt denn V₂ /V₁ mit V₄ /V₃ zusammen?

Wir haben bereits fest­gestellt, dass bei den adiaba­tischen Prozessen die Zustands­ände­rungen wie folgt definiert wurden:

κ (kappa)   ist der Adiabaten-Index

Unter der Voraus­setzung, dass die Zustands­ände­rung längs eines adiaba­tischen Prozesses konstant sein muss, gelten also für die beiden adiaba­tischen Prozesse:

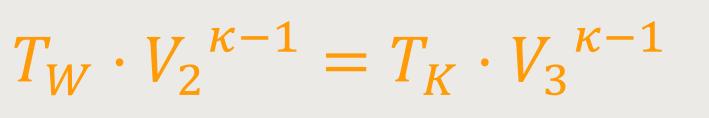
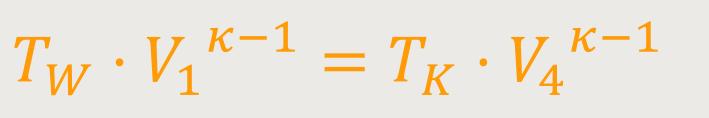
Wenn man beide Bezie­hungen abschlie­ßend mit­einander dividiert erhält man:

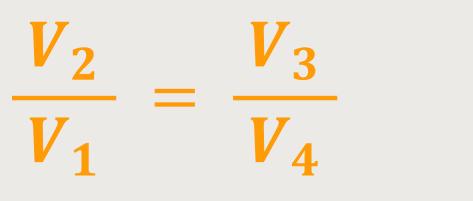
Damit kann man jetzt sofort die entspre­chende Bilanz ermitteln.

Die gesamte geleistete Arbeit stellt sich wie folgt dar:

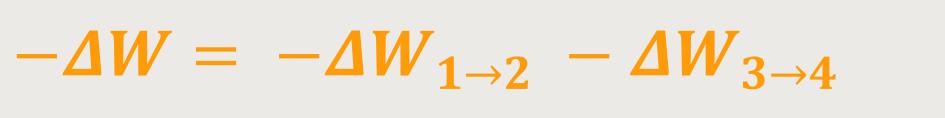
Unter Berück­sichtigung, dass ...

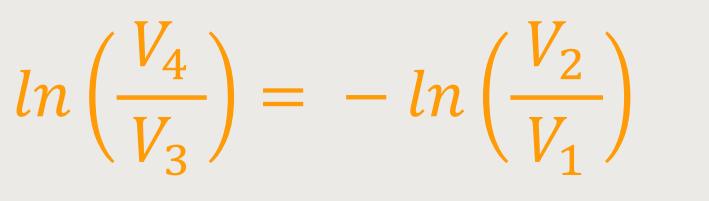
... erhält man entspre­chend durch Einsetzen:

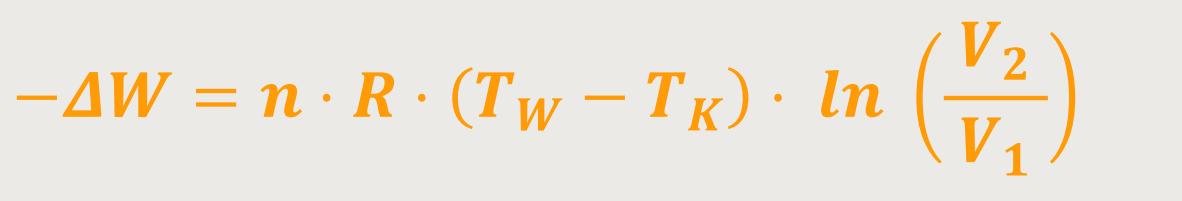
Das heißt, für die Arbeit gilt −ΔW > 0, und damit wird in Summe tatsäch­lich eine Arbeit verrichtet.

Dem gegen­über schauen wir uns noch­mals die Wärme­mengen an:

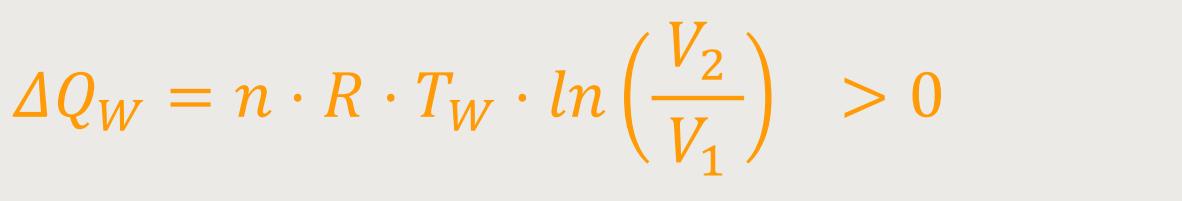
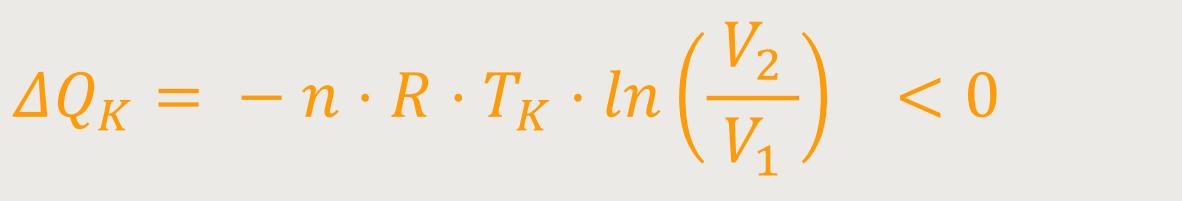
Nachdem wir alle entschei­denden Bilanzen gezogen haben, werden abschlie­ßend die letzten beiden Beziehungen aufsummiert.

Damit erhält man letzten Endes den Zweiten Hauptsatz:

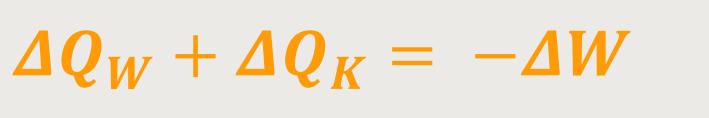
Das, was an Wärme zuge­führt und später als Wärme wieder abge­führt wurde, ergibt das, was letzt­lich an Arbeit geleistet wird. Damit bestätigt sich, dass der Erste Haupt­satz hier erfüllt ist.

Aber noch wichtiger ist der Wirkungs­grad, der in der thermo­dyna­mischen Literatur meistens wie folgt bezeichnet wird:

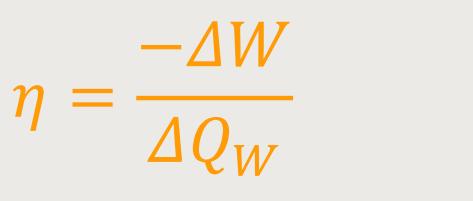
− ΔW   ist die abgeführte Arbeit
ΔQ_W   ist die zugeführte Wärmemenge

Und das ist nichts anderes als die mecha­nische Arbeit, die vom System in Summe verrichtet wurde, dividiert durch die Wärme­menge, die hinein gesteckt werden muss. Leider geht natür­lich auf der anderen Seite eine Wärme­menge ΔQ_K wieder verloren.

Letztlich stellt sich der Wirkungs­grad des Carnot-Prozesses wie folgt dar:

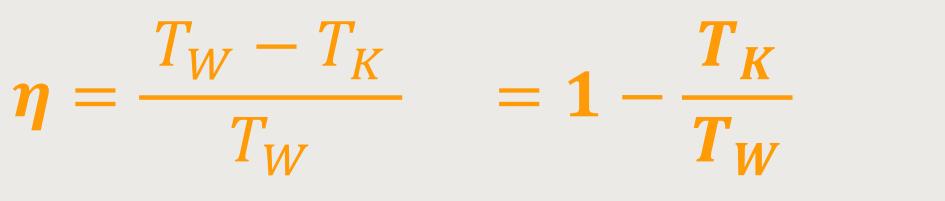
Dementspre­chend hat man einen Wirkungs­grad < 1, der sich danach richtet, wie sich die beiden Tempe­raturen ver­halten. Natür­lich, wenn man einen Wärme­speicher auf den absoluten Null­punkt setzen würde, und bei dieser Tempe­ratur bliebe, dann wäre T_K = 0. Aber das entspräche einer Situation, die gemäß dem Zweiten Haupt­satz nicht möglich ist. In diesem Fall hätten wir einen Wirkungs­grad = 1 , und das geht laut der Kelvinschen Aussage nicht. Außer­dem würde ständig eine Wärme­menge ΔQ_K abgegeben. Und wenn man Kälte abgibt, wird im Umkehr­schluss das System wieder wärmer, wodurch es mit dem absoluten Nullpunkt wieder vorbei wäre. Demnach gilt für den Wirkungs­grad:

Man kann also folgenden Schluss ziehen: Einer­seits ist es zwar in perio­dischen Kreis­prozessen möglich, Arbeit komplett in Wärme über­zuführen, aber es lässt sich nicht Wärme zu 100% in Arbeit um­setzen. Das ergibt sich aus dem Wirkungs­grad < 1. Das haben wir ein­deutig aus der Unter­suchung dieser vier Schritte des Carnot-Kreis­prozesses her­geleitet. Und das ent­spricht auch den Aus­sagen von Clausius und Kelvin.

Wir haben gesehen, dass sehr wohl bei gewissen thermo­dyna­mischen Vor­gängen 100% der hinein­gesteckten Wärme­menge in Arbeit um­gesetzt werden kann. Das funktio­niert zum Beispiel bei einem idealen Gas in einem Zylinder. Wird das System aufgeheizt, dehnt sich das Gas aus und der Kolben bewegt sich. Aller­dings würde dabei nur in eine Richtung Arbeit geleistet, und das macht auf Dauer keinen Sinn. Ziel ist es, nicht nur in eine Richtung eine Bewegung zu erreichen, sondern dass der Kolben auch wieder zurückkommt.

Schließ­lich soll eine perio­disch arbeitende Vor­richtung realisiert werden. Und da gibt es leider die Ein­schrän­kung, dass nicht alles, was man an Wärme­menge hinein­steckt, auch als Arbeit wieder heraus­kommt. Das wäre genau das, was man in Ver­bindung mit den Grund­lagen der Thermo­dyna­mik als Perpetuum mobile der „zweiten” Art bezeichnet. Zur Erinnerung, das Perpetuum mobile der „ersten” Art wäre, man steckt gar keine Energie rein und es arbeitet für einen.

Bei dem der zweiten Art will man zumindest alles, was man hinein­steckt auch wieder als Arbeit heraus­bekommen. Aber selbst das ist nicht mög­lich. Denn einer der Formu­lierungen des Zweiten Hauptsatzes besagt, dass man keine periodisch arbeitende Maschine konstru­ieren kann, die nichts anderes macht, als Wärme­energie voll­ständig in mecha­nische Energie umzu­setzen. Leider wird immer wieder eine gewisse Wärme woanders abge­geben, und geht damit dem System verloren. Um das nachzu­voll­ziehen, betrachtet man obigen Carnot-Prozess.

Eingangs haben wir die einzelnen Schritte dieses Prozesses genau analy­siert und in einem Beispiel durch­gerechnet. Wir haben die zuge­führten und abge­führten Wärme­mengen betrachtet und die Arbeiten, die dabei geleistet werden. Abschlie­ßend werden wir bereits gezogene Bilanz noch etwas beleuchten, um eine weitere Inter­preta­tion heraus­zuarbeiten.

Um ein besseres Verständnis der Abläufe zu erhalten, werden wir den Begriff der „Entropie” ein­führen. Das ist ein Begriff, der erfahrungs­gemäß größere Schwierig­keiten macht. Der Begriff lässt sich nicht so anschau­lich erklären, wie die Kraft, der Druck oder die Tempe­ratur. Mit den meisten physika­lischen Größen können wir etwas anfangen, weil wir sie aus dem Alltag kennen. Obwohl die Entropie eben­falls den All­tag sehr intensiv beherrscht, haben wir keinen unmittel­baren Bezug zu dieser Größe.

Dennoch ist diese Größe auch eine Zustands­größe, die in ihren Eigen­schaften, wie verschie­dene andere auch, objektiv einem Zustand zukommt, egal wie man diesen Zustand erreicht hat. Zustands­größen werden durch den Druck, die Tempe­ratur oder das Volumen charakte­risiert, aber ebenso auch durch die Entropie. Die Wärme war ja, wie wir wissen, keine solche Zustands­größe.

Wie wir weiter oben gesehen haben, beträgt die Bilanz für die gesamte ver­richtete Arbeit während eines Zyklus:

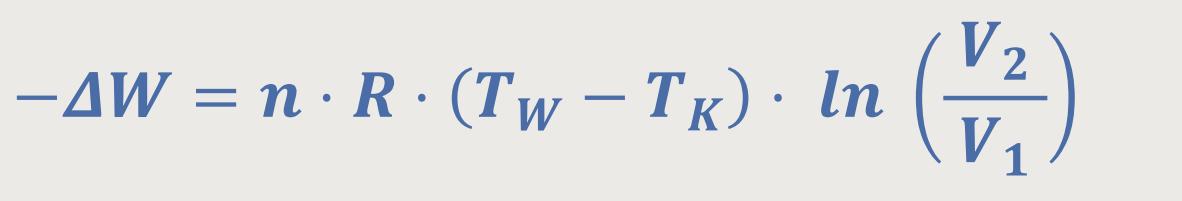
Dieses T_K ist typischer­weise die Tempe­ratur der umge­benden Luft eines Kühl­kreis­laufes. Deshalb hat jedes Auto einen Kühler. Der Kühler ent­spricht dem kalten Wärme­reservoir, an das die Wärme abgegeben wird.

Und das T_W ist die Tempe­ratur, die als Wärme­menge dem System zuge­führt wird. Bei einer Dampf­maschine wäre das die Tempe­ratur des Kessels. Oder beim Verbrennungs-Motor entspricht das der Phase, wo der Treib­stoff zündet.

Die Wärmemengen wurden definiert als:

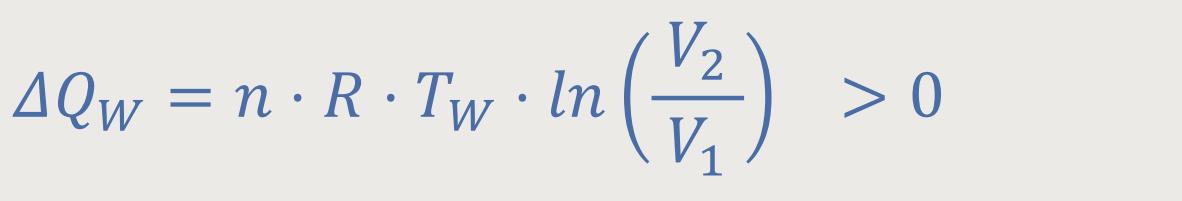
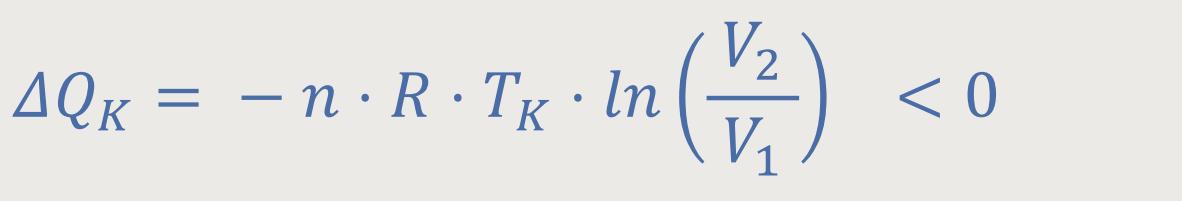
Die erste wichtige Schluss­folgerung, die daraus gezogen wurde, war der Wirkungsgrad:

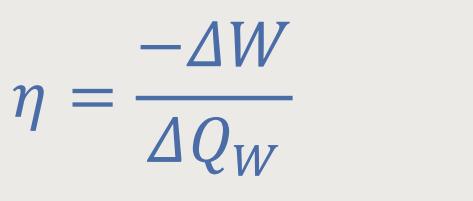
Letztlich erhält man nach Ein­setzten und Wegkürzen den Wirkungs­grad des Carnot-Prozesses:

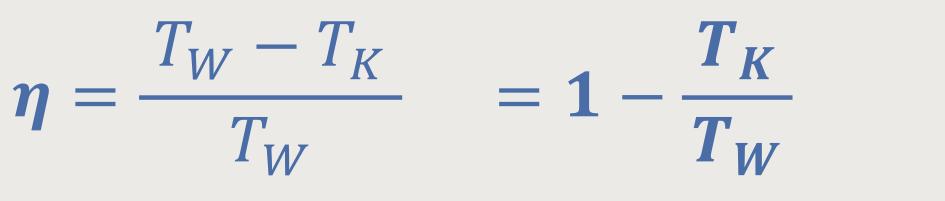
Dieser Wirkungs­grad besagt einer­seits, dass man die zuge­führte Wärme­menge nicht komplett als Arbeit umsetzen kann. Anderer­seits erhebt sich natür­lich die Frage, ob man nicht viel­leicht eine ähn­liche thermo­dyna­mische Maschine reali­sieren kann, die einen besseren Wirkungs­grad hat? Der „Carnot-Satz” besagt aller­dings, dass es keinen höheren Wirkungs­grad gibt. Wie lässt sich das begründen?

Es gibt in der Thermo­dyna­mik bei der­artigen Frage­stellungen oft die Mög­lich­keit, mit einer indirekten Schluss­folgerung vor­zugehen. Um das zu ver­stehen, sind keine speziellen Formeln not­wendig. Hierzu stellt man folgende Über­legungen an:

Bei obigem Carnot-Prozess wurden die einzelnen Schritte im Uhr­zeiger­sinn durch­laufen. Des Weiteren wurde fest­gelegt, dass dies ein rever­sibler Prozess ist. Zusätz­lich läuft der Prozess relativ langsam ab, sodass man in guter Nähe­rung davon aus­gehen kann, dass sich das System zu jedem Zeit­punkt annähernd in einem Gleich­gewichts­zustand befindet. Also könnte man den Prozess auch umdrehen und in Gegen­richtung durch­laufen lassen. Was würde bei diesem Gedanken­spiel mit dem Prozess geschehen?

In diesem Fall müsste man dem System zunächst eine Gesamt­arbeit zuführen. Man könnte quasi sagen, wir kurbeln an dem Carnot-Prozess. Als Ergebnis wird die Wärme dann das System in der Gegen­richtung durch­laufen. Das heißt, es wird dem kälteren Wärme­speicher Wärme ent­nommen und damit dem wärmeren Speicher zusätz­liche Wärme zuge­führt.

Dieses Funktions­prinzip kennt man von der Wärme­pumpe. Das ist im Grunde nur ein gegen­läufiger Kreis­prozess. Und wenn man jetzt wie oben dazu über­geht, das System aufzu­heizen, benötigt man einen sehr großen Wärme­speicher, zum Beispiel aus dem Erdinneren.

Anschließend betreibt man mit einem Elektro­motor eine Wärme­pumpe. Dazu wird natür­lich Arbeit verrichtet, aber die Wärme wird dadurch auch hinauf­gepumpt. Schließlich kann man bei einer höheren Tempe­ratur T_W eine entspre­chende Wärme abgeben. Und das führt dann zu den energie­effizienten Wärme­pumpen, die sich für ein öko­nomisches Heizen immer mehr durch­setzen.

Jetzt könnte man hergehen, und sagen: Nehmen wir an, es gäbe eine Maschine, die einen höheren Wirkungs­grad hat, als der Carnot-Prozess. Dann würde einer­seits die bisherige Carnot-Maschine als Wärme­pumpe zwischen den beiden Wärme­reservoirs ein­gesetzt. Diese Wärme­pumpe wird dann ihrer­seits betrieben von dem anderen Prozess, der einen höheren Wirkungs­grad hat. Was wird dann in Summe passieren, wenn diese beiden quasi wie ein Zwillings­gespann betrieben werden?

In diesem Fall würde die Wärme vom kälteren zum wärmeren Reservoir über­führt werden. Und genau das wider­spricht der Aussage von Clausius. Niemals wird eine Wärme­menge frei­willig und ohne irgend­welche anderen Einflüsse on einem kälteren zu einem wärmeren Reservoir hinüber­wechseln. Und aus dieser logischen Schluss­folgerung heraus, wird es keine Maschine geben, die einen besseren Wirkungs­grad hat, als die Carnot-Maschine.

Daher besagt der Carnot-Satz:

Es gibt keine Maschine, die einen höheren Wirkungsgrad hat.

Hätte man dann näm­lich einen Wirkungs­grad η = 1, und somit ein Perpetuum mobile zweiter Art, würde bei einer zyklisch periodisch arbeitenden Maschine, die zuführte Wärme voll­ständig in mechanische Arbeit umge­setzt werden. Und genau das wurde entspre­chend der Aussage von Kelvin als unmög­lich postuliert. Zudem ergibt sich das auch aus der empirischen Erfahrung. Aufgrund des Energie­satzes wäre das zwar möglich, aber auf­grund des zweiten Haupt­satzes geht das nicht. Und der zweite Haupt­satz gilt insbe­sondere für makro­skopische Systeme.

Man kann also als wesentlichen Punkt festhalten:

Es kann bei periodischen Vor­gängen sehr wohl mecha­nische Arbeit voll­ständig in Wärme umge­setzt werden. Aber umge­kehrt kann Wärme nicht voll­ständig in Arbeit umge­setzt werden. Auf­grund des Wirkungs­grades lässt sich diese Schluss­folgerung ziehen. Das ist ein ganz wesent­licher Umstand in der Thermo­dyna­mik, dass es zwar in der einen Richtung geht, aber in der anderen eben nicht. Wir wollen noch kurz eine andere Fest­stellung betrachten.

Während des Kreis­prozesses wird eine gewisse Wärme­menge ΔQ_W zuge­führt, und im weiteren Verlauf eine andere Wärme­menge −ΔQ_W wieder abge­führt. Wenn man eine Wärme­bilanz durch­führt, erhält man als Ergebnis eine Differenz. Man hat zwar nach einem Zyklus wieder den gleichen Ausgangs­zustand erreicht, mit dem gleichem Druck, der gleichen Temperatur und dem gleichen Volumen. Aber dennoch hat man mehr Wärme hinein­steckt, als man wieder heraus­bekommt.

Daraus lässt sich eben­falls erkennen, dass die Wärme­menge keine Zustands­größe sein kann. Denn wenn sie eine Zustands­größe wäre, müsste diese Wärme­menge dem Ausgangs­punkt objektiv zukommen. Damit gilt für die Wärmemenge nach Durch­laufen eines Zyklus:

Beide Größen kompensieren sich nicht. Denn wenn sich diese beiden ΔQ immer kompensieren würden, könnte der Prozess nie eine Arbeit leisten.

Wenn man diese beiden erarbeiteten Gleichungen ...

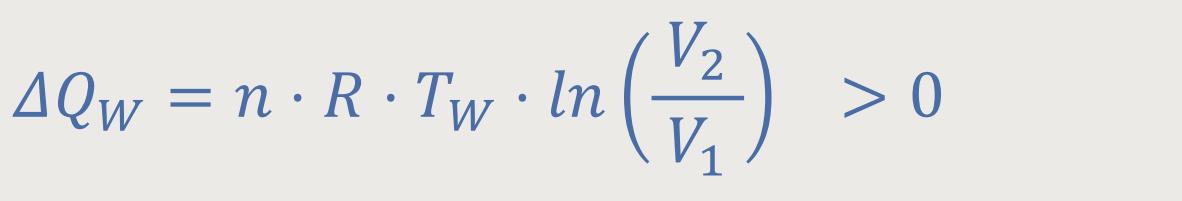
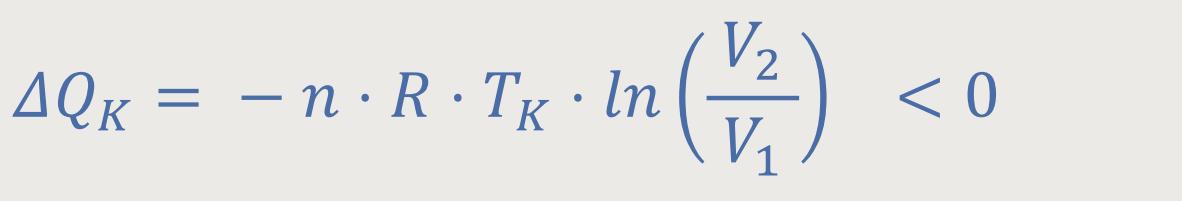
... miteinander addiert, kann man auch etwas Weiteres erkennen:

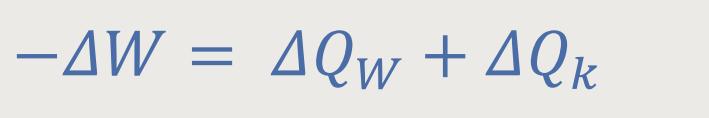
Das entspricht auch dem Energie­erhaltungs­satz und nach Umformung erhält man:

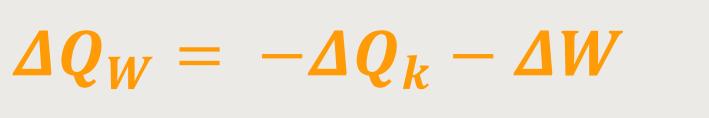
ΔQ_W   ist die zugeführte Wärme
−ΔQ_K   ist die abgeführte Wärme
−ΔW   ist die geleistete Arbeit

Man kann bei der Carnot-Maschine ganz offen­sichtlich einen Wärme­strom erkennen. Da wird etwas vom heißen Reservoir zuge­führt, durch­läuft das System, und anschlie­ßend strömt die Wärme weiter in das kältere Reservoir. Es sind aber nicht die gleichen Beträge, denn es wird immer ein bisschen abgezweigt, und das ist die geleistete Arbeit. Auf diesem Prinzip basieren die Verbrennungs­motoren.

Langsam aber sicher kommen wir auch dem Begriff der Entropie immer näher.

Wir hatten ja aus dem Carnot-Prozess die Folgerungen gezogen:

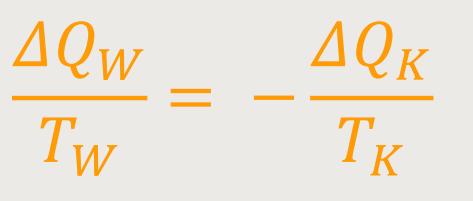
Durch diese Umformung, indem man durch die Tempe­ratur dividiert, kann man die Wärme­mengen quasi auf eine gleiche Größe bringen. So etwas nennt man auch die reduzierten Wärme­mengen.

Oder man kann auch schreiben:

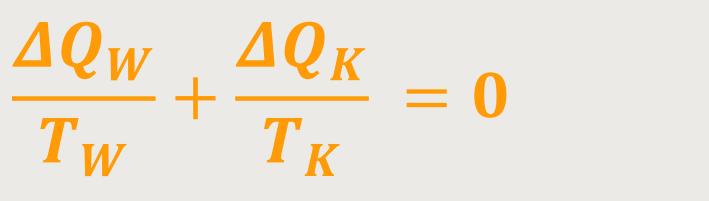
Dadurch erhält man jetzt eine Größe, die sich rund um den ganzen Kreis­prozess wieder kompen­siert. Die Wärme­mengen haben das nicht geschafft, aber mit diesen Größen geht das. Das ist der eigent­liche Gedanke, der dann zur Entropie führt, als einer praktisch verwert­baren Größe, die in dieser ganzen Wärme­problematik wieder als Zustands­größe geeignet ist. Die reduzierten Wärme­mengen können sich nämlich nach einem Zyklus kompen­sieren, sodass wieder Null rauskommt.

Wie sieht es denn bei beliebigen Kreis­prozessen aus? Hier gilt dann ebenso, dass die Summe:

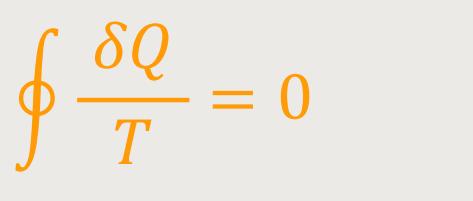
Das ist der berühmte Satz von Clausius.

Und Clausius war es auch, der ursprüng­lich den Begriff der „Entropie” geprägt hat.

Aller­dings gilt das Ganze nur, wenn man reversible Prozesse betrachtet. Und das bedeutet, dass die Summe über einen geschlos­senen Weg im p-V-Diagramm Null ergibt. Das erinnert an die konser­vativen Kräfte, die im Zusammen­hang mit der Mechanik betrachtet wurden. Da war es genauso, dass näm­lich die Arbeit längs eines geschlos­senen Weges Null entspricht.

Jetzt geht es um ein Ring­integral, bei dem es egal ist, längs welcher Richtung man das Integral durch­läuft. Man kommt letzt­lich immer auf den gleichen Wert. Also folgt daraus, dass obiges Integral wegunab­hängig ist. So war es auch bei den konser­vativen Kräften.

Wenn aber dieses Integral wegunab­hängig ist, dann lässt sich wie bei der konser­vativen Kraft vorgehen, indem man ein Potential ein­führt. Bei den Kräften war es die „poten­tielle Energie”. Und was dort die poten­tielle Energie ist, dass ist hier die „Entropie”. Wegen dieser Wegunab­hängig­keit führen wir also ein Potential ein, und definieren uns im nächsten Kapitel die Entropie.

⇦ Kapitel Kapitel ⇨