Bisher haben wir uns mit Systemen beschäf­tigt, in denen ideale Gase eine wesent­liche Rolle gespielt haben. Jetzt sprechen über ein anderes in sich abge­schlos­senes Gebiet, näm­lich die realen Gase. Mittler­weile haben wir sehr oft auf die Zustands­gleichung für ideale Gase Bezug genommen:

Doch in unserer Umwelt haben wir es nur in Ausnahme­fällen mit Systemen zu tun, die sich durch ideale Gase aus­zeichnen. In der Praxis spielen reale Gase eine größere Bedeutung.

Wenn man sich der Reali­tät annähert, hat man eine ganz andere Situation gegen­über der, die wir bei den idealen Gasen kennen­gelernt hatten. Dort hatten wir ja verschie­dene Ideali­sierungen voraus­gesetzt, die in der Praxis nicht 100%ig eintreten können.

Zum einen wurde fest­gelegt, dass die Gas­moleküle nicht mit­einander wechsel­wirken. Wir haben zwar ein Zusammen­stoßen der Moleküle zuge­lassen, aber ansonsten keine Wechsel­wirkung zwischen den Molekülen. Zum andern haben wir voraus­gesetzt, dass die Gas­moleküle ein ver­schwindend kleines Eigen­volumen auf­weisen, also praktisch punkt­förmig sind. Sodass sich in dem ver­füg­baren Volumen nur Punkte bewegen können, ohne selbst ein Volumen ein­zunehmen. Diese beiden Voraus­setzungen werden wir jetzt aufheben.

Wir werden jetzt einer­seits davon ausgehen, dass es zwischen den Molekülen in einem solchen Gas eine gewisse Wechsel­wirkungs­kraft geben wird. Anderer­seits werden wir auch ein gewisses Eigen­volumen der Moleküle mit berück­sichtigen. Die Moleküle sind an sich zwar nicht besonders groß, aber dennoch nehmen sie von dem ganzen Volumen im System einen entspre­chenden Platz ein. Obwohl sich das im ersten Moment relativ harmlos anhört, können trotz­dem deutliche Verände­rungen auftreten.

Es ist natür­lich nicht ganz einfach, das Eigen­volumen und die Wechsel­wirkungs­kräfte quanti­tativ einzu­schätzen. Diese Größen hängen sehr stark von der indivi­duellen chemischen Zusammen­setzung eines Systems ab. Beim idealen Gas hat dies keine wesent­liche Rolle gespielt. Egal, welches Gas man nehmen würde, ob Stick­stoff, Helium oder Argon, es wäre immer die gleiche Beziehung in der Zustands­gleichung. Es bliebe auch immer dieselbe all­gemeine Gas­konstante enthalten.

Wir erinnern uns, das war nichts anderes, als die Avogadro-Zahl multi­pliziert mit der Boltzmann-Konstante. Aber diese Größen haben nichts mit der chemischen Zusammen­setzung zu tun. Nur in dem kleinen n ist in obiger Gleichung etwas ent­halten, und zwar die Molzahl, hinter der aber nichts anderes steckt, als die Anzahl Kilomole der jeweiligen Substanz.

Jetzt müssen wir unseren Blick­winkel etwas ändern. Je mehr man sich der Reali­tät annähert, desto mehr muss man das indivi­duelle Ver­halten verschie­dener Sub­stanzen mit einbe­ziehen. Wenn man nur die beiden vor­genannten Voraus­setzungen ändert, erhalten wir bereits eine leicht verän­derte Zustands­gleichung. Darüber hinaus kommt es zu einem quali­tativ unter­schied­lichen Verhalten der Substanzen. Sehr schnell bewegt man sich im Bereich der Phasen­über­gänge.

Wie zweck­mäßig wäre es doch, wenn man das Molekülvolumen oder die Wechsel­wirkungs­kräfte für die verschie­denen Substanzen aus Grund­größen her­leiten könnte. Das würde vieles ver­einfachen, wenn man die Werte nur in die Gleichungen ein­setzten bräuchte. Aber das wird wahr­scheinlich noch eine geraume Zeit dauern, bis man die Zusammen­hänge besser versteht. Viel­leicht wird uns ein besseres Verstän­dnis der Quanten­mechanik weiter­helfen.

Bis dahin sind wir weiter­hin auf Konstan­ten ange­wiesen, die man wie in so vielen Fällen empirisch ermittelt. Das Messen der verschie­denen Sub­stanzen in Labora­torien führt letzten Endes zu einer großen Anzahl Mess­daten, die man in Tabellen­büchern und mittler­weile im Internet finden kann. Im Grunde kommt es nur darauf an zu wissen, was für Konstanten wir definieren wollen. Eine ähn­liche Frage­stellung hatten wir bereits in Verbindung mit der Elasti­zität von Körpern.

Da gab es zum Beispiel den Dehnungs­modul oder den Kompressions­modul. In der Werk­stoff­technik wünscht man sich auch, dass man sich die Moduln für die verschie­denen Sub­stanzen aus­rechnen kann. Selbst mithilfe der computer­gestützten physika­lischen Berech­nungs­methoden ist die Genauig­keit nicht besonders hoch. Für genauere Ergebnisse, greift man nach wie vor auf der­artige empirische Konstanten zurück. Und so auch hier. Wir werden als erste Voraus­setzung das Molekül­volumen heraus­greifen.

Wenn man von einem end­lichen Molekül­volumen spricht, gibt es in einem System zwangs­läufig Zwischen­räume, die nicht mit Molekülen ange­füllt sind. Auf­grund dessen muss das zur Ver­fügung stehende Volumen um das tat­säch­liche Molekül­volumen reduziert werden, um schließlich das ver­blei­bende Rest­volumen zu ermitteln. Also das Volumen, das wir bisher in der Zustands­gleichung für ideale Gase mit V bezeichnet haben, ist jetzt ein reduziertes Volumen.

Hierfür zieht man einfach das Volumen aller Gas­moleküle in dem System ab. Man sagt auch, es verhält sich propor­tional zur Molzahl und zu einer bestimmten vorge­gebenen Konstante für das entspre­chende Gas.

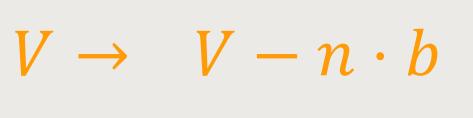
n   ist die Molzahl von Kilomolen
b   ist das Kovolumen (Volumen aller Moleküle pro kmol)

Das gesamte Volumen ist demnach das Volumen aller Moleküle pro kmol multi­pliziert mit der Anzahl der Kilomole in dem betrachteten System. Anschlie­ßend wird das Volumen der Gas­moleküle von dem Behälter­volumen abgezogen. Übrig bleibt dann der freie, für die Bewegung verfügbare Raum.

Im Normal­fall ziehen sich die Moleküle an. Wäre das nicht der Fall, würde vor allem im Falle einer dichteren Anordnung der Moleküle beispiels­weise in einer Flüssig­keit, das Medium nicht zusammen­halten. Bei einem Fest­körper muss es natür­lich eben­falls Wechsel­wirkungen anziehender Art geben, die dem Körper eine feste Form verleihen. Diese Anziehungs­kraft zwischen den Molekülen ist auch in geringem Umfang bei Gasen vorhanden.

Die Wechsel­wirkungs­kräfte haben einen Einfluss auf den Druck in einem System. Der Druck kommt dadurch zustande, dass die Moleküle wie ein Trommel­feuer auf die Gefäß­wände prallen. Solange man von einem idealen Gas spricht, hält sich das Alles im Rahmen. Wenn man hin­gegen ein reales Gas betrachtet, dann liegt eine ähn­liche Situa­tion vor, wie bei der Ober­flächen­spannung in einer Flüssig­keit.

Dadurch, dass die Moleküle mit­einander in Wechsel­wirkung stehen, werden Moleküle, die sich in Wand­nähe befinden, in irgen­deiner Weise von den dahinter­liegenden Nach­bar­molekülen durch deren Anziehungs­kraft zurück­gehalten. Sie prallen mit einem etwas geringeren Impuls auf die Wand. Dadurch wird der Impuls­übertrag kleiner, und das bedeutet einen geringeren Druck. Also muss man sich über­legen, wie groß diese Reduktion des messbaren Druckes an einer Gefäß­wand oder an der Membrane eines Druck­gebers sein wird.

Um der Lösung ein Stück näher zu kommen, kann man zunächst die Anziehungs­kraft nur eines Moleküls betrachten. Also ein Molekül, das sich bereits in Wand­nähe befindet, und unmittel­bar dagegen prallen wird. Dadurch wird ein Impuls­über­trag bewirkt, der dann letzt­lich den Druck hervor­ruft, der auf diese Wand ausge­übt wird.

Diese Anziehungs­kraft verhindert, dass ein wand­nahes Molekül mit voller Wucht gegen die Wand prallt. Jetzt hat man aber nicht nur ein einzelnes Molekül, das für den Druck verant­wort­lich ist, sondern es wird eine große Anzahl von Molekülen pro Zeit­einheit auf die Behälter­wand treffen. Diese Anzahl ist natür­lich auch wieder propor­tional zu der Molekül­anzahl­dichte in dem Gas. Je größer die Anzahl pro Volumen­einheit, desto mehr treffen auf die Wand.

Dadurch ergibt sich, dass der Druck, der gemessen wird, kleiner ist als der Druck, der eigent­lich im Innern des Systems vor­handen ist. Denn gemessen wird immer nur an einer Wand bzw. einer Membrane. Aber im Inneren des Gases, wo sich die Gas­moleküle frei bewegen können, und von anderen Molekülen umgeben sind, fällt die ein­seitige Kraft­wirkung weg. Wenn der Druck im Innern also größer wird, ergibt sich für den Druck

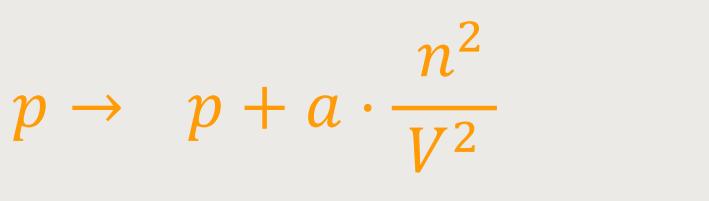
a   ist ein Proportionalitätsfaktor
a · n²/V²   nennt man den Binnendruck

Also, das Volumen, das wirklich für die Bewegung der Moleküle zur Verfügung steht, ist kleiner als das Volumen des Gefäßes. Und der Druck, den die Moleküle im Inneren ausüben, ist größer als der Druck, den man durch irgen­deinen Sensor misst.

Mit diesen beiden Erweite­rungen für p und V lässt sich jetzt die ein­gangs erwähnte Zustands­gleichung in eine praxis­nahe Form bringen. Als Basis dient weiter­hin die verein­fachte Zustands­gleichung für ideale Gase, aber jetzt ergänzen wir entspre­chend, indem wir einsetzen:

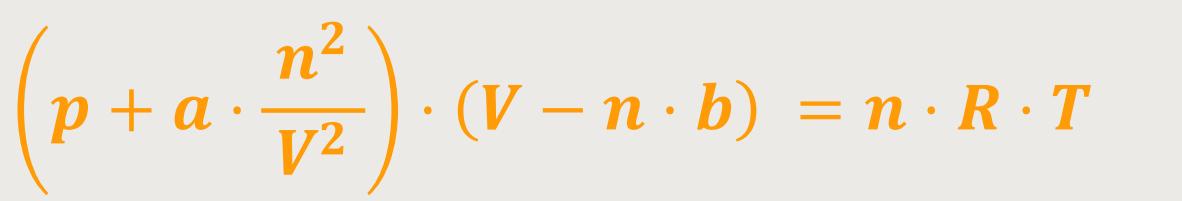
Das ist die Van-der-Waalssche Zustands­gleichung.

Diese Gleichung sieht ohne Frage anders aus, als die bisher verwen­dete, und sie lässt auch auf einen anderen Zusammen­hang zwischen p, V und T schließen. Aller­dings es ist nicht die einzige Zustands­gleichung, mit der man das Ver­halten von Gasen mög­lichst realis­tisch beschreiben kann. Man wird in der Literatur noch auf viele weitere Varianten stoßen.

Mittels eines p-V-Diagramms lässt sich diese Gleichung für gewisse realis­tische Parameter aus­rechnen. Die Isothermen werden bei der Dar­stellung eines Gases auf Grund­lage der Van-der-Waals-Gleichung etwas anders aussehen. Beim idealen Gas gleichen die Isothermen Hyperbeln. Wir erinnern uns, für Isothermen gilt, dass die Tempe­ratur T = const ist, woraus folgt, dass auch p · V = const ist.

Bei den Van-der-Waals-Gasen wird p · V ≠ const sein. Als Ergebnis erhält man keine klassischen Hyperbel­äste mehr, sondern jetzt zeigen die Kurven­ver­läufe wellen­förmige Aus­buch­tungen, die bei immer niedri­geren Tempe­raturen nach unten immer größer aus­fallen.

Grafik (wird später eingefügt)

Wenn man sich im Bereich von hohen Tempe­raturen (z.B. 1000 K) befindet, ver­laufen die Isothermen nahezu hyper­bolisch. Je mehr die Tempe­ratur aller­dings abnimmt, erhält diese Kurve Richtung Koordinaten-Ursprung eine Wölbung. Und diese Wöl­bung wird immer stärker, je niedriger die Tempe­ratur wird. Schließ­lich kommt einmal der Punkt, wo sogar eine waage­rechte Tangente auftritt. Wenn man mit der Tempe­ratur noch weiter hinunter­geht, ergibt sich sogar ein wellen­förmiges Minimum, mit einer starken Aus­buchtung. Welche Rück­schlüsse kann man daraus ziehen?

Laut p-V-Diagramm erreicht der Druck ein Minimum, und steigt bei einer Erhöhung des Volumens wieder an. Das wirkt auf den ersten Blick merk­würdig, und man würde das als nicht physika­lisch ansehen. Denn als Betrachter geht man immer noch von einem end­lichen Molekül­volumen mit seinen Wechsel­wirkungs­kräften aus. Alles unter Berücksichtigung eines ein­heit­lichen homogenen Systems. Das macht auch Sinn, denn sonst könnte man die Gas­gleichung nicht einsetzten.

Trotzdem können ab einem bestimmten Bereich Merk­wür­dig­keiten auf­treten, die nicht hyperbel­ähnlich ver­laufen. Bei der Unter­suchung realer Systeme liegt das daran, dass in dem abwei­chenden Bereich offen­sichtlich ein Phasen­über­gang statt­findet. In einem p-V-Diagramm gibt es nämlich einen gewissen Bereich, in welchem Phasen­über­gänge ablaufen. Oberhalb dieses Bereiches ver­laufen die Isothermen noch nahezu hyperbelähnlich.

Je geringer aber die Tempe­raturen werden, desto mehr verändert sich der Verlauf der Isothermen. Jede weitere Isotherme, die diesen Bereich schneidet, verläuft dann waage­recht weiter und wenn sie aus dem Bereich wieder aus­tritt, setzt sie den hyperbel­ähn­lichen Ver­lauf fort. Wie lässt sich das inter­pretieren?

Das System wechselt von einem homogenen in ein inhomogenes System über. In dem Bereich, wo die Kurven quasi eine nicht physika­lische Welle zeigen, spricht man von einem Bereich der Zwei­phasigkeit. Je nach Tempe­ratur, wechselt das System bei einem gewissen Druck, von dem einen in das andere System. Ober­halb hin­gegen bleibt es bei dem homogenen ein­phasigen Bereich. Der entschei­dende Punkt ist hierbei, dass während dieser Zwei­phasig­keit eine gas­förmige Phase und eine flüssige Phase neben­einander koexistieren. Was heißt das im Detail?

Nehmen wir an, wir hätten ein großes Volumen und entspre­chend einen kleinen Druck. Jetzt verringern wir das Volumen des Gases, indem wir zum Beispiel Wasser­dampf kompri­mieren. Darauf­hin wird der tatsäch­liche Druck dieses Dampfes in dem System ansteigen. Irgend­wann kommt der Punkt, wo das nicht mehr ohne weiteres fort­gesetzt werden kann. Die Moleküle lassen sich nicht mehr weiter kompri­mieren. Demzu­folge beginnt jetzt ein Phasen­über­gang von dem gas­förmigen Wasser­dampf zum flüssigen Wasser.

Man kann sagen, sobald es irgend­welche Stör­stellen gibt, beispiels­weise Ionen, beginnt die Bildung der neuen Phase. Meistens geschieht das mithilfe von irgend­welchen kleinen Molekül-Clustern, die sich plötz­lich zusammen­fügen, und die dann Ausgangs­punkt für die Formierung der neuen Phase sind. Diese Keim­bildung oder „Nukleation” voll­zieht sich sehr schnell, und ist der erste Teil­prozess, der einen Phasen­über­gang erster Ordnung einleitet.

Doch wenn man das System weiter kompri­miert, wird der Druck nicht mehr ansteigen. Viel­mehr bleibt der Druck eine Zeit lang konstant. Man spricht hier auch von einem soge­nannten Sätti­gungs­druck. Je kleiner die Tempe­ratur ist, desto kleiner ist auch der Sätti­gungs­druck. Während das System diese Gleich­gewichts­zustände durch­läuft, wird von dem Gas immer mehr in Flüssig­keit über­gehen, und der Dampf wird weiter abnehmen.

Während dieses Prozesses teilt sich der durch­schrittene Bereich in zwei Teil­abschnitte auf. Ein Teil ist bereits ver­flüssigt, wogegen der andere Teil noch dampf­förmig ist. Ab einem bestimmten Punkt ist der gesamte Dampf in Flüssig­keit über­gegangen. Es gilt zu berück­sichtigen, dass sich weder die Anzahl der Moleküle, noch die Tempe­ratur geändert haben. Und auch der Druck ist konstant geblieben, wenn­gleich es sich hierbei um den Sätti­gungs­druck der Flüssig­keit in dem System handelt.

Hierzu kann man sich einen senk­recht stehenden Zylinder mit einem Kolben vor­stellen. Die untere Hälfte des Volumens ent­hält Flüssig­keit, wogegen die obere Hälfte mit Wasser­dampf gefüllt ist. Das System hat zudem eine bestimmte Tempe­ratur. Wenn man das Volumen des Dampfes ändert, wird sich der Druck nicht ändern. Das System kann nicht mehr als diesen Sätti­gungs­dampf­druck her­stellen. Selbst wenn man mit einem Kolben den Dampf weiter kompri­miert, werden etliche Moleküle in den flüssigen Zustand hinein­konden­sieren. Aber der Druck wird dadurch nicht steigen.

Man könnte hier von einer maximalen Spann­kraft sprechen, die diese Flüssig­keit gegen den Dampf hat. Es herrscht quasi bei einer bestimmten Tempe­ratur ein Gleich­gewichts­zustand zwischen Flüssig­keit und Dampf. Das Ganze funk­tioniert solange, bis nur noch Flüssig­keit vor­handen ist, und man schließ­lich mit dem Kolben an der Flüssig­keits­ober­fläche anstößt. An dieser Stelle lässt sich das System nur noch mit sehr hohem Aufwand kompri­mieren, weshalb der Druck auch steil ansteigen wird. Je niedriger die Tempe­ratur ist, desto steiler steigt der Druck an.

Im Bereich des Zwei­phasen­gebietes gibt es eine Koexistenz von flüssiger und gas­förmiger Phase. Diese zwei Koexistenzen werden im Van-der-Waals-Diagramm durch eine Wellen­linie dar­gestellt. Vom Anfangs­punkt bis zum End­punkt ver­läuft eine waage­rechte Schnitt­linie. Diese Grenz­linie ent­spricht dem bestimmten Sätti­gungs­druck bei einer bestimmten Tempe­ratur. Durch die Wellen­linie entsteht einer­seits ein Wellen­tal mit einer Teil­fläche A und anderer­seits ein Wellen­berg mit einer Teilf­läche B. Beide Teil­flächen stehen für die zwei Phasen, und sind jeweils gleich groß.

Die Van-der-Waals-Gleichung liefert nur die Wölbung bestehend aus dem Minimum und Maximum. Wenn man die tatsäch­liche Gleich­gewichts­dampf­linie sucht, so ist das die Waage­rechte, bei der die beiden Teil­flächen gleich groß sind. Jetzt hat diese Dar­stellung aber auch noch eine dritte Dimension, näm­lich die Tempe­ratur. Und so lässt das auch 3-dimen­sional darstellen.

Hierzu nimmt man wieder das p-V-Diagramm als Grund­lage, und trägt zusätz­lich im Diagramm die Tempe­ratur als T-Achse in z-Rich­tung ein. Für eine bestimmte Tempe­ratur T ergibt sich zunächst eine hyperbel­ähnliche Zunahme. Dann wird das Phasen­gleich­gewicht zwischen flüssig und gas­förmig durch­schritten. Und schließlich hat man den steilen Weiter­verlauf in der flüssigen Phase. Je weiter die Tempe­ratur zurück­geht, wird irgend­wann noch ein Phasen­über­gang zum festen Körper ein­treten, dessen Kurve noch­mals steiler ansteigt. Diese dritte Phase lässt sich dann nur noch sehr schwer kompri­mieren, weshalb es zu sehr großen Druck­zunahmen kommt.

Wenn man die Tempe­ratur als dritte Achse in ein 3-dimen­sionales p-V-T-Diagramm auft­rägt, erhält man im flüssig/gas­förmigen Bereich eine räum­liche Fläche, die relativ moderat ansteigt. Wenn die Temperatur zunimmt, ergeben sich die verschie­denen Isothermen, bis zum End­punkt der Fläche, wo die Isotherme nur noch eine Flach­stelle aufweist. Dieser Punkt wird als kritischer Punkt bezeichnet, doch dazu später mehr.

Es bietet sich auch die Mög­lich­keit, das 3D-Diagramm in P-T-Aus­richtung zu betrachten. In diesem Fall zeigt die V-Achse nach vorne. Jetzt sieht die Sache ganz anders aus. In einem P-T-Diagramm hat man zunächst eben­falls einen Anstieg des flüssig/gas­förmigen Bereiches. Und auch hier verläuft die Grafik in einer 2-dimen­sionalen Linie bis hinauf zu dem kritischen Punkt. Die flache Kurve beschreibt die Phasen zwischen gas­förmig und flüssig.

Aber dann gibt es noch eine zweite stark ansteigende Fläche, die sich bildet, wenn der Über­gang zwischen flüssig und fest statt­findet. Diese Linie, von der alle Flächen weg­laufen nennt man „Tripel­linie”, weil hier die Zustände gas­förmig, flüssig und fest in Koexistenz sind. Und wenn man sich die Linien­verläufe anschaut, stoßen alle am Tripel­punkt zusammen.

Die Linie vom Tripel­punkt TP zum kritischen Punkt C beschreibt den Sätti­gungs­druck P_s bei einer bestimmten Tempe­ratur T. Für jede Tempe­ratur erhält man einen entspre­chenden Sätti­gungs­druck. Das kann man in der Grafik direkt ablesen. Die erste Linie, die den Sätti­gungs­druck beschreibt, teilt den gas­förmigen vom flüssigen Bereich ab. Die zweite, steiler ver­laufende Linie, trennt den flüssigen vom festen Bereich ab. Die Linien sind soge­nannte Koexistenz-Linien. Und so erhält man ein sehr über­sicht­liches Phasen­diagramm in der Druck-Temperatur Auf­tragung zwischen dem gas­förmigen Bereich, dem flüssigen Bereich und dem festen Bereich.

Bei niedrigen Tempe­raturen und hohen Drücken ist das System fest. Bei höheren Tempe­raturen wird das System flüssig. Und wenn die Drücke kleiner werden, bildet sich im System Dampf. So laufen die Phasen im Wesent­lichen ab.

Wasser (H₂O) zeigt in einem solchen Phasen­diagramm eine gewisse Anomali­tät. Wenn man die Koexistenz-Linie zwischen flüssig und fest betrachtet, kann man erkennen, dass bei zuneh­mendem Druck die Tempe­ratur sogar zurück­geht. Wenn man zum Beispiel Eis einem starken Druck aus­setzt, dann schmilzt es, was bei Kohlen­dioxid nicht der Fall ist. Wasser hat somit eine Anomalie, die für uns lebens­wichtig ist.

Bei 4 °C erreicht man bei Wasser den Punkt höchster Dichte. Wenn man die Tempe­ratur unter 4 °C senkt, wird die Dichte des flüssigen Wassers wieder geringer. Eis hat eine entspre­chend geringere Dichte, sonst würden keine Eis­schollen auf dem Wasser schwimmen. Diese so schein­bar unwichtige Anomalie bildet für uns eine wesent­liche Existenz­grund­lage. Wäre das nicht so, würde alles Eis im Meer sofort zu Boden sinken. Dann wäre das Meer längst vom Meeres­grund her zuge­froren. Die mole­kulare Eis­struktur ist demnach lockerer als die moleku­lare Wasser­struktur. Oder anders ausge­drückt, gefrorenes Wasser nimmt ein höheres Volumen ein, als flüssiges Wasser bei gleicher Molekülanzahl.

Je nach Material gibt es bei einem bestimmten Druck mit einer bestimmten Tempe­ratur einen kritischen Punkt. Unter­halb dieses Punktes hat man bei konstanten niedri­geren Tempe­raturen Phasen­über­gänge. Aber über dem kritischen Punkt gibt es keine flüssige Phase mehr. Es gibt aller­dings eine Mög­lich­keit, einen Phasen­über­gang zu umgehen. Dazu muss man die Tempe­ratur jeweils anpassen und ober­halb der kritischen Tempe­ratur halten. Man umgeht damit den Zwei­phasen­bereich und hat trotz­dem die ganze Zeit eine flüssige Phase und bleibt ständig in einem ein­phasigen Gebiet.

Alternativ könnte man auch bei konstantem Volumen die Tempe­ratur und damit den Druck erhöhen. Wenn man das an der Stelle des kritischen Punkt durch­läuft, hat man die ganze Zeit über einen Zwei­phasen­bereich. Unten liegt die Flüssig­keit und ober­halb befindet sich das Gas, bis man schließ­lich den kritischen Punkt durch­stößt.

⇦ Kapitel Kapitel ⇨