Die Thermo­dyna­mik ist ein wichtiger Teil der Physik. Sie ermöglicht es, nicht nur Gase, sondern auch beliebige Körper in einer sehr grund­legenden Weise zu beschreiben.

Wir erinnern uns, dass sich zunächst einmal das betrach­tete ideale Gas bei geschlos­senem Ventil nur in dem Volumen V₁ befindet, und dort eine bestimmte Tempe­ratur hat. Das Gas breitet sich grund­sätz­lich über das ganze Volumen aus. Die Moleküle können unge­hindert durch das Ventil strömen und ver­ändern dadurch ihre innere Energie nicht. Da sich die mittlere Energie nicht ändert, bleibt auch die Tempe­ratur konstant. Wir erhalten damit letzten Endes einen Zustand, bei dem das Gas expandiert, von Volumen V₁ auf das Gesamt­volumen V, sich die Tempe­ratur dabei aber nicht ändert.

Die isotherme Expansion beim ersten Schritt des Carnot-Kreis­prozesses machte es erforder­lich, eine Wärme­menge zuzu­führen. Weil dieses System bei der isothermen Expansion auch eine Arbeit ver­richten soll. Beim Jouleschen Expansions­versuch wird aber keine Arbeit ver­richtet. Denn da bewegt sich ja nichts nach außen. Der Unter­schied liegt in der Rever­sibili­tät und Irre­ver­sibili­tät. Es wurde die Irre­ver­sibili­tät so definiert, dass Ände­rungen der Reihen­folge der äußeren Bedingungen dazu führen, dass sich auch der Vorgang umdreht. Das ist beim hin- und her­schieben eines Kolbens nach­voll­ziehbar. Das Gas expan­diert entspre­chend und kompri­miert wieder.

Diese isotherme Expansion und die sich daraus ergebende Wärme­zufuhr wurden in den vor­herigen Kapiteln mehr­fach heraus­gestellt:

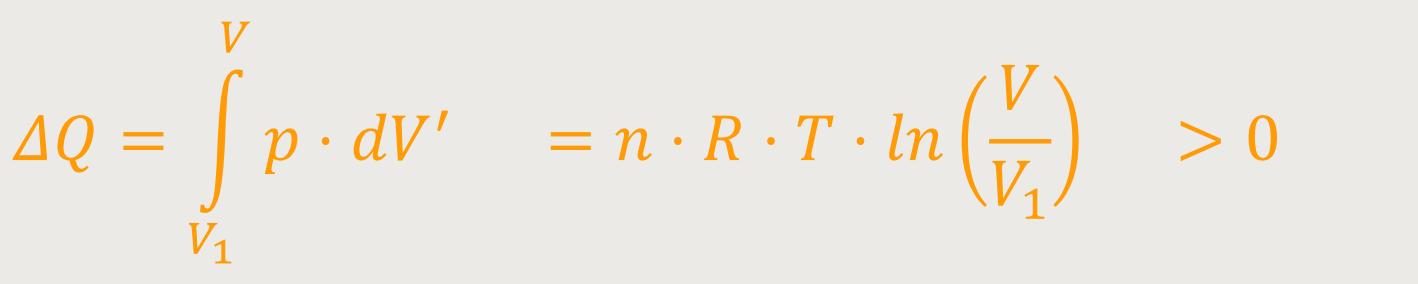
Von solchen irre­versiblen Prozessen sind wir ständig umgeben. So wie die Reibungs­kräfte und die konser­vativen Kräfte auch gang und gäbe sind. Hierbei muss man nur an die Gravi­tation rund um die Sonne denken. Dieses Kraft­feld ist in höchstem Maße ein konser­vatives Kraft­feld, sonst wäre unsere Erde nach vielen Milliarden Umkrei­sungen schon längst in die Sonne gefallen. Dieser Grad an Konser­vativi­tät des Gravi­tations­feldes in der Umgebung der Sonne und die Abwesen­heit irgend­welcher Reibungs­effekte, haben erst Leben auf der Erde ermöglicht. Wir können hierbei von einem außer­gewöhn­lich stabilen System sprechen.

Wie kann man dem Thema Entropie einen Sinn bzw. eine physika­lische Inter­pretation geben? Ludwig Boltzmann hat hier ganz entschei­dende Beiträge geleistet.

Die bisher betrachteten Aussagen muss man jetzt irgend­wie ver­stehen, und auch ver­suchen sie statis­tisch zu inter­pretieren. Es zeigt sich, dass der Weg zum Ver­ständ­nis dieser Aus­sagen im Wesent­lichen über die Statistik führt. Hierzu macht man wieder einen Schwenk, von der phäno­meno­logischen Thermo­dyna­mik mit ihren Haupt­sätzen, den Zustands­größen und deren Ände­rungen, zurück zur Statistik. Also zu dem, was wirk­lich in dem System abläuft.

Was bisher betrachtet wurde, sind Aus­sagen über statis­tische Mittel­werte. Wenn man von Tempe­raturen spricht, von Entropien oder von Wärme­zufuhren, dann spricht man eigentlich immer über Mittel­werte von Energien und Impulsen, sprich über viele, viele Moleküle in einem System.

Wenn man das zuvor Betrach­tete einiger­maßen nach­voll­ziehen will, muss man sich dessen bewusst sein, dass man es mit einem System sehr vieler Moleküle und dessen Dynamik zu tun hat. Um das explizit zu unter­suchen, muss man das Thema statis­tisch betrach­ten. Ziel ist es, dass vor allem dieser Begriff der Entropie physika­lisch anschau­licher wird. Und da beginnen wir wieder mit dem Jouleschen Expansions­versuch. Jetzt aller­dings wollen wir den gleichen Versuch statis­tisch betrachten.

Hierbei denken wir wieder an den Zylinder, diesmal mit schon geöffne­tem Ventil. Das Gas mit der Tempe­ratur T hat sich bereits über das gesamte Volumen V = V₁ + V₂ ausge­breitet. Und weil es sich um ein ideales Gas handelt, hat sich die Tempe­ratur nicht geändert. Jetzt wollen wir uns den Wahr­schein­lich­keiten W(V) und W(V₁) zuwenden:

Mit W wird die Wahr­schein­lich­keit für das Volumen V bezeichnet. Und zwar mit welcher Wahr­schein­lich­keit sich das Molekül im Volumen V befindet bzw. im Volumen V₁. Die Moleküle können sich frei in beiden Kammern bewegen. Die statis­tische Inter­pretation ist im Grunde etwas ganz Einfaches.

In unserem Gedanken­spiel gehen wir einmal davon aus, dass sich im Zylinder nur ein Molekül befindet. In dem Fall ist die Wahr­schein­lich­keit:

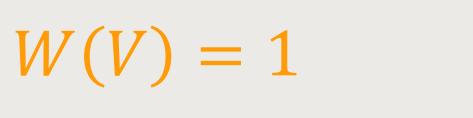
Die Wahr­schein­lich­keit für das Volumen V₁ ist entspre­chend:

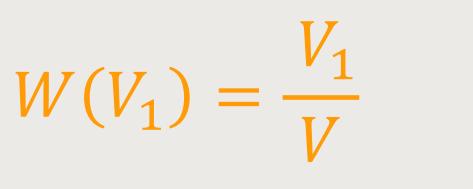
Man geht davon aus, dass sich das Molekül statisch chaotisch in dem Volumen bewegt, und weder Ort noch Geschwin­dig­keit zuein­ander korreliert sind. Man setzt quasi das molekulare Chaos voraus.

Was ist aber bei zwei Molekülen? In diesem Zusammen­hang muss man sich das Prinzip der Und-Wahrschein­lich­keit klar­machen. Die Wahr­schein­lich­keit, dass beide Moleküle im Volumen V sind, ist nach wie vor:

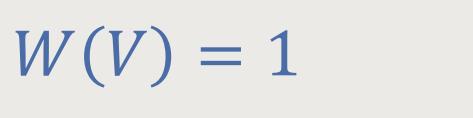
Aber, dass jetzt beide Moleküle im Volumen V₁ sind, bedeutet:

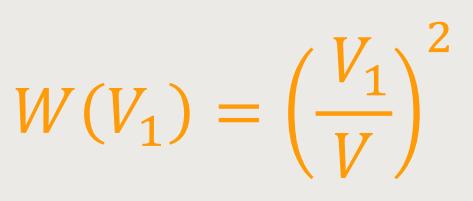
Dass zwei Dinge zur gleichen Zeit passieren, ist dann das Produkt der Wahr­schein­lich­keit. Die eine Wahr­schein­lich­keit multi­pliziert mit der anderen Wahr­schein­lich­keit.

Was ist aber, wenn das System N Moleküle hat? Also so viel Moleküle, wie zum Beispiel in 1 m³ Luft? Dann gilt nach wie vor:

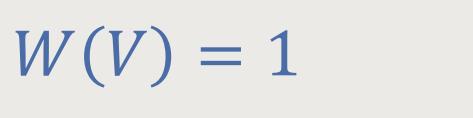
Dass sich jetzt alle Moleküle im Volumen V₁ befinden, bedeutet:

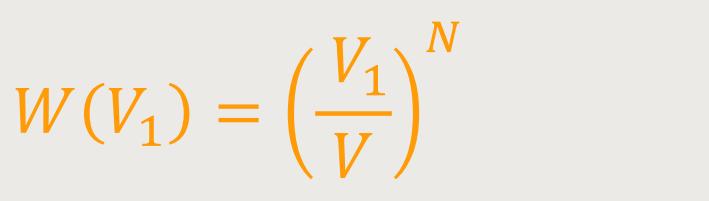
Und wenn man beispiels­weise annimmt, dass V₁ = V/2 ist, und dass N = 6 × 10²³ ent­spricht, dann ergibt sich daraus:

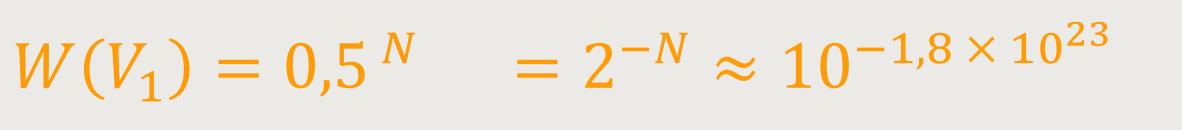
Die Wahr­schein­lich­keit ist so gering, dass sich alle Moleküle nur im Volumen V₁ befinden, dass dieser Zustand prak­tisch nie ein­treffen wird.

Jetzt könnte man denken, so eine Zahl kann man gedank­lich nicht wirk­lich erfassen. Boltzmann hatte sich davon jedoch nicht ab­schrecken lassen. Er versuchte, trotz dieser monströs kleinen Zahl, eine statis­tische Inter­pretation zu machen. Und wie so oft, machte auch er einen Ansatz für die Entropie:

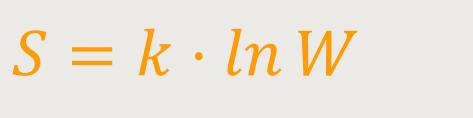
k   ist die Boltzmann-Konstante
W   ist die Wahrscheinlichkeit

In Verbindung mit der Tempe­ratur­definition wurde die Boltzmann-Konstante bereits beschrieben, als die mittlere kinetische Energie eines Moleküls pro Frei­heits­grad, also 1/2 · k · T. Hierbei steht das T für die makro­skopische Tempe­ratur.

Dieses ln W ist jetzt die Wahr­schein­lich­keit für den Zustand. Der natür­liche Logarithmus von einer sehr großen oder sehr kleinen Zahl ist schon über­schau­barer. Das ist im Wesent­lichen nur noch ein Exponent. Also nicht mehr 10¹⁰ · exp²³ sondern nur noch 10²³. Anschließend wird es multi­pliziert mit einer sehr kleinen Zahl k. Denn es geht ja um die mittlere kinetische Energie eines Moleküls pro Frei­heits­grad. Auf diese Weise erhält man etwas Über­schau­bares. Und das ist jetzt ganz einfach auszu­rechnen:

Jetzt lässt sich noch der Entropie­zuwachs ΔS berechnen. Also, die Ände­rung der Entropie zwischen dem Zustand, in welchem sich das gesamte System im Volumen V₁ befindet und dem Zustand, in welchem es sich in V = V₁ + V₂ befindet:

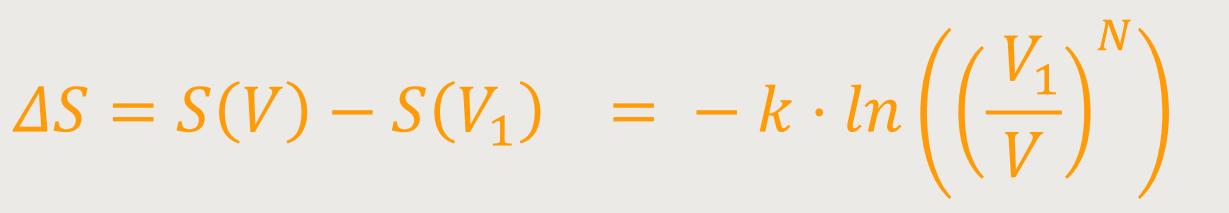
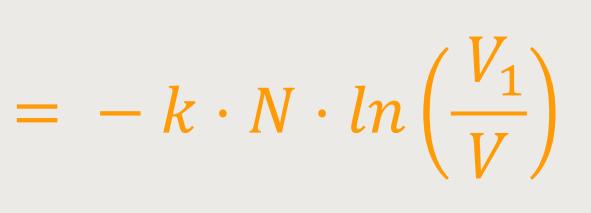
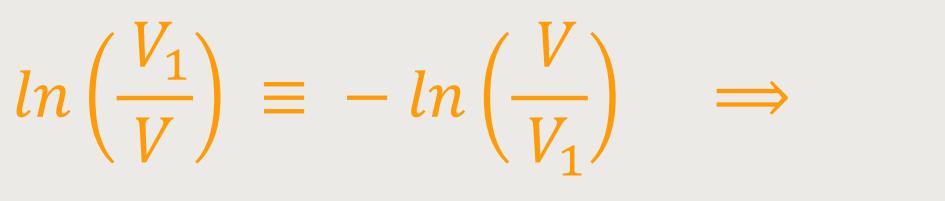
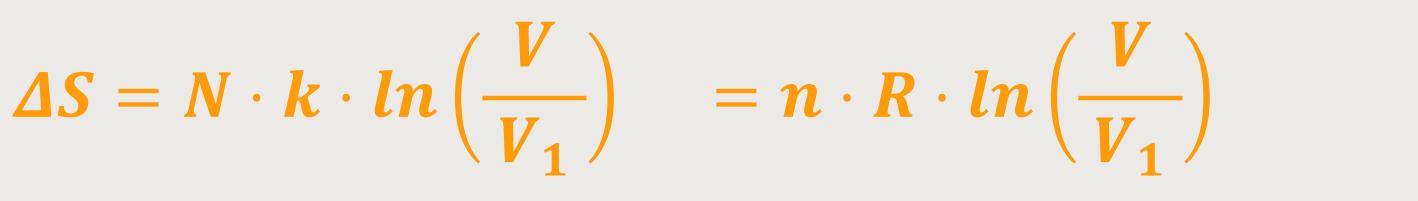
Diese statis­tische Über­legung führt zu einer Über­ein­stimmung mit den damals schon wohl­bekannten phäno­meno­logisch thermo­dyna­mischen Rela­tionen, mit denen seiner­zeit die Entropie ein­geführt wurde. Jetzt auf einmal erhält das Ganze eine Inter­pretation. Näm­lich, dass die Entropie etwas zu tun hat mit der Wahr­schein­lich­keit für das Auftreten eines Zustandes.

Diese Inter­pretation lässt sich noch etwas konkreti­sieren. Bis jetzt sind wir davon ausge­gangen, dass es um eine Wahr­schein­lich­keit W geht, zwischen 0 und 1, denn die Wahr­schein­lich­keit kann nicht > 1 sein. Aller­dings kann man dieses W auch anders inter­pretieren. Und zwar um einen gewissen, nicht unerheb­lichen Faktor größer, indem man es als die soge­nannte „Thermo­dyna­mische Wahr­schein­lich­keit” auffasst.

Diese Thermo­dyna­mische Wahr­schein­lich­keit ist nicht eine Wahr­schein­lich­keit im streng mathe­matischen Sinne, sondern eine Wahr­schein­lich­keit multi­pliziert mit einer konstanten Zahl. Man sagt auch, die Thermo­dyna­mische Wahr­schein­lich­keit ist die Anzahl der mikro­skopischen Realisie­rungs­mög­lich­keiten eines Makro­zustandes. Diese Anzahl kann sehr hoch sein.

Doch wenn man das Postulat der gleichen Apriori Wahr­schein­lich­keit annimmt, dann wird jede dieser einzel­nen mikro­skopischen Realisie­rungs­mög­lich­keiten, bei einem Makro­zustand gleich wahr­schein­lich auf­treten. Das bedeutet, je größer diese Thermo­dyna­mische Wahr­schein­lich­keit ist, desto größer wird die tat­säch­liche Wahr­schein­lich­keit für den Zustand. Wenn es viele Reali­sierungs­mög­lich­keiten gibt, und die alle gleich wahr­schein­lich sind, wird der Zustand insgesamt wahr­schein­licher sein, als wenn es nur eine einzige Reali­sierungs­mög­lich­keit gibt.

Man kann also die Wahr­schein­lich­keit W wieder als ein Maß für die Wahr­schein­lich­keit des Auf­tretens eines Makro­zustandes ansehen. Durch je mehr Mikro­zustände der Makro­zustand reali­siert werden kann, desto größer wird die Wahr­schein­lich­keit sein, dass er auch ein­tritt. Der Unter­schied zwischen den beiden Wahr­schein­lich­keiten ist nur ein konstanter Faktor. Da zusätz­lich ein Logarith­mus mit hinein­spielt bedeutet das, dass die Konstante nur additiv ist.

Bei der Entropie, wo es in erster Linie auf Ände­rungen ankommt, spielt eine additive Konstante genauso wenig eine Rolle, wie bei der poten­tiellen Energie. Dort geht es ja auch wieder nur um Energie­diffe­renzen. Und es hängt ledig­lich davon ab, was für einen Referenz­zustand man wählt. Also kann man letzt­lich dieselbe Inter­pretation aufrecht­erhalten, wenn man für die Wahr­schein­lich­keit eine Zahl nimmt, die die Anzahl der mikro­skopischen Reali­sierungs­möglich­keiten betrifft.

Das ist eine Zahl, die nie < 1 sein wird. Denn zumindest eine Reali­sierungs­möglich­keit wird wohl jeder Makro­zustand haben. Wenn man hypothe­tisch betrachtet einen Zustand direkt am absoluten Null­punkt hätte, lägen alle Moleküle geordnet herum und würden sich nicht bewegen. Diese Situation hätte im Wesent­lichen eine Reali­sierungs­mög­lich­keit, zumindest im klassischen Fall. Wenn man das quanten­mechanisch betrachtet, kann es noch zu Ent­artungen kommen.

Also, im Wesent­lichen ist dann die Wahr­schein­lich­keit = 1 und ln W = 0. Das heißt, in der Inter­pretation wird für den Fall, dass T → 0, auch S → 0 gehen.

Das bezeichnet man aus Sicht der phäno­meno­logischen Thermo­dyna­mik als den Dritten Hauptsatz.

Mit anderen Worten, am absoluten Null­punkt ist die Entropie Null. Oder bei Annähe­rung an den absoluten Null­punkt geht die Entropie gegen Null. Das ist eine will­kürliche Fest­legung des absoluten Betrages der Entropie. Der Rest verschiebt sich in entspre­chender Weise, sodass alles zusammen­passt.

Es wird ersicht­lich, dass obige Gleichung S(V₁) = k · ln (W(V₁)) zusammen mit der Inter­preta­tion für das W in allen Aspekten mit den drei phäno­meno­logischen Haupt­sätzen der Thermo­dynamik zusammen­passt. Daher kann es als eine sinn­volle statis­tische Inter­preta­tion des Begriffes der „Entropie” auf­gefasst werden. Die Entropie ist also ein Maß, für die Wahr­schein­lich­keit des Auf­tretens eines Makro­zustandes.

Für thermisch isolierte Systeme gelten somit:

Wenn man diese statis­tische Interp­reta­tion zugrunde legt, bedeutet das letzten Endes, dass sich bei Zustands­änderungen in thermisch isolierten Systemen die Zustände nur in Richtung größerer thermo­dyna­mischer Wahr­schein­lich­keit bewegen werden. Also Zustände, die ein größeres Chaos auf­weisen.

Das ist natür­lich weitest­gehend eine statis­tische Betrachtungs­weise. Denn in unserem Universum, einem weit­aus größeren makros­kopischen System, scheinen noch andere Gesetz­mäßig­keiten eine Rolle zu spielen. Andern­falls würde ein stetig zuneh­mendes Chaos zwangs­läufig zu einem Kollaps führen.

Dennoch ist es erkenn­bar, dass alle Lebe­wesen offene Systeme sind. Wir leben im wahrsten Sinne des Wortes vom Aus­tausch mit unserer Umgebung. Wir sind keine thermisch isolierten Systeme, weder thermisch noch massen­mäßig. Wir haben einer­seits eine thermische Wechsel­wirkung, und ander­seits haben wir einen Stoff­wechsel in beide Rich­tungen. Sonst können wir nicht existieren und andere Lebe­wesen auch nicht. Dieser Stoff­wechsel ist zudem eine Basis für unsere Existenz. Eine Ordnung geht immer auf Kosten der Umgebung.

⇦ Kapitel Kapitel ⇨